方程和方程组；不等式与不等式组复习：
考试目标:
方程和方程组
(1) 根据具体问题中的数量关系,列出方程或方程组 (b)
(2) 解一元一次方程和二元一次方程组 (c)
(3) 解可化为一元一次方程的分式方程(方程中分式不超过两个) (b)
(4) 用因式分解法、公式法和配方法解简单的数字系数的一元二次方程 (c)
(5) 用观察、画图或计算器等方法估计方程的解 (c)
(6) 根据具体问题的实际意义,检验结果是否合理 （b）
不等式与不等式组
(1) 不等式的意义 (a)
(2) 不等式的基本性质 (b)
(3) 解一元一次不等式及由两个一元一次不等式组成的不等式组,并在数轴上表示出解集 (c)
(4) 不等式及不等式组的简单应用 (c)
基本概念:
1.方程:含有未知数的等式叫做方程.
2.方程的解:使方程两边相等的未知数的值叫方程的解.
3.一元一次方程:只含有一个未知数且未知数的最高次数为一次的方程.
4.二元一次方程组:由两个只含有两个未知数的一次方程组成的方程.
5.不等式:用不等号连接起来的式子.(不等号有5种
)
6．一元二次方程的一般形式
，其中
分别是二次项系数，一次项系数和常数项。
7．分式方程的概念。
解题步骤：
1．一元一次方程的最简形式为:
一元一次方程的解题方法与步骤:去分母---去括号---移项-----合并同类项,化成最简形式----求解.
2．二元一次方程的解法:加减消元法;代入消元法.
3．不等式的性质:不等式两边都加上同一个数或式,所得不等式仍成立;不等式的两边都乘以或除以同一个正数,所得的不等式仍成立,不等式的两边都乘以或除以同一个负数,必须改变不等号的方向,不等式才成立
（1）。一元一次不等式的解题步骤一般如下：
去分母---去括号---移项-----合并同类项,化成最简形式求解.
 |
（2）。一元一次不等式组的解题步骤：
求出不等式组中每一个不等式的解------把每一个不等式的解表示在数轴上-------求出各不等式解的公共解。
4．解一元二次方程时，通常需把方程先整理成一般形式，然后选择因式分解法、配方法或公式法。
5．分式方程的解法关键是用去分母和换元法将其化为整式方程，了解分式方程产生增根的原因。
典型例题：
1．刘刚同学买了两种不同的贺卡共8张，单价分别是1元和2元，共用l 0元．设刘刚买的两种贺卡分别为x张、y张，则下面的方程组正确的是
A.
B．
c．
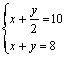D.
2．解方程组：
3．解方程
4．解一元二次方程
，结果正确的是
A、
B、
C、
D、
5．根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | －0.02 | 0.03 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是（ ▲ ）
A、3＜x＜3.23 B、3.23＜x＜3.24
C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
6．请聪明的你根据图中的对话内容，求出l本笔记本和1只钢笔各需要多少钱
7．
解不等式组：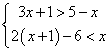
，并把解集在数轴上表示出来.
8．为节约用电，某学校于本学期初制定了详细的用电计划．如果实际每天比计划多用2度电，那么本学期的用电量将会超过2 530度；如果实际每天比计划节约2度电，那么本学期用电皱将会不超过2 200度．若本学期的在校时间按110天计算，那么学校每天用电量应控制在什么范围内?
巩固练习：
A
1.方程x(x+3)=x+3的解是 ( )
A. x=1 B. x1=0, x2=-3
C. x1=1, x2=3 D. x1=1, x2=-3
2. 方程x2-3x+2=0的解是 _______
3.解方程：
.
4.用配方法解一元二次方程x2-4x-1=O，配方后得到的方程是( )
A．(x-2)2=1 B．(x-2)2=4
C．(x-2)2=5 D．(x-2)2=3
5.解下列方程组：
6. 不等式组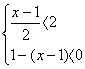
的解集是( )
A．2＜x＜5 B．0＜x＜5 C．2＜x＜3 D．x＜2
7. 如图4射线OC的端点O在直线AB上，∠AOC的度数比∠BOC的2倍多10°。设∠AOC和∠BOC的度数分别为x、y，则下列正确的方程组为…………（ ）
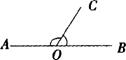A、
B、
C、
D、
8. 若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程是：
A、
， B、
，
C、
， D、
；
9. 某酒店客房部有三人间、双人间客房，收费数据如下表．
| 普通(元/间／天) | 豪华(元/间／天) | |
| 三人间 | 150 | 300 |
| 双人间 | 140 | 400 |
为吸引游客，实行团体入住五折优惠措施．一个50人的旅游团优惠期间到该酒店入住，住了一些三人普通间和双人普通间客房．若每间客房正好住满，且一天共花去住宿费1510元，则旅游团住了三人普通间和双人普通间客房各多少间？
10．不等式组
的最小整数解是（
）
A．－1 B.0 C.2 D.3
B
1.用换元法解方程
―
+6=0，如果设y=
，那么原方程可变形为 ．
2.如果-4是关于x的一元二次方程2x2+7x-k=0的一个根，则k的值为 ．
3.某校学生暑假乘汽车到外地参加夏令营活动，目的地距学校120km。一部分学生乘慢车先行,出发1h后，另一部分学生乘快车前往，结果他们同时到达目的地。已知快车速度是慢车速度的1.5倍,如果设慢车的速度为
,那么可列方程为（ ）
A.
－
B.－
C.
D.
4. ⊙O的半径OA=2，弦AB、AC的长分别为一元二次方程x2-(2
+2
+4
=0的两个根，则∠BAC的度数为 ．
5.如果关于
的方程
的解也是不等式组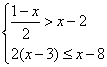
的一个解，求
的取值范围。
6.解方程：
．
7.关于的不等式3一2
≤一2的解集如图所示，则的值是_______________。
8. 为了加强学生的交通安全意识，某中学和交警大队联合举行了“我当一日小交警”活动，星期天选派部分学生到交通路口值勤，协助交通警察维护交通秩序．若每一个路口安排4人，那么还剩下78人；若每个路口安排8人，那么最后一个路口不足8人，但不少于4人．求这个中学共选派值勤学生多少人？共有多少个交通路口安排值勤？
9. 不等式组
的整数解是 。
10.如果
，那么代数式
的值为…………………………（ ）
A、6 B、8 C、—6 D、—8
C
1.
求不等式组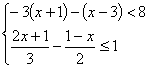
的解集
2.
，求A、B的值。
3. 已知一元二次方程x2-4x+k=0有两个不相等的实数根
(1) 求k的取值范围;
(2) 如果k是符合条件的最大整数，且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根，求此时m的值.
4.一个矩形，两边长分别为xcm和10cm，如果它的周长小于80cm，面积大于100cm2．求x的取值范围．
5. 下列命题是真命题的是
A、
=
B、今天下雨的概率是0
C、
可推出
D、
6. 张大叔从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为15米3的无盖长方体运输箱，且此长方体运输箱底面的长比宽多2米，现已知购买这种铁皮每平方米需20元，问张大叔购回这张矩形铁皮共花了多少元钱？
7.某商场试销一种成本为60元/件的T恤，规定试销期间单价不低于成本单价，又获利不得高于40%，经试销发现，销售量
（件）与销售单价（元/件）符合一次函数
，且
时，
；
时，
；
（1）求出一次函数的解析式；
（2）若该商场获得利润为
元，试写出利润与销售单价之间的关系式，销售单价定为多少时，商场可获得最大利润，最大利润是多少？
8. 某电脑公司现有A，B，C三种型号的甲品牌电脑和D，E两种型号的乙品牌电脑．希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑．
(1) 写出所有选购方案(利用树状图或列表方法表示）；
(2) 如果(1)中各种选购方案被选中的可能性相同，那么A型号电脑被选中的概率是多少？
(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示)，恰好用了10万元人民币，其中甲品牌电脑为A型号电脑，求购买的A型号电脑有几台．
9．.某夏令营的活动时间为15天，营员的宿舍安装了空调。如果某间宿舍每天比原计划多开了2个小时的空调，那么开空调的总时间超过150小时；如果每天比原计划少开了2个小时的空调，那么开空调的总时间不足120小时，问原计划每天开空调时间为多少小时？
10. 由于电力紧张，某地决定对工厂实行鼓励错峰用电．规定：在每天的7:00至24:00为用电高峰期,电价为元/度；每天0:00至7:00为用电平稳期,电价为
元/度．下表为某厂4、5月份的用电量和电费的情况统计表：
| 月份 | 用电量（万度） | 电费（万元） |
| 4 | 12 | 6.4 |
| 5 | 16 | 8.8 |
(1)若4月份在平稳期的用电量占当月用电量的
，5月份在平稳期的用电量占当月用电量的
，求、 的值．
(2)若6月份该厂预计用电20万度，为将电费控制在10万元至10.6万元之间（不含10万元和10.6万元），那么该厂6月份在平稳期的用电量占当月用电量的比例应在什么范围？