初三数学竞赛试题

　　　　　　　　　　　　  　　　班　　　　 姓名　　　　

一、选择题：(每小题5分,共30分)

 1．已知n是奇数，m是偶数，方程组　　　　　　  有整数解（x₀，y₀）则∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（　　 ）

A、x₀，y₀均为偶数　　　　　　　　　　　 B、x₀，y₀均为奇数

C、x₀为偶数，y₀为奇数　　　　　　　　　 D 、y₀为偶数，x₀为奇数

2．若ab≠0,则等式　　　　　　　　　 成立的条件是∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（　　）

A、a>0,b>0　 B.a<0,b>0　 C. a>0,b<0　　 D. a<0,b<0

3.设a,b,c,d都是非零实数，则-ab,ac,bd,cd∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ (　  )

A、都是正数　　B、都是负数　　C、是两正两负　 D、是一正三负或一负三正

4．如果某商品进价降低5%而售价不变，利润率（利润率=）可由目前的a%增加到（a+15）%，则a的值∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（ 　 ）

A、185　　　　 B、175　　　　  C、155　　　　D、145

5．若x₀是一元二次方程ax²+x+c=0(a≠0)的根，则判别式△=b²-4ac与平方式M=（2ax₀+b）²的大小关系是∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙（　　）

A、△=M　　  B、△>M　　　　C、△<M　　  D、不能确定

6．用四条线段a=14，b=13，c=9，d=7作为四条边构成一个梯形，则在所构成的梯形中，中位线的长的最大值是∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ （　　）　

A、13．5　　　B、11.5　　　 C、11　 　　 D、10.5

二、填空题(每小题5分,共30分)

7．已知则m+n的值是　　　　.

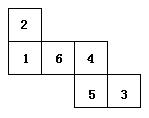8.一个均匀的立方体的六个面上分别标有数1，2，3，4，

5，6.右图是这个立方体的侧面展开图.抛掷这个立方体,

则朝上一面的数恰好等于朝下一面上的数的的概率

是　　　　　 .

9.己知a,b是方程x²-4x+m=0的两根，b,c是方程x²-8x+5m=0的根.m=　　  .　　　　　

10.若x₁、x₂都满足条件∣2x-1∣+∣2x+3∣=4,且x₁<x₂,则x₁-x₂

的取值范围是　　　　　　  .

11.如图，在圆内接四边形ABCD中，∠A=60°，∠B=90°，

AB=2，CD=1，则BC=　　　　　　 .　　　　　　　

12 ..如图，OA=,AB=1的矩形OABC在直角坐标

系中，将矩形OABC沿OB对折，点A落在点A^’，

则点A^’的坐标是　　　　　　　 .　　　　 

三、解答题(每小题15分,共60分)

13. 已知关于x的方程

（1）　　求证：无论k取何实数值，方程总的实数根；

（2）　　若等腰三角形ABC的一边长a=6，另两边长b、c恰好是这个方程的两个根，求此三角形的周长。

 

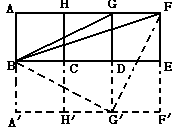
14．如图，已知3个边长相等的正方形相邻并排。

求∠EBF+∠EBG.

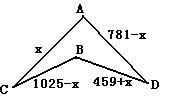
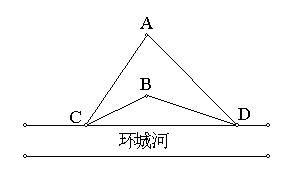15．城区某环城河道进行整理，如图，在C段

和D段河岸需要土方数分别为1025方和1390方，

现离河道不远有两建筑工地A和B分别需运走土

方数是781方和1584方，利用这些土先填满河岸

C段，余下的土填入河岸D段.已知每方土运费：

从A处运到C和D段分别是1元和3元；从B处

运到C段D和段，分别是0.6元和2.4元.问怎

样安排运土，才能使总费用最少，并求出总运费的值.

16．从1，2，3，┅，2004中任选k个数，使所选的k个数中，一定可以找到能构成三角形边长的3个数（这里要求三角形三边长互不相等）.试问：满足条件的k的最小值是多少？

参考答案:

一、CBDAAD；

二、7．0；由已知条件知(m+n)²+p²=0；8.；因为只有3的对面是6，所以3在上面的概率是；9. 0或3，因为两方程有一个共公根b；10. -2≤x₁-x₂<0，同解不等式只能相加；11.-2；延长AD、BC构成含30⁰的直角三角形；

12. 过A₁作x轴、y轴的垂线，利用含30⁰的直角三角形求得（）.

13. （1）、证明△≥0即可；

（2）、从a=6是腰或底两种情况讨论得16或22  .

14. 解法1：如图将已知3个边长相等的正方形

以BE为轴进行翻折，连结BG^/，FG^/，设AB=a

则有∠EBG=∠EBG^/

∠EBG+∠EBF=∠EBG^/+∠EBF=∠FBG^/

又BG^/2=a²+(2a)²=5a²

FG^/2= a²+(2a)²=5a²,BF²=a²+(3a)²=10a²

所以BG^/2+ FG^/2= BF²

∠FBG^/=45⁰　 ∠EBG+∠EBF=45⁰.

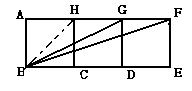
解法2：如图连结BH，证△BHG∽△FHB

∠HBG=∠HFB, ∠HGB=∠HBF得证.　　

15.如图所示，设从A运到C是x方，总运费为y元，

则从A运到D是（781-x）方，从B运到C

是（1025-x）方，从B运到D是（459+x）方，

故，y=x+3（781-x）+0.6（1025-x）+2.4（459+x）(0≤x≤781)

从A运到C、D土方数分别是781、0方；

从B运到C、D土方数分别是244、1340方，

运费最少为4143.4元.

16.这一问题等价于:在1,2,┅2004中选k-1个数,

使其中任意3个数都不能成为一个三角形三边(互不相等)的长.试问满足这一条件的k的最大值是多少?

符合条件的数组中,

当k=4时,最小的3个数是1,2,3.不能构成三角形,由此可不断扩大该数组:1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597共16个数,只有在这16个数中,任何三个数不能构成三角形,故n≤16≤k-1从而，k≥17.