初三数学
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 总分 | 累分人 | 座位号 | ||
| 得分 | |||||||||||
说明：本卷共有六个大题、25个小题，全卷满分120分，考试时间为120分钟.
| 得分 | 评卷人 |
一、填空题（本大题共10小题，每小题3分，共30分）
1、计算：-4-4÷4= .
2、一块正方形地砖的面积为0.09平方米，则其边长是 米.
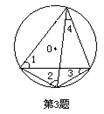
3、如图，在圆内接四边形中，则∠1+∠2+∠3+∠4= 度.
4、一本练习本的价格是a元，
则50a元可以解释为： .
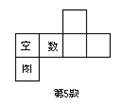5、如图，在正方体展开图中填上合适的字，使正方体相对
的面中的两字恰好组成一个词语.
6、在函数y = -
的图象上，横、纵坐标均为整数的点的
坐标是 .
7、试写出一个以y轴为对称轴的二次函数解析式： .
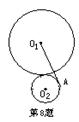8、如图，⊙O1和⊙O2外切，它们的半径分别是3和1，
过O1作⊙O2的切线，切点为A，则O1A长为 .
9、有一拦水坝的横截面是梯形，已知该堤坝的迎水坡的坡度
为1：
，背水坡的坡度为1：2，那么迎水坡、背水坡的
坡角分别是
度.
（tan26.56°=0.5, tan63.4°=2, sin30°=0.5, cos63.4°=0.5）
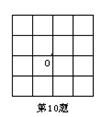
10、在4×4的正方形网格中，以O为圆心，画两个同心圆，
使小⊙O的面积等于大⊙O的面积的一半.
| 得分 | 评卷人 |
二、选择题(本大题共6小题,每小题3分,共18分)
每小题只有一个正确选项,请把正确选项的代号填在题后的括号内.
11、计算（-1）-1+（-1）0结果正确的是 [ ]
A 0 B 1 C –1 D 2
12、据报道：2005年10月12日9时，从我国“神舟”六号载人飞船升空到17日4时32分安全返回地面，其间飞船飞行的路程约为325万千米，共花时间约115.5小时，则“神六”飞船平均每小时约飞行（结果保留二个有效数字）[ ]
A 2.8×105千米 B 2.8×104千米
C 2.81×104千米 D 3×105千米
13、已知k＞0, b＜0 , 则直线y=kx+b 不经过的象限是 [ ]
A 第1象限 B 第2象限 C 第3象限 D 第4象限
14、关于分式 ，下列说法不正确的是 [ ]
A 当x=0时，分式没有意义 B 当x＞5时，分式的值为正数
C 当x＜5时，分式的值为负数 D 当x=5时，分式的值为零
15、设m,n是方程x2-2006x-1=0的两根，则代数式m(n+1)+n的值是 [ ]
A –2005 B 2005
C –2007 D 2007
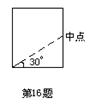16、如图，在矩形纸片中，按虚线剪开后，将两部分进行拼接，则下列四个图形中，不能拼出的是
[ ]
A 直角三角形 B 等腰梯形
C 菱形 D正方形
| 得分 | 评卷人 |
三、（本大题共3小题，第17题6分，每18、19题均为7分，共20分）
17、当m，n为互不相等的正数时，分式m+n-
的值是正还是负？试说明你的理由.
18、已知不等式①x-3＜0 , ②1＞3-x , ③
-x ＜
，从这3个不等式中任取两个构成不等式组，其中是否存在一个解集中只有一个整数解的不等式组？若存在写出不等式组并求这个整数解，若不存在请说明理由.
19、小明想了解12岁以上吸烟人数的分布情况，于是他随机对120名吸烟者进行了调查，下面是他收集的有关数据后制成的统计表：
| 年龄段x（周岁） | 12≤x≤18 | 19≤x≤24 | 25≤x≤39 | X≥40 |
| 人数（人） | 3 | 24 | 45 |
（1）补填上表空白；
（2）按表中各年龄段的吸烟人数的比例将⊙O分成4个扇形（要求：要注明圆心角度数），并简述此图对了解吸烟人数的分布有何作用？
| 得分 | 评卷人 |
四、(本大题共2小题，每小题8分,共16分)
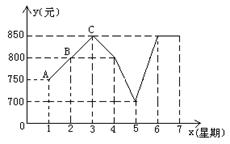20、某文具店一周内的销售额情况如图所示：
（1）试求该文具店一周内的日平均销售额，
并用这个样本平均数估计该店一月（30天）
的销售额；
（2）从图中A、B、C三点中选两点求出经过
这两点的一次函数解析式，判断第三点是否在图象上？
（3）观察图象写出你从图象中获取的两个信息.
21、观察下列各式：
①
－
， ②
－
，③
－
，④
－
…
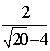（1）化简以上各式其结果依次为： －1 ，－2 ， ， ；
（2）以上各式及对应的结果存在一定规律，请你按照这个规律写出第5个式子及结果： ；
（3）用含n（n ≥1的整数）的式子写出第n个式子和它的结果，并给出化简过程.
| 得分 | 评卷人 |
五、(本大题共2小题，第22题8分，第23题9分,共17分)
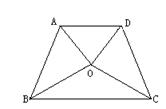22、在梯形ABCD中，O是梯形内部一点，且OA=OD ，OB=OC，当O是对角线的交点时，易证△AOB≌△COD，即可得梯形ABCD是等腰梯形，当O不是对角线交点时（其它条件不变），梯形ABCD还是等腰梯形吗？试证明你的结论.
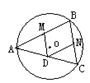
23、如图，A、B、C为⊙O上的三点，D、M、N分别是AC、AB、BC的中点，
（1）求证：四边形BNDM是平行四边形；
（2）若点A固定，B、C在圆周上运动（不一定同时动），同时D、M、N的位置也相应改变（D、M、N为三边的中点不变），试探究由点B、C怎样的位置，分别可得到四边形DMBN是：菱形、矩形、正方形，并选择其中一种情况给予证明.
| 得分 | 评卷人 |
六、(本大题共2小题，第24题8分，第25题9分,共19分)
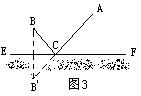24、如图，EF是一条笔直的河岸，A村与B村相距4千米，A、B两村到河岸EF的距离分别是5千米、3千米，现要在河岸EF上选一地址C建一个自来水厂，并铺设水管把水引至A、B两村.
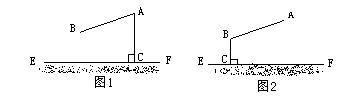
AC⊥EF于C BC⊥EF于C B与B’关于EF对称，AB’交EF于C
（1）问：如图1、2、3所示的三条铺设水管的路径（图中实线部分）哪条最短？并说明其理由；
（2）若铺设水管的路径是图2中的实线，经预算铺设水管的材料费和铺设工资总共为116万，已知BC段的每千米材料费是AB段每千米材料费的
倍，但AB段与BC段每千米的铺设工资相同，又知BC段每千米两种费用的和为20万元（不考虑其他因素），求BC段材料费和铺设工资各为多少万元？
25、如图，在直角坐标系中，A（0，-4），B（-12，-4），C（-12，0）若用一块三角板的直角顶点E（n,-4）沿着线段AB滑动，在滑动的过程中一条直角边始终经过点C，另一条直角边与y轴交点P(0,m).
（1）当CE平分∠OCB时，求点P的坐标；
（2）问点E滑到何处时，Rt△CPE中有一个内角为30度？
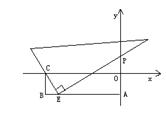（3）在上述三角板的滑动过程中，试求m与n之间的函数关系式,并探究点P坐标是否有为（0，6）和（0，1）的情形？若有，求出相应的点E的坐标,若没有，说明其理由.
参考答案与评分
一、填空题(本大题共10小题,每小题3分,共30分)
1、-5；2、0.3；3、180；4、50本练习册的费用；5、如
6、（-1，1），（1，-1）； 7、如：y = x2 ；8、
；9、300，26.560；
10、都以O为圆心，分别以小正方形的边长，对角线为半径的两圆（答案不唯一）.
二、选择题(本大题共6小题,每小题3分,共18分)
11、A 12、B 13、B 14、C 15、B 16、D
三、(本大题共3小题,第17小题6分,第18、19小题各7分，共20分)
17、解：原式= ，…………………………4分
∵m﹥0,n﹥0,m≠n,分式的值为正数…………………………6分
18、解：存在，…………………………2分
∵①x﹤3 ②x﹥2 ③ x﹥1…………………………3分
∴由此观察可知：①与③组成不等式组满足条件，解集为1﹤x﹤3,这个整数解为x=2.
…………………………7分
19、解：（1）48. …………………………3分
（2）四个扇形的圆心角分别是90，720，1440，1350. …………………………5分
作用：能清楚地表示各部分在总体中所占的百分比. …………………………7分
四、(本大题共2小题，每小题8分,共16分)
20、解：（1）
=800，800×30=24000（元）。
…………………………3分
（2）直线AB的解析式为y=50x+700,点C在AB上 . …………………………6分
(3)如：星期五销售额最低仅700元，或双休日销售额较高. …………………………8分
21、解：（1）-3，－4 。…………………………2分
（2）
- 
= -5…………………………5分
（3） …………………………6分
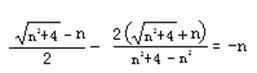
化简过程： …………………………8分
五、(本大题共2小题，第22题8分，第23题9分,共17分)
22、解：是等腰梯形. …………………………2分
简证：过O作EF∥AD，先证∠AOB=∠DOC，再证：△ABO≌△DCO，可得AB=DC。
…………………………8分
23、（1）略证：∵D、M、N分别是AC、AB、BC的中点 ，
∴DM∥BN，DN∥BM，四边形MDNB是平行四边形. …………………………3分
(2)当AC为非直径弦，B为弧ABC的中点时，四边形DMBN是菱形；
当AC为直径，B不是弧ABC的中点时，四边形DMBN是矩形；
当AC是直径，B是弧ABC的中点时，四边形DMBN是正方形. …………………………8分
如：第1种情况证明：∵B为弧ABC的中点，AB=BC，M，N分别是AB、BC的中点，
∴BM=BN，四边形DMBN是平行四边形。
∴平行四边形DMBN是菱形. …………………………9分
六、(本大题共2小题，第24题9分，第25题10分,共19分)
24、解：（1）图1：4+5=9 ，图2：3+4=7，图3：BC=B’C,
过B’作B’M∥EF,过A作AN∥BB’交于D，则构成直角三角形ADB’.B’D=2,
∴AB’=
∴
﹥﹥
. ∴图2的路径最短. ……………4分
(2)设BC段材料费每千米X万元,铺设工资每千米y万元
x+y=20
3(x+y)+4(
x+y)=116，…………………………6分
∴x=18,y=2。…………………………8分
BC段材料费为54万元,铺设工资为6万元. …………………………9分
25、解：(1)当CE平分∠OCB时，BC=BE=4 .
∴AE=AP=12-4=8. 8=m+4，m=4∴P(0,4) …………………………3分
(2)当∠CPE=300时，PE：CE=
：1，又∵易证：△CBE∽△EAP，AE= -n ，
=
∴n =-4
∴当∠PCE=300时，=
， n =-
…………………………4分
∴当E（-4，-4）或（-
，-4）时，满足Rt△CPE内一角为300. ……………7分
(3)∵△CBE∽△EPA，AE= -n ,AP=m+4, EB=n+12，
=
， m= - 
n2-3n-4
设点P坐标为（0，6），则6= -
n2-3n-4 ， △=144-160﹤0，
点（0，6）不能是P 点（或抛物线m =-(n+6)2+5）,最高点为（-6，5），
即m的值不会大于5）.1= -
(n+6)2+5 ，
n1 = -10, n2 = -2, 点P的坐标可以是（0，1），
此时E为（-10，-4）或（-2，-4）. …………………………10分