衢州市菁才中学2005年中考模拟试卷(二)
数 学 05.6.2
考生须知:
1. 全卷满分为150分,考试时间为120分钟。
2. 请用蓝、黑色钢笔或圆珠笔在试卷密封区内填写班级、姓名、学号、试场号和座位号。
3. 答题时请注意解题过程不要写到密封线内。
4. 答题时允许使用不带存储功能的计算器。
试卷Ⅰ
一. 选择题(本题共12小题,每小题4分,共48分.请选出各题中一个符合题意的正确选项,不选、多选、错选均不给分,答案须填写到答题卷相应位置上)
1.如果水库的水位高于正常水位2米时,记作+2米,那么低于正常水位3米时,应记作 ( )
A.+3米 B.-3米 C. +![]() 米 D. -
米 D. -![]() 米
米
2.下列运算中,计算结果正确的是 ( )
A.a4 ·a3=a7 B.a6÷a3=a2 C.(a3)2=a5 D.2a+3b=5ab
3.用换元法解方程![]() ,设
,设![]() ,则原方程可化为 ( )
,则原方程可化为 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D.
![]()
4.用一把带有刻度的直角尺,
①可以画出两条平行的直线![]() 与
与![]() ,如图(1);②可以画出∠AOB的平分线OP,如图(2);
,如图(1);②可以画出∠AOB的平分线OP,如图(2);
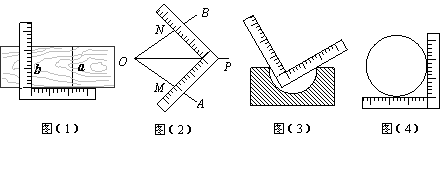 ③可以检验工件的凹面是否成半圆,如图(3);④可以量出一个圆的半径,如图(4).
③可以检验工件的凹面是否成半圆,如图(3);④可以量出一个圆的半径,如图(4).
上述四个方法中,正确的个数是( )
(A)1个 (B)2个 (C)3个 (D)4个
5. 如图表示某个不等式的解集,该解集中所含的自然数解的个数是 ( )
A.3个 B. 4个 C. 5 个 D. 6个
6.如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
7. 已知一次函数y=kx+b的图象经过第一、二、四象限,则反比例函数y=![]() 的图象在( )
的图象在( )
A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限
8.向如图所示的容器内注水, 则水对容器底部的压强P与水深h的函数图像是( )
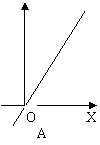 | 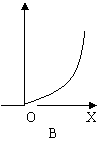 | 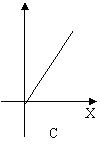 | 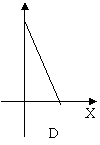 | ||||||
 | |||||||||
|
|
|
|
|
|
9. Rt△ABC中, ∠C=Rt∠, tanA=![]() ,则sinA的值是( )
,则sinA的值是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
10. 已知△ABC中,AB=4, AC=3, BC=6. D是AC上一点且AD=1, P在AB上,若连结PD,
△APD与△ABC相似,则AP长为( )
A. ![]() B.
B. ![]() C.
C.
![]() 或
或![]() D. 1或4
D. 1或4
11. 半径之比为3:4的两圆外切时, 圆心距为14, 则两圆内切时,圆心距d应满足( )
A. d=2 B. d=1 C. d>2 D. 1<d<2
12. 设f(x)=x2-x+2 (f(x)表示关于x的函数, 如f(o)=o2-o+2=2, f(m)=m2-m+2, 若m≠n,有f(m)=f(n)=a, 则f (m+n)= ( )
A. 1 B. –1 C. 2 D. 2a
二. 填空题(每题5分,共30分)
13. 分解因式 a3-a=__________
![]() 14. 小明设计了一个实数运算的程序: 输入一个数后,输出的数总比该数的平方多3, 小刚按此程序输入-2
14. 小明设计了一个实数运算的程序: 输入一个数后,输出的数总比该数的平方多3, 小刚按此程序输入-2![]() 时, 则输出的结果是_______________
时, 则输出的结果是_______________
15.写出一个含有字母![]() 的分式(要求:不论
的分式(要求:不论![]() 取任何实数,该分式都有意义,且分式的值为负)
.
取任何实数,该分式都有意义,且分式的值为负)
.
16. 用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= 度.
 | |||||
 | |||||
| |||||
17. 观察下面各组数(3, 4, 5) (5, 12, 13), (7, 24, 25)…发现32=4+5,52=12+13, 72=24+25,…请另写一组具有以上规律的一组数(_____ _____ _____ )若数组中第一个数表示为k,第二个数表示为n,请用k的代数式表示n:______________
18.△ABO中,OA=OB=5, OA边上的高线长为4, 将△ABO放在平面坐标系中,使O与原点重合,点A在x轴的正半轴上,那么点B的坐标是_____________
试卷II
19. (8分) 计算: ![]() 20.(8分) 解方程
20.(8分) 解方程 ![]()
21. (9分)有一种窗框设计采用一个正方形内接在一个半圆中的图形组成,设半圆的直径AB=2.
(1)求正方形的边长;
(2)试证明点C是线段AD的一个黄金分割点.
22.(本题满分9分)
根据对全国31个省(区、市)68000个农户的抽样调查,一季度,农民人均现金收入(包括工资性收入、出售农产品收入、生产经营收入和财产性、转移性现金收入)比上年同期有明显增长. 其中三项现金收入人均增长数额占一季度人均现金收入增长数额的百分数如图所示,而出售农产品收入增加最多,达44元.
(数据来源:国家统计局2004-04-27)
 请根据以上信息回答下列问题:
请根据以上信息回答下列问题:
(1)一季度农民人均现金收入增加了多少元(精确到1元)?
(2)农民人均生产经营收入增加了多少元(精确到1元)?请在图中相应的位置画出示意图,并标注所占的百分数.
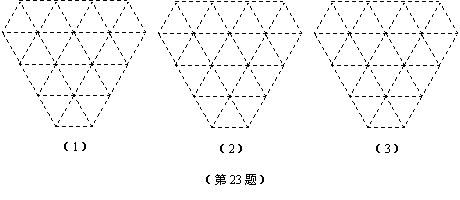
23.(本题满分12分)
请你在下面3个网格(两相邻格点的距离均为1个单位长度)内,分别设计1个图案,要求:在(1)中所设计的图案是面积等于![]() 的轴对称图形;在(2)中所设计的图案是面积等于2
的轴对称图形;在(2)中所设计的图案是面积等于2![]() 的中心对称图形;在(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3
的中心对称图形;在(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3![]() .将你设计的图案用铅笔涂黑.
.将你设计的图案用铅笔涂黑.
 |
|
|
|
|
 厘米/秒的相同速度沿BC,
CA向C, A运动,连结PQ交AD
厘米/秒的相同速度沿BC,
CA向C, A运动,连结PQ交AD
于M, 设P、Q运动的时间为t秒;
|
|
(1)t为何值时,以点D、M、P组成的三角形与△ABD相似;
(2)设△PDM的面积为S, 请写出S关于t的解析式,并求出S的最大值或最小值.
(3)直接写出线段QM,线段PM的大小关系。(不必写证明过程)
25. (本题14分)
在直角坐标系中, 抛物线y=x2+mx-![]() m2(m>0) 与x轴交于A, B两点,若A,B两点到原点的距离为OA, OB, 且满足
m2(m>0) 与x轴交于A, B两点,若A,B两点到原点的距离为OA, OB, 且满足![]()
(1) 求m的值.
(2) 若抛物线与y轴交于点C, 过A, B, C三点作
圆M, ⊙M与y轴交于C, D两点,求经过点D的⊙M的切线解析式.
(3) 问过点D的⊙M切线与过点A的⊙M切线是否垂直,若垂直,
写出证明过程,若不垂直,试说明理由.
