初三数学模拟试题

2014-5-11 0:17:57 下载本试卷

2006届初三数学模拟试题

题

号

一

二

三

1~10

11~15

16

17

18

19

20

21

22

得

分

一、选择题（本大题共10小题，每小题3分，共30分）

每小题给出4个答案，其中只有一个是正确的．请把正确答案的字母代号填在下面的答题表一内，否则不给分．

题号

1

2

3

4

5

6

7

8

9

10

答案

1．4的平方根是(　　)

　 A．2　　　　B．±2　　　　C．-2　　　　D．±

2．据2004年《黄石年鉴》记载，2003年全市财政收入元，用科学计数法表示为(　　)

　 A．1.905×109元　　B．1.905×1010元　　 C．1.905×1011元　 D．1.905×1012元

3．下列计算结果正确的是　　　

A、　　 B、=　　C、　 D、　　

4．有一实物如图，那么它的主视图　　　　　　　　　　　　　　　　　　　　　 （　　）


A　　　　　　　 B　　　　　　　  C　　　　　　  D

5、不等式组的解集在数轴上可表示为（　）

　A、　　 B、　

C、　　　D、

6、下列事件中：确定事件是（　）

　 A、掷一枚六个面分别标有1~6的数字的均匀骰子，骰子停止转动后偶数点朝上

　 B、从一副扑克牌中任意抽出一张牌，花色是红桃

　 C、任意选择电视的某一频道，正在播放动画片

　 D、在同一年出生的367名学生中，至少有两人的生日是同一天。

7、下面有4个汽车标致图案，其中是轴对称图形的是

①　　　　　　　 ②　　　　　　　 ③　　　　　　  ④

A、②③④　　　　B、①③④　　　　C、①②④　　　　D、①②③

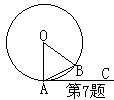8．如图，A、B是⊙O上的两点，AC是⊙O的切线，∠B=65º，则∠BAC=（　　 ）

　 A、35º　　　　　　B、25º　　　　　　

　 C、50º　　　　　　D、65º

9．已知Rt△ABC的斜边AB=5，一条直角边AC=3，以直线BC为轴旋转一周得到一个圆锥，则这个圆锥的侧面积为（　　 ）

　 A、8π　　　　　　B、12π　　　　　

　 C、15π　　　　　 D、20π

10．如图，E，G，F，H分别是矩形ABCD四条边上的点，EF⊥GH，若AB＝2，

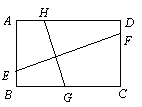BC＝3，则EF︰GH＝　　

（A） 2︰3　　　　

（B） 3︰2　　　　

（C） 4︰9　 　　　

（D） 无法确定　　

二、填空题（本大题共5小题，每小题3分，共15分.请将答案填在答题表二内相应的题号下.否则不给分）

题号

11

12

13

14

15

答案

11．因式分解：=________。

15．下表是某摩托车厂今年1至5月份摩托车销售量的统计表：（单位：辆）

月份

1

２

３

４

５

销售量（辆）

1700

2100

1250

1400

1680

则这5个月销售量的中位数是　　　　　　　辆．

13．“五一”黄金周期间，梁先生驾驶汽车从甲地经过乙地到丙地游玩．甲地到乙地有2条公路，乙地到丙地有3条公路．每一条公路的长度如下图所示(单位：km)．梁先生任选一条从甲地到丙地的路线，这条路线正好是最短路线的概率是　　　　 ．


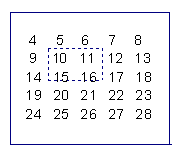14．如图：梯形纸片ABCD，∠B＝60°，AD∥BC，AB＝AD＝2，BC＝6．将纸片折叠，使点B与点D重合，折痕为AE，则CE＝　　　　  ．

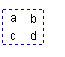15、如图是一个数表，现用一个矩形在数表中

任意框出4个数则

（1）a、c的关系是：__________________；

（2）当a＋b＋c＋d＝32时，a＝__________．

三、解答题（本大题有7题，其中第16、17题各6分；第18、19题各8分；第20、21、22题各9分，共55分）

16、计算:　

　

17、解方程：．

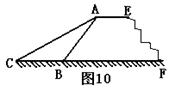
18．已知：如图（10），斜坡AB的长为100m，坡角是45°，现在需要添土把它改造成坡角为30°的斜坡AC，求原斜坡的底端B向前推进的距离BC（结果保留根号）.
 


19、为了解中学生的体能情况，某校随机抽取了部分学生进行一分钟跳绳次数测试．某同学将所得的数据进行整理，列出下表（未完成）：　

分组（跳绳次数x）

频数（学生人数）

频　率

60≤x<80

2

80≤x<100

0.1

100≤x<120

17

0.34

120≤x<140

0.3

140≤x<160

8

0.16

160≤x<180

3

n

合计

m

（1）求出上表中m，n的值；　

 

 

（2）一分钟跳绳次数小于100的学生人数占被测试学生总数的百分之几？

（3）这次测试中，学生跳绳次数的中位数落在哪个范围内？并说明理由．

20、某蔬菜商现要运送黄瓜30吨、大白菜13吨到深圳市内，计划租用甲、乙两种货车共10辆将这批货全部运到深圳市区，已知甲种货车可装黄瓜4吨和大白菜1吨，乙种货车可装黄瓜、大白菜各2吨；

（1）　　　 该菜商安排甲、乙两种货车时有几种方案？请你设计出来。

（2）若甲种货车每辆付运输费1000元，乙种货车每辆付运费800元，为使运费最少，则该菜商应选择哪种方案？最少运费是多少元？

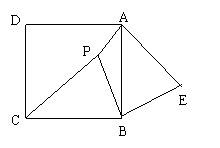
21、已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，

满足∠ABE=∠CBP，BE=BP；

（1）　　　 △CPB≌△AEB；

（2）　　　 求证：PB⊥BE；

（3）　　　 若PA ：PB=1 ：2，∠APB=135°，求cos∠PAE的值。


22、如图，已知直线与轴、轴分别交于Ａ、Ｂ两点，以ＯＡ为直径作半圆，圆心为Ｄ。Ｍ是ＯＢ上一动点（不运动到Ｏ点、Ｂ点），过Ｍ点作半圆的切线交直线于Ｎ，交ＡＢ于Ｆ，切点为Ｐ。连结ＤＮ交ＡＢ于Ｅ，连结ＤＭ。

（１）　 证明：∠ＯＭＤ＝∠ＡＤＮ；

（２）　 设ＯＭ，ＡＮ＝，求关于的函数解析式，并写出自变量的取值范围；

（３）　

x
 

y
 

M
 

B
 

F
 

P
 

D
 

A
 

N
 

E
 

O
 
当以Ａ、Ｆ、Ｎ为顶点的三角形与△ＡＤＥ相似时，求直线ＭＮ的解析式。