2005年初中毕业班质量检测试卷
数学科试题（满分：150分，考试时间：120分钟）
班级：__________姓名：__________座号：__________
一、填空题（每小题3分，共36分）
1、如果a的平方根是±2，则
＝__________。
2、一种细菌的半径是0.003728m，用科学计数法表示为____________________。
3、计算：
＝__________。
4、函数
的自变量x的取值范围是__________。
5、如果关于x的方程
的解为x＝－2，则a＝__________。
6、点P（－3，2）与点Q关于原点对称，则点Q在第__________象限。
7、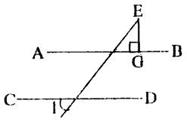
已知
，那么a：b＝__________。
8、如图，AB∥CD，EG⊥AB，垂足为G，若∠1＝50°，则∠E＝__________。
9、在△ABC中，∠C＝90°，BC＝2，SinaA＝
，则AB＝__________。
10、 用一张圆形的纸片剪一个边长为4cm的正六边形，则这个圆形纸片的半径最小应为__________cm。
11、
党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到年比年翻两番。在本世纪的头20年（2001——2020年），要实现这一目标，以十年为单位计算，设每个十年的国民生产总值的增长率为x，则列出方程为：______________________________。
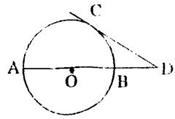
12、 已知：如图AB是⊙O的直径，BD＝OB，∠CAB＝30°，请根据已知条件和所给图形，写出三个正确结论。（除AO＝OB＝BD外）：①____________________；②____________________；③____________________。
二、选择题（每小题4分，共20分）
13、若分式
的值是零，则x的值是（ ）
A、－3 B、－1 C、3 D、±3
14、某同学使用计算器求30个数据的平均数时，错将其中的一个数据105输入为15，那么由此求出的平均数与实际平均数的差是（ ）
A、3.5 B、－3 C、0.5 D、3
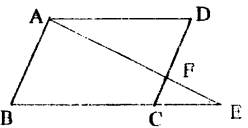15、如图，E是平行四边形ABCD的边BC的延长线上一点，连结AE交CD于F，则图中共有相似三角形的对数是（ ）
A、1 B、2 C、3 D、4
16、下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A、等边三角形 B、平行四边形 C、等腰三角形 D、圆
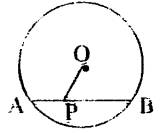17、如图，⊙O的直径为10cm，弦AB为8cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有（ ）
A、2 B、3 C、4 D、5
三、解答题（本大题共9小题，共94分）
18、（7分）解方程：
19、（8分）当x的倒数等于它本身时，求分式
的值。
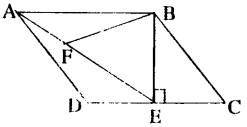
20、（9分）如图，在平行四边形ABCD中，过点B作BE⊥CD，连结AE，F为AE上一点，且∠BFE＝∠C
求证：（1）△ABF∽△EAD
（2）若AB＝4，∠BAE＝30°，求AE的长。
21、（10分）本题有两小题，只须任选一题进行解答，第（1）题8分，第（2）题10分，若全部解答，则以第（2）题计分。
（1）（8分）解方程：
（2）（10分）已知，
是关于x的方程
的两个正实数根，且满足
，求实数k的值。
22、（10分）
（1）计算下列各题
①
_______________
②
_______________
③
_______________
④
_______________
（2）仔细观察上面几道题及其计算结果，写出反映这种规律的一般结论：____________________________________________________________
用上述发现的规律直接写出下面的结果
＝______________________________
2004个 2004个
23、（10分）在某服装厂里有大量形状为等腰直角三角形的边角布料（如图）。现找出其中一种，测得∠C＝90°，AC＝BC＝4，今要从这种三角形中剪出一种扇形，做成不同形状的玩具，使扇形的边缘半径恰好都在△ABC的边上，且扇形的弧与△ABC的其它边相切，请设计出所有可能符合题意的方案示意图，并写出扇形的半径（只要求画出图形，并直接写出扇形的半径）
24、（12分）如图（1），AB是⊙O的直径，AP、AQ是⊙O的两条弦，过B点作⊙O的切线l，分别交AP、AQ于点M、N。
①证明：AP·AM＝AQ·AN
②将直线l向上平移，使其经过点P，如图（2），l交直线AQ于N，你能得出什么结论？试证明你的结论。
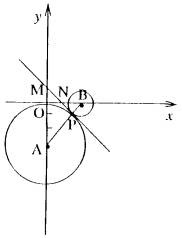
25、（14分）已知：如图，圆心A（0，－3），⊙A与x轴相切，⊙B的圆心B在x轴正半轴上，且⊙B与⊙A外切于点P，两圆的内公切线MP交y轴于点M，交x轴于点N
（1） 求证：△AOB∽△APM
（2） 设⊙A的半径为R1，⊙B的半径为R2，若R1：R 2＝3：2，求M、N的坐标及公切线MP的函数解析式。
（3） 设点B（X1，0），点B关于y轴的对称点B`（X2，0），若X1·X2＝－6，求过B`、A、B三点的抛物线解析式。
26、（14分）如图：已知矩形ABCD的面积为36，以此矩形的对称轴建立平面直角坐标系，设点A有坐标为（x，y），其中x＞0，y＞0。
（1） 求出y与x之间的函数关系式，求出自变量x的取值范围；
（2） 用x、y表示矩形ABCD的外接圆的面积S，并用下列方法，解答后面的问题：
方法：∵
（k为常数且k＞0，a≠0），
∴
∴当
，即
时，
取的最小值2k
问题：当点A在何位置时，矩形ABCD的外接圆面积S最小？并求出S的最小值。
（3） 如果直线
与x轴交于点P，与y轴交于点Q，那么是否存在这样的实数m，使得点P、Q与（2）中求出的点A构成△PAQ的面积是矩形ABCD的面积的
？若存在，请求出m的值；若不存在，请说明理由。
