初中几何综合测试题

（时间120分 满分100分）

一.填空题（本题共22分，每空2分）

1.一个三角形的两条边长分别为9和2，第三边长为奇数，则第三边长为 .
2.△ABC三边长分别为3、4、5，与其相似的△A′B′C′的最大边长是
　10，则△A′B′C′的面积是 .
4.弦AC，BD在圆内相交于E，且，∠BEC=130°，
　则∠ACD= .
5.点O是平行四边形ABCD对角线的交点，若平行四边行ABCD的面
　积为8cm，则△AOB的面积为 .
6.直角三角形两直角边的长分别为5cm和12cm，则斜边上的中线长为
　 　　　 .
7.梯形上底长为2，中位线长为5，则梯形的下底长为 .
　
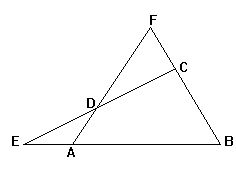
9.如图，分别延长四边形ABCD两组对边交于E、F，若DF=2DA，
　
　
10.在Rt△ABC中，AD是斜边BC上的高，如果BC=a，∠B=30°，
　那么AD等于 .
　

二．选择题（本题共44分，每小题4分）

　1.一个角的余角和它的补角互为补角，则这个角是 [ ]
　　A.30°　 B.45°　 C.60°　　 D.75°
　2.依次连结等腰梯形的各边中点所得的四边形是 [ ]
　　A.矩形　 B.正方形 C.菱形　　 D.梯形
　3.如图，DF∥EG∥BC,AD=DE=EB,△ABC被分成三部分的
　　面积之比为 [ ]
　　
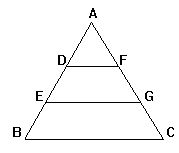
　　A.1∶2∶3　　　　 B.1∶1∶1
　　C.1∶4∶9　　　　 D.1∶3∶5
　4.如果两个圆的半径分别为4cm和5cm,圆心距为1cm，那么这两个圆
　　的位置关系是 [ ]
　　A.相交　　 B.内切　　 C.外切　　 D.外离
　5.已知扇形的圆心角为120°，半径为3cm,那么扇形的面积为[ ]
　　
　6.已知Rt△ABC的斜边为10，内切圆的半径为2，则两条直角边的
　　长为 [ ]
　　
　7.和距离为2cm的两条平行线都相切的圆的圆心的轨迹是 [ ]
　　A.和两条平行线都平行的一条直线。
　　B.在两条平行线之间且与两平行线都平行的一条直线。
　　C.和两平行线的距离都等于2cm的一条平行线。
　　D.和这两条平行线的距离都等于1cm的一条平行线。
　8.过圆外一点作圆的割线PBC交圆于点B、C，作圆的切线PM，M
　　为切点，若PB=2，BC=3，那么PM的长为 [ ]
　　
　9.已知：AB∥CD，EF∥CD,且∠ABC=20°，∠CFE=30°,
　　则∠BCF的度数是 [ ]
　　
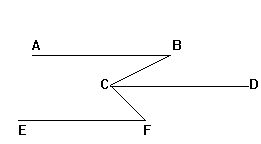
　　A.160° B.150° C.70° D.50°
　10.如图OA=OB，点C在OA上，点D在OB上，OC=OD，AD和
　　BC相交于E，图中全等三角形共有 [ ]
　　

　　A.2对　　 B.3对　　 C.4对　　　 D.5对
　11.既是轴对称，又是中心对称的图形是 [ ]
　　A.等腰三角形　　　　 B.等腰梯形
　　C.平行四边形　　　　 D.线段
　

三.计算题（本题共14分，每小题7分）
　　　

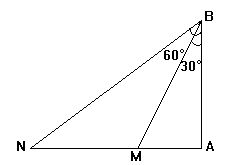
　第一次在B处望见该船在B的南偏西30°，半小时后，又望见该船
　在B的南偏西60°，求该船的速度．
　
2.已知⊙O的半径是2cm，PAB是⊙O的割线，PB=4cm,PA=3cm,PC
　是⊙O的切线，C是切点，CD⊥PO，垂足为D，求CD的长．
　
　

四．证明题（本题共20分，每小题4分）

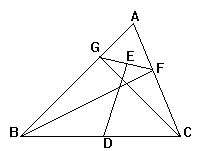
1.如图，在△ABC中，BF⊥AC,CG⊥AD,F、G是垂足，D、E分
　别是BC、FG的中点，求证：DE⊥FG
　
　
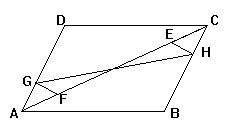
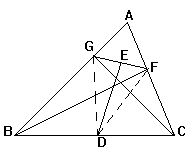
2.如图已知在平行四边形ABCD中，AF=CE，FG⊥AD于G，
　EH⊥BC于H，求证：GH与EF互相平分
　
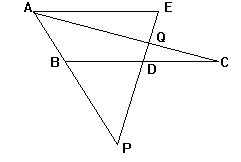
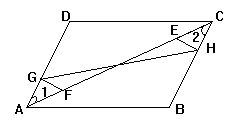
3.如图，AE∥BC,D是BC的中点，ED交AC于Q，ED的延长线交
　AB的延长线于P，求证：PD·QE=PE·QD
　
　
4.如图，在梯形ABCD中，AB∥DC，AD=BC，以AD为直径的圆
　O交AB于点E，圆O的切线EF交BC于点F.
　求证：（1）∠DEF=∠B;（2）EF⊥BC
　　
　
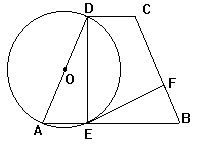
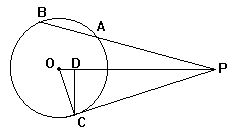
5.如图，⊙O中弦AC，BD交于F，过F点作EF∥AB，交DC延
　长线于E，过E点作⊙O切线EG，G为切点，求证：EF=EG
　

初中几何综合测试题参考答案
　 　

　　一. 填空（本题共22分，每空2分）
　　　 　1.9
　　 　　2.24
　　　　 　
　　 　　　
　 　　　　
　 　　　　
　
　　二. 选择题（本题共44分，每小题4分）
　　　　　1.B 　　2.C　　　 3.C　　　 4.B　　　　 5.A
　　　　　6.C　　 7.D　　　 8.C　　　 9.D　　　　10.C
　　　　 11.D
　
　　三.（本题共14分，每小题7分）
　　　　解1：
　　　　　　　
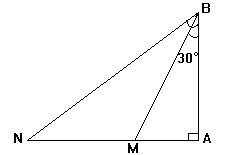
　　　　如图：∠ABM=30°，∠ABN=60° ∠A=90°，AB=
　　　　　　　
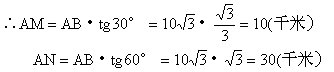
　　　　　　∴MN=20（千米），即轮船半小时航20千米，
　　　　　　∴轮船的速度为40千米/时
　　　　　
　
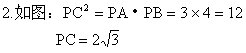
　　　　　　∵PC是⊙O的切线
　　　　　　　
　　　　　又∵CD⊥OP
　　　　　　∴Rt△OCD∽Rt△OPC
　　　　　　　
　　　　　　　
　
　
　　四.证明题（本题共20分，每小题4分）
　　　　1.证明：
　　　　　　　
　　　　　　　连GD、FD
　　　　　　　∵CG⊥AB,BF⊥AC,D是BC中点
　　　　　　　　
　　　　　　　∴GD=FD, △GDF是等腰三角形
　　　　　　又∵E是GF的中点
　　　　　　　∴DE⊥GF
　
　　　　2.证明：
　　　　　　　
　　　　　　　∵四边形ABCD是平行四边形
　　　　　　　∴AD∥BC
　　　　　　　　∠1=∠2
　　　　　　　又AF=CE
　　　　　　　　∠AGF=∠CHE=Rt∠
　　　　　　　Rt△AGF≌Rt△CHE
　　　　　　　∴EH=FG,又FG⊥AD，EH⊥BC，AD∥BC
　　　　　　　∴FG∥EH
　　　　　　　∴四边形FHEG是平行四边形，
　　　　　　而GH，EF是该平行四边形的对角线
　　　　　　　∴GH与EF互相平分
　
　　　　3.证明：
　　　　　　　
　　　　　　∵AE∥BC
　　　　　　∴∠1=∠C, ∠2=∠3
　　　　　　∴△AQE∽△CQD
　　　　　　　　
　　　　　又∵AE∥BC
　　　　　　　　
　　　　　又∵BD=CD
　　　　　　∴
　　　　　即PD·QE=PE·QD
　
　　　4.证明：
　　　　　　
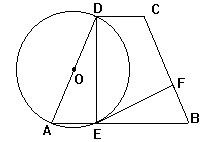
　　　(1)在梯形ABCD中，DC∥AB，AD=BC
　　　　　∴∠A=∠B
　　　　　∵EF是⊙O的切线
　　　　　∴∠DEF=∠A
　　　　　∴∠DEF=∠B
　　　(2)∵AD是⊙O的直径
　　　　　∴∠AED=90°，∠DEB=90°
　　　　即∠DEF+∠BEF=90°
　　　　又∵∠DEF=∠B
　　　　　∴∠B+∠BEF=90°
　　　　　∴∠EFB=90°
　　　　　∴EF⊥BC
　　　5.证明：
　　　　　　
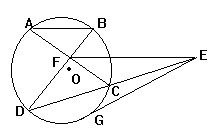
　　　　　∵EF∥AB
　　　　　∴∠EFC=∠A
　　　　　∵∠D=∠A
　　　　　∴∠EFC=∠D
　　　　又∠FEC=∠DEF
　　　　　∴△EFC∽△EDF
　　　　　　　
　　　　即EF=EC·ED
　　　　又∵EG切⊙O于G
　　　　　∴EG=EC·ED
　　　　　∴EF=EG
　　　　　∴EF=EG