2005~2006学年度第二学期

初三数学试卷

题号	一	二	三	四				五			合计
				16	17	18	19	20	21	22
得分

　　　

　　　　说明：1.考试时间为90分钟，满分为120分。

2.考试内容：代数至13章　几何至7章

　　　

 一、选择题（每小题3分，共15分）

　1、如果反比例常数的图象经过点P（－2，3），则k的值（　　　）

A．—6　　 B．—　　C．—　　  D．6

　　　　2、半径分别为1cm和5cm的两圆相交，则圆心距d的取值范围是（　　 ）

　　　　  A．d<6　　 B. 4<d<6　　C. 4≤d<6　　 D. 1<d<5

3、如果圆柱的底面半径为4㎝，母线长为5㎝，那么它的侧面积（　　　）

A．20π　B．40π　C．20　D．40

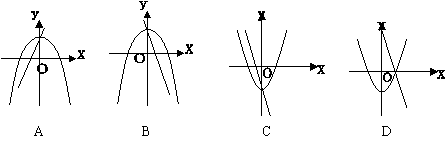
　　　　4、在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax²+c的图像大致为（　）

　　　　

　　　

　　　　5、已知：如图，在⊙O中，AB是直径，四边形ABCD内接于⊙O，∠BCD=130°，

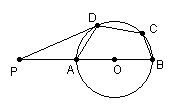过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　 ）

　　　　  A．45°　　B.40°　　C.50°　　 D.65°

　　　　

　　　 二、填空题（每小题4分，共20分）

　　　　 6、已知：2+是关于x的方程x² - 4x + c=0的一个根，

　　 则c的值为____________。

 7、若正六边形的半径为4cm，则它的边长为________，面积为________。

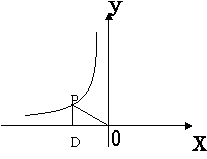8、如图，点P是反比例函数y=上的一点，PD⊥x轴于点D，

则△POD的面积为______________。

9、已知反比例函数y=与一次函数y=2x+k的图像　

的一个交点的纵坐标是—4，则k的值为_______。

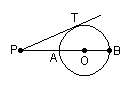10、已知如图PT切⊙O于点T，经过圆心的割线PAB

交⊙O于点A和B，PT=4PA＝2，则⊙O的半径是____________

三、解答下列各题（每小题6分，共30分）

11、先化简再求值其中x＝

12、解方程：

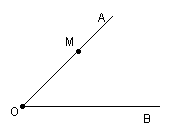13、已知∠AOB的边OA上有一点M，

作一弧将∠AOB的两边连接起来，

且使弧与OA在M处连接。

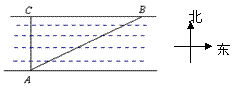
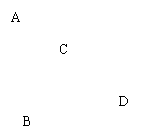
14、如图,为了测量一条河的宽度,一测量员在河岸边的C处测得对岸一棵树A在正南方向,测量员向正东方向走180米到点B处,测得这棵树在南偏西60°的方向,求河的宽度（结果保留根号）.

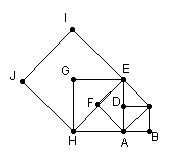15、设四边形ABCD是边长为1的正方形，以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以第二个正方形的对角线AE为边作第三个正方形AEGH，如此下去···。

（1）记正方形ABCD的边长为＝1，依上述方法所

作的正方形的边长依次为，，，···，，

求出，，的值。

（2）根据以上规律写出第n个正方形的边长的表达式。

四、解答题（每小题7分，共28分）

 16、已知关于x的一元二次方程x² + (2m-3)x + m² = 0的两个不相等的实数根

α、β满足=1，求m的值。

17、如图，已知两直线和，求它们与y轴所围成的三

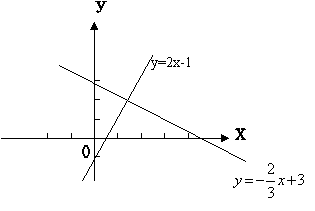角形的面积。

 18、李明与王云分别从A、B两地相向而行，若两人同时出发，则经过80分钟

两人相遇；若李明出发60分钟后王云再出发，则经过40分钟两人相遇，问李明

与王云单独走完AB全程各需多少小时？

19、已知：AB为⊙O的直径，P为AB延长线上的一点，过点P作⊙O的切线，切

点为C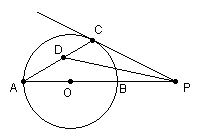，∠APC的平分线交AC于点D，求∠CDP的度数。

五、解答题（每小题9分，共27分）

20、已知：抛物线

1）　用配方法求它的顶点坐标和对称轴；

2）　若该抛物线与x轴的两个交点为A、B，求线段AB的长。

21、今年以来，广东大部分地区的电力紧缺，电力公司为鼓励市民节约用电，采取按月用电量分段收费办法，若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：

（1）分别写出当0≤x≤100和x≥100时，y与x的函数关系式；

（2）利用函数关系式，说明电力公司采取的收费标准；

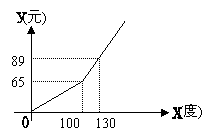（3）若该用户某月用电62度，则应缴费多少元？若该用户某月缴费105元时，则该用户该月用了多少度电？

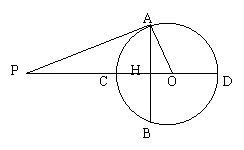
22、已知：在⊙O中，AB是弦，CD是直径，AB⊥CD，H是垂足，点P在DC

的延长线上，且∠PAH=∠POA，OH∶HC=1∶2，PC=6，

1）求证：PA是⊙O的切线

　2）求⊙O的半径的长

　3）试在弧AB上任取一点E（不与点A、B重合）连结PE并延长与弧ADB交于

点F，设 EH=x ，PF=y ，求x与y的函数关系式，并求出自变量x的取值范围。

答案：

一、ABBBB

二、6、1　 7、4cm　24cm²　 8、1　 9、-8　　10、15/4

三、11、原式=　　4-2

12、x₁=0　x₂=－3/2　 13、略　　14、60 米

15、

16、m=－3　　

17、C（3/2，2）A(0，3) B(0，－1)　AB=4　S_△ABC=1/2 ×4×3/2=3

18 解：设李明需x小时，王云需y小时。

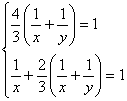　 解得：x=2　y=4

19、提示：连结BC ∠CDP=45°

20、1)顶点坐标（－1，－3）　对称轴x=－1

　　2)AB=2

22、1）略

　　　　2) ∵OH∶HC=1∶2　 ∴设OH=x则HC=2x　OA=3x

　　　　 ∵∠OAP=90° AB⊥CD

　　　　 ∴　∴AO²=PO·OH　

 ∴9x²=(6+3x)·x　∴x₁=1 x₂=0(不合题意，舍去)

∴OA=3x=3　 ∴⊙O的半径为3

3）∵∠OAP=90° AB⊥CD

　 ∴　 ∴PA²=PO·PH

　∵PA是切线，PEF是割线

　∴PA²=PE·PF　 ∴PO·PH=PE·PF

　∴ 　∵∠HPE=∠FPO ∴△HPE∽△FPO

 ∴　∴　∴y=

∵OA=3　OH=1　∴AH==2　∴2≤x<2

x与y的函数关系式为：y=（2≤x<2）