威海市2006年初中升学考试
数 学
(时间120分钟,满分120分)
请同学们注意:
1.答卷前请将密封线内的项目填写清楚。
2.本试卷分为第I卷和第II卷两部分,共10页。第I卷(1至2页)为选择题,第II卷(3至10页)为非选择题。第I卷(选择题)的答案须填写在第3页的答案表中,第II卷(非选择题)用蓝、黑色钢笔或圆珠笔直接答在试卷上。考试结束时,将试卷全部上交。
3.凡要求保留精确度的题目,要用计算器计算,计算过程中的数据不要四舍五入;不要求保留精确度的题目,计算结果保留准确值。
第I卷 (选择题,共36分)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个是正确的.每小题选对得3分,选错、不选或多选,均不得分)
1.据威海新闻网报道,今年“五一”黄金周约有110万游客饱览我市美景,游客在威海游玩期间人均消费840元,我市“五一”黄金周的旅游收入用科学计数法表示为(保留三个有效数字) ( )
(A)9.24×107 (B)9.24×108 (C)0.924×109 (D)9.24×109
2.下列图形中,既是轴对称图形又是中心对称图形的是 ( )
(A)平行四边形 (B)正八边形 (C)等腰梯形 (D)等边三角形
3.![]() 的绝对值等于
( )
的绝对值等于
( )
 (A)
(A) ![]() (B)-
(B)-![]() (C)
(C)![]() (D)-
(D)-![]()
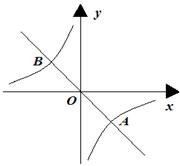
4.如图,过原点的一条直线与反比例函数![]() (k≠0)的图像分别交于A、B两点.若A点的坐标为(a,b),则B点的坐标为
(
)
(k≠0)的图像分别交于A、B两点.若A点的坐标为(a,b),则B点的坐标为
(
)
(A)(a,b)
(B)(b,a)
(C)(-b,-a)
(D)(-a,-b)
![]() 5.如图,数轴上所标出的点中,相邻两点间的距离相等,则点A表示的数为
( )
5.如图,数轴上所标出的点中,相邻两点间的距离相等,则点A表示的数为
( )
(A)30 (B)50 (C)60 (D)80
 6.如图,在△ABC中,∠ACB=100º,AC=AE,BC=BD,则∠DCE的度数为
( )
6.如图,在△ABC中,∠ACB=100º,AC=AE,BC=BD,则∠DCE的度数为
( )
(A)20º
(B)25º
(C)30º
(D)40º
7.用换元法解方程![]() 时,设
时,设![]() ,则原方程可变形为 ( )
,则原方程可变形为 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
8.用半径为30cm,圆心角为120º的扇形围成一个圆锥的侧面,则圆锥的底面半径为( )
(A)10 cm (B)30 cm (C)45 cm (D)300 cm
9.标价为x元的某件商品,按标价八折出售仍能盈利b元,已知该件商品的进价为a元,则x等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
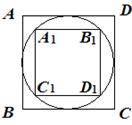
10.如图,若正方形A1B1C1D1内接于正方形ABCD的内接圆,则![]() 的值为( )
的值为( )
 (A)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.已知a、b为一元二次方程![]() 的两个根,那么
的两个根,那么![]() 的值为( )
的值为( )
(A)-7 (B)0 (C)7 (D)11
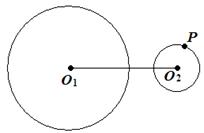
12.如图,⊙O1的半径为1,O1O2=6,P为⊙O2上一动点,过P点作⊙O1的切线,则切线长最短为 ( )
(A)![]() (B)5
(C)3
(D)
(B)5
(C)3
(D)![]()
 |
绝密★启用前 试卷类型:A
威海市2006年初中升学考试
数 学
第I卷 选择题答案表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 | 评卷人 |
| 答案 |
第II卷 (非选择题,共84分)
| 得分 | 评卷人 |
二、填空题(本大题共6小题,每小题3分,共18分.只要求填出最后结果)
13.写出一个-6~-5之间的无理数: .
14.计算![]() = .
= .
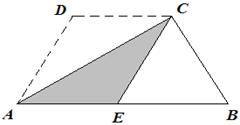
15.如图,梯形纸片ABCD,已知AB∥CD,AD=BC,AB=6,CD=3.将该梯形纸片沿对角线AC折叠,点D恰与AB边上的E点重合,则∠B= .
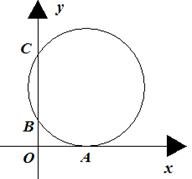 |
16.如图,一圆与平面直角坐标系中的x轴切于点A(8,0),与y轴交于点B(0,4),C(0,16),则该圆的直径为 .
17.将多项式![]() 加上一个整式,使它成为完全平方式,试写出满足上述条件的三个整式:
加上一个整式,使它成为完全平方式,试写出满足上述条件的三个整式:
, , .
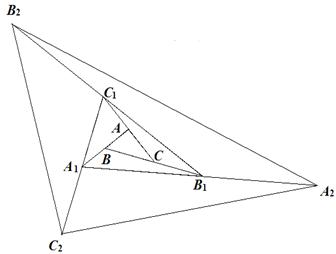
18.如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=
AB,B1C= BC,C1A=CA,顺次连结A1,B1,C1,得到△A1B1C1. 第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1= A1B1,B2C1= B1C1,C2A1= C1A1,顺次连结A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2006,最少经过 次操作.
三、解答题(本大题共7小题,共66分)
| 得分 | 评卷人 |
19.(7分)
先化简,再求值:
![]() ,其中a =
,其中a =![]()
| 得分 | 评卷人 |
20.(7分)
某学校举行实践操作技能大赛,所有参赛选手的成绩统计如下表所示(满分10分)
| 分数 | 7.1 | 7.4 | 7.7 | 7.9 | 8.4 | 8.8 | 9 | 9.2 | 9.4 | 9.6 |
| 人数 |
(1)本次参赛学生成绩的众数是多少?
(2)本次参赛学生的平均成绩是多少?
(3)肖刚同学的比赛成绩是8.8分,能不能说肖刚同学的比赛成绩处于参赛选手的中游偏上水平?试说明理由.
| 得分 | 评卷人 |
21.(8分)
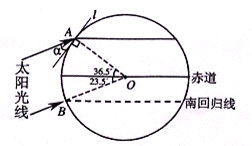
图①,②是晓东同学在进行“居民楼高度、楼间距对住户采光影响问题”的研究时画的两个示意图.请你阅读相关文字,解答下面的问题.
(1)图①是太阳光线与地面所成角度的示意图.冬至日正午时刻,太阳光线直射在南回归线(南纬23.5º)B地上.在地处北纬36.5º的A地,太阳光线与地面水平线l所成的角为![]() ,试借助图①,求
,试借助图①,求![]() 的度数.
的度数.
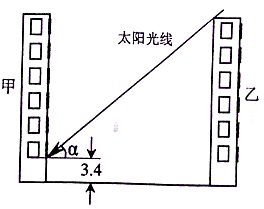 (2)图②是乙楼高度、楼间距对甲楼采光影响的示意图.甲楼地处A地,其二层住户的南面窗户下沿距地面3.4米.现要在甲楼正南面建一幢高度为22.3米的乙楼,为不影响甲楼二层住户(一层为车库)的采光,两楼之间的距离至少应为多少米?
(2)图②是乙楼高度、楼间距对甲楼采光影响的示意图.甲楼地处A地,其二层住户的南面窗户下沿距地面3.4米.现要在甲楼正南面建一幢高度为22.3米的乙楼,为不影响甲楼二层住户(一层为车库)的采光,两楼之间的距离至少应为多少米?
 |
图① 图②
| 得分 | 评卷人 |
22.(10分)
小明和小亮共下了10盘围棋,小明胜一盘计1分,小亮胜一盘计3分.当他俩下完第9盘后,小明的得分高于小亮;等下完第10盘后,小亮的得分高于小明.他们各胜过几盘?(已知比赛中没有出现平局)
| 得分 | 评卷人 |
23.(10分)
已知:如图①,在□ABCD中,O为对角线BD的中点.过O的直线MN交直线AB于点M,交直线CD于点N;过O的另一条直线PQ交直线AD于点P,交直线BC于点Q,连结PN、MQ.
(1)试证明△PON与△QOM全等;
(2)若点O为直线BD上任意一点,其他条件不变,则△PON与△QOM又有怎样的关系?试就点O在图②所示的位置,画出图形,证明你的猜想;
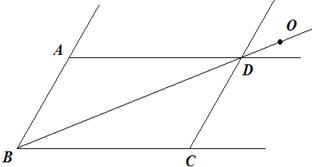
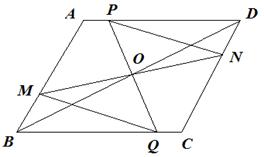 (3)若点O为直线BD上任意一点(不与点B、D重合),设OD:OB=k,PN=x,MQ=y,则y与x之间的函数关系式为 .
(3)若点O为直线BD上任意一点(不与点B、D重合),设OD:OB=k,PN=x,MQ=y,则y与x之间的函数关系式为 .
图① 图②
| 得分 | 评卷人 |
24.(12分)
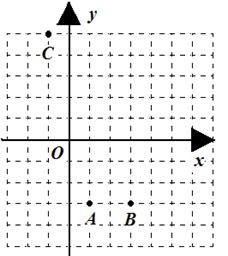
抛物线y = ax2+bx+c (a≠0)过点A(1,-3),B(3,-3),C(-1,5),顶点为M点.
(1)求该抛物线的解析式.
(2)试判断抛物线上是否存在一点P,使∠POM=90º.若不存在,说明理由;若存在,求出P点的坐标.
(3)试判断抛物线上是否存在一点K,使∠PMK=90º,说明理由.
 |
| 得分 | 评卷人 |
25.(12分)
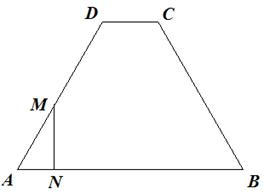
在梯形ABCD中,AB∥CD,AB=8cm,CD=2cm,AD=BC=6cm,M、N为同时从A点出发的两个动点,点M沿A→D→C→B的方向运动,速度为2cm/秒;点N沿A→B的方向运动,速度为1cm/秒.当M、N其中一点到达B点时,点M、N运动停止.设点M、N的运动时间为x秒,以点A、M、N为顶点的三角形的面积为y cm2.
(1)试求出当0 < x < 3时,y与x之间的函数关系式;
(2)试求出当4 < x < 7时,y与x之间的函数关系式;
(3)当3 < x < 4时,以A、M、N为顶点的三角形与以B、M、N为顶点的三角形是否有可能相似?若相似,试求出x的值. 若不相似,试说明理由.
 |
 |
 |