《二次函数》测试卷

（满分150分；完卷时间100分钟）

班级　　　　  姓名　　　　　　　  成绩　　　　　　 

一．选择题（每题3分，共30分）

1．　下列各式中，y是的二次函数的是　 　　　　　　　　　　　　　　　　( 　　)

A．　　　B．　　　C．　　　D．

2．在同一坐标系中，作+2、-1、的图象，则它们　( 　　)

A．都是关于轴对称　　　B．顶点都在原点　 C．都是抛物线开口向上　　　　 D．以上都不对

3．下列对二次函数、、为常数）叙述不正确的是（　　）

A　 二次函数因变量一定有最大值或最小值　　　  B　二次函数图像是轴对称图形

C　 二次函数图象一定会与轴相交　　　　　　  D　二次函数图像一定过原点

4．若二次函数的图象经过原点，则的值必为　 　　 ( 　　)

A．　 0或2 　　　B．　 0　 　　　 C．　　2 　　　　 D．　　无法确定

5．已知原点是抛物线的最高点，则的范围是　 　　　　　　　 ( 　　)

A．　　　　B．　　　　 C．　 　　 D．　

6．关于没有实数根，则的图象的顶点在　　　　  （　　 ）

A　 第一象限　　　　　 B　　第二象限　 C　 第三象限　　　　  D　　第四象限　　

7．在同一直角坐标系中，函数与的图象大致如图 （　　）

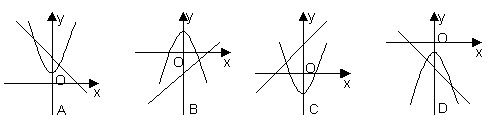8．抛物线则图象与轴交点为　　　　　　　　　　　　 （　　）

A．　 二个交点　 　B．　一个交点　　　C．　　 无交点　 　　 D．　　不能确定

9．不经过第三象限，那么的图象大致为  （　　）

y　　　　　　　　 y　　　　　　　　　　  y　　　　　　　 y

O　　　x　　　  O　　　　 x　　　　　 O　　 x　　　　　 O　　　 x

　　　A　　　　　　　　 B　　　　　　　　　 C　　　　　　　　　 D

10．对于的图象下列叙述正确的是　　 　　　　　　（　　）

A　 顶点作标为(－3，2)　　　　　　　  B　　对称轴为y=3

C　 当时随增大而增大　　　  D　　当时随增大而减小

二．填空题：（每题3分，共15分）

11．当时，函数是二次函数；

12． 写出一个开口向上，顶点坐标是（2，-3）的函数解析式 　　　　　　　　　　 ；

13．函数、、为常数）的对称轴是　　　　  ；顶点坐标是　　　　 ；

14．抛物线的图象向右移动两个单位，再向下移动一个单位，它的顶点坐标是　　　　  ，对称轴是　　　　　 解析式是　　　　　　  ；

15．如果抛物线和直线都经过点P(2，6)，则_______，=_______，抛物线不经过第_______象限．

三．解答题(共105分)

16．（8分）若抛物线经过点A（，0）和点B（-2，），求点A、B的坐标。

17．（7分）请设计一个开口向下，与轴交于（-1，0）、（3，0）的二次函数解析式，并指出它的对称轴。

18．（8分）已知抛物线的顶点在轴上，求这个函数的解析式及其顶点坐标。

19．（8分）若二次函数的图象与直线没有交点，求的取值范围。

20．（12分）已知二次函数的图象的顶点坐标为（3，-2）且与轴交与（0，）

（1）求函数的解析式，并画于它的图象；

（2）当为何值时，随增大而增大。

21．（10分）若直线与二次函数的图象与交A、B两点，求以A、B及原点O为顶点的三角形的面积。

22．（6分）一台机器原价为60万元，如果每年的折旧率为，两年后这台机器的价格为万元，求与函数关系式，若折旧率以10%计算，那么两年后的该机器价值为多少？

23．（12分）某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，若每千克涨价一元，日销售量将减少20千克。

（1）现要保证每天盈利6000元，同时又要让顾客得到实惠，那么每千克应涨价多少元？

（2）若该商场单纯从经济角度看，那么每千克应涨价多少元，能使商场获利最多。

24．（16分）某市人民广场上要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流（在各个方向上）沿形状相同的抛物线路径落下（如图所示）。若已知OP＝3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米。

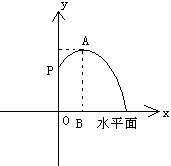（1）求这条抛物线的解析式；

（2）若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外。

25．（18分）二次函数的图象与x轴从左到右两个交点依次为A、B，与y轴交于点C，

（1）求A、B、C三点的坐标；

（2）如果P(x，y)是抛物线AC之间的动点，O为坐标原点，试求△POA的面积S与x之间的函数关系式，并写出自变量x的取值范围；

（3）是否存在这样的点P，使得PO=PA，若存在，求出点P的坐标；若不存在，说明理由。