初三上期末综合基础复习题（1）

（一元二次方程、三角形函数、圆相关知识）

一、选择题

1．下列方程是一元二次方程的有（　　）

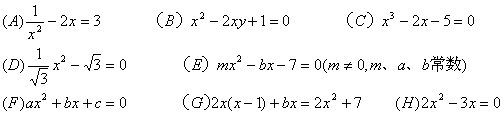
2．是关于x的一元二次方程，则（　　）

（A）p= 1　　(B)p>0　　 (C)p≠0　　(D)p为任意数

3，方程的常数项是（　　）

　（A）5　　　（B）3　　　　（C）－3　　（D）0

4．如图，在Rt△ABC中，∠C＝90°，

BC＝5，AC＝12，则cos∠B＝（　　）

5．若锐角a大于30°，则cot∠a的值一定是（　　　）

6．已知：锐角△ABC中，各边长都扩大为原来的m倍，则锐角∠A的各三角函数值（　　　）

（A）都扩大到m倍　　　(B)都扩大到(m＋1)倍

（C）不变　　　　　　　 (D)不能确定

7、已知⊙O的直径是10，P点到圆心O的距离为8，则P点与⊙O的位置关系是（　　）

  A、在圆外　 B、在圆心　 C、在圆上　 D、无法确定

8、△ABC的外心是三角形的（　 ）

　A、三条高的交点　　　　  B、三边中线的交点

　C、三条角平分线的交点　　D、三条边垂直平分线的交点

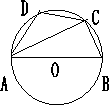
 9、如图：若AB是圆的直径，∠BAC=40°，则∠D=（　　）

  A、150°　 B、130°　　C、100°　　D、90°

初三上期末综合基础复习题（2）

（一元二次方程、三角形函数、圆相关知识）

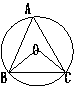
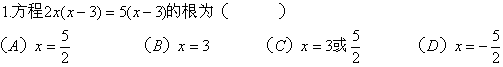
2、如图，在⊙O中，∠OBC=35°，则∠A=（　　）

  A、25°　B、50°　C、65°　D、55°

3.方程的根是（　　）

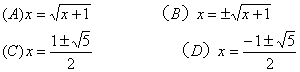
4．方程（x＋1）（x－1）＋2＝0的解是（　　）

（C）没有实数解　　　　　　　（D）无法确定

5、如图：在⊙O中，AB=8，圆心O到AB的距离为3，则⊙O的半径是（　　）

　A、5　　B、6　　C、8　　　 D、10

6．若锐角∠a满足cot∠a·cot23°=1，则∠a为（　　）

（A）27°　　（B）67°　　（C）23°　　（D）77°

7.将改写成下列式子，其中错误的是(　 )

(A)sin30°sinB+cos30°cosB　　 (B)cos60°sinB+sin60°cosB

(C)sin30°sinB+sin60°cosB　　 (D)cos60°sinB+sin30°cosB

8.在Rt△ABC中，∠C＝90°，如果，则cot∠B为(　)

9、已知，如图：PA=2，AB=6，PC=3，则PD=（　　）

A、　　B、4　　C、7　　　 D、

初三上期末综合基础复习题（3）

（一元二次方程、三角形函数、圆相关知识）

1．方程用配方法解时，应先化为（　　　）

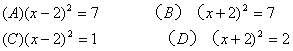
2．下列方程中有两个相等的实根的是（　　）

3．若a、c异号，则方程a）(a≠0)的根的情况是（　　）

（A）有两个相等的实数根　　　（B）有两个不相等的实数根

（Ｃ）没有实数根　　　　　（Ｄ）不能确定有无实数根

4、如图：四边形ABCD内接于圆，AD∥BC，则与∠CAD相等的角有（　　）个

 A、4　　　 B、3　　　　C、2　　　　 D、1

5.若，则锐角A一定（　　　）

（A）　　　 小于60°（B）大于60°（C）小于30°（D）大于30°

6.在Rt△ABC中，∠A＝90°，AD⊥BC，垂足为点D，若BC＝m，∠B＝a，则AD长为(　　 )

7.等边三角形的高为 ，则它的面积为(　　)

8、在⊙O中，∠AOB=100°，则∠ACB=（　　）

 A、100°　　B、120°　　C、130°　　D、140°

9、下列命题中真命题是（　 ）

 A、相等的圆周角所对的弧相等　　　 B、相等的圆周角所对的弧相等

C、90°的圆周角所对的弦是直径　　 D、相等的圆心角所对的弧是等弧

初三上期末综合基础复习题（4）

（一元二次方程、三角形函数、圆相关知识）

１.已知关于x的方程有两个实数根，则m的取值范围为（　　　）

***如改为有实数根，则求m的取值范围（　　　　　）

2.对任意实数m，关于x的方程一定（　　）

（A）有两个相等的实数根　　　（B）有两个不相等的实数根

（Ｃ）有两个实数根　　　　　　（Ｄ）没有实数根　　

3.已知：5与－9为方程的两个根，则（　　）

（A）p＝－4、q＝－45　　 (B) p＝－45、q＝－4

（C） p＝4、q＝－45　　　（D） p＝－45、q＝4

4.在Rt△ABC中，∠C＝90°，∠B＝30°，且b＋c＝12，则△ABC的周长为(　　)

5．在Rt△ABC中，∠C＝90°，，a=2，则b＋c＝（　　）

（A）　9　　　　（B）　8　　　（C）4　　　（D）6

_{6．在Rt△ABC中，∠C＝90°，则cosA·cotB的值为（　 ）}

7、如图：PE切⊙O于E，AB=7，DP=8，

AD：BC=1：2，则PE=（　　）

 A、7　　B、8　　 C、10　　　 D、12

8．圆内接四边形的顶点分圆周为1：3：2：4，则四边形各内角的度数为（　　　）

（A）　　　72°、144°、108°、36°（B）108°、90°、72°、90°

（C）126°、108°、54°、72°（D）126°、90°、54°、90°

9．已知：圆的直径为14cm，且圆心以到直线AB的距离为8cm，则直线与圆的位置关系（　　）

（A）相交　　（B）相切　　（C）相离　　（D）无法确定

10.若关于x的方程ax²+2x+1=0有两个不相等的实数根，则a的取值范围是（　　）

 A.a≠0且a﹤1　 B.a﹥1　　C.a=1　　D.a﹤1

二．填空题：

1.　　 计算

2.　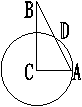　 当a＝＿＿＿＿（a为锐角）时，无意义。

3计算

4、如图：在△ABC中，∠C=90°，∠B=25°，

C为圆心，CA为半径，则AD=______度

5、已知，直角三角形的两条边分别为5cm 和12cm ，则它的内切圆半径为_______，外接圆半径是________。

6、一条弦把圆分成的度数之比为1：5的两条弧，若圆的半径为R，则弦心距为__________ (用R的代数式表示)

二、设x₁,x₂是关于x的方程：x²+(2m+1)x+(m-2)²=0的两个实数根，且,求m的值。

三、开发公司生产的960件新产品，需要精加工后，才能投放市场。现有甲、乙两个工厂都想加工这批产品，已知甲工厂单独加工完成这批产品比乙工厂单独加工完这批产品多用20天，而乙工厂每天比甲工厂多加工8件产品。公司需付甲工厂加工费用每天80元，乙工厂加工费用每天120元。

1求甲、乙两个工厂每天各能加工多少件新产品？

2．公司制定加工方案如下：可以由每个厂家单独完成；也可以由两个厂家同时合作完成。在加工过程中，公司只派一名高级工程师每天进行技术指导，（如两家同时生产也是用同一个工程师进行指导）并负担每天5元的误餐补助费。

请你帮助公司选择一种既省时又省钱的加工方案，并说明理由。

二、填空题　

1．　Rt△ABC中，∠C＝90º，若

2．　计算

3．

4、如图：AB是⊙O的切线，AD=12，AC：CD=1：5，则AB= ________

5、已知直径AB和弦CD相交于点E，若_________________________，则CE=DE（只需填一个适当的条件）

6．已知一个弓形的桥跨度为24米，弓高为5米，则弓形所在圆的半径为＿＿＿＿＿

7.以-2和3为根的一元二次方程是（　　）

8.若分式的值为0，则x的值为（　　）

9．分式方程的解为（　　）

三、已知：如图在Rt△ABC中，∠C＝90º，

，∠BDC＝45º，DC＝6，求AB长？

四、

2、如图二：水坝的横截面为梯形ABCD，坝宽AD=6米，

坡面CD=8米，AB的坡度为1：3，∠ADC=135º，

求：BC与AB的长？　　　　　　　　　　　　　A　　 　　D

B　　　　　  　　　　　　　　 　 C

二、填空题

1．已知CD是Rt△ABC斜边AB边上的高为12，，则AB＝＿＿＿＿

2．直角三角形中，一锐角的正切值为，周长为60cm，则三边长分别为＿＿＿＿＿

3．一个梯形它的两个下底分别为30º和45º，

较大的腰长为10m。则它的两底差为＿＿＿

4．已知AB是⊙O的直径，DE是⊙O的切线，

∠ACD=120°，则∠A= _____，∠ACE＝＿＿＿

5．若方程是一元二次方程，则m＝＿＿＿＿＿

6.方程(x+3)²=2的解是__________________

7.设x₁、x₂是方程2x²＋5x－1=0的两个根，则=________

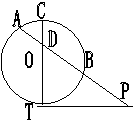
8、已知CT是⊙O的直径，PT是⊙O的切线，

CD=2，AD=3，BD=6，则PB=____________

三、已知：如图，在△ABC中，AB=4，BC=3，∠B=90°，点D在AB上运动，且D点不与A、B两点重合，过B、C、D三点作圆交AC于E点，连结ED。（1）设AD=x，CE=y，求y关于x的函数关系式，并指出自变量x的取值范围；（2）当AD之长是关于x的方程x²-mx+9=0的整数根时，求m的值及相应的四边形BCDE的面积。

　 C

　　　　　　　　　　　　　

　 B　　　　　　　　　　　　　 A

四．证明不论m为何值时，关于x的方程2x²＋3(m－1)x＋m²－4m－7=0有两个不相等的实数根

二、填空题

1．在△ABC中，∠C＝90º，，则斜边c＝＿＿＿＿

2．沿坡面前进50m则上升5m，则坡面的坡比为＿＿＿＿

3．计算

4．在坡比为1：2的AB上植树，两树间的水平距离为4米，

则两相邻树间的坡面距离为＿＿＿＿

5．关于x的一元二次方程(m-1)x²+2mx+m+3=0有两个不相等的实数根，则m的取值范围是__________________

6、以方程3x²＋x－1=0的两根之和与两根之积为根的一元二次方程是（　　）

7.在实数范围内分解因式：2x²＋5x－1=____________________________

三、知：如图，⊙O₁和⊙O₂相交于A、B，AC是⊙O的直径，CA、CB与⊙O₂相交于D、E，AC=12，CE=36，AD=BC，求（1）BC的长；（2）⊙O₂的半径；（3）sin∠BDE的值。

　　　　　 

　　　　

　　

C　　　　　　　　　  E　　E

四、在数学活动课上，老师带领学生测河宽，某学生在A处测到河对岸水边有一点C，并且测得∠CAD=45º，在距离A点50米的B处测得

∠CBD=30º，求：河宽CD长　 　　　　　　　C

　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　  D　　　 A　　 B

初三上期末综合基础复习题（5）

（一元二次方程、三角形函数、圆相关知识）

1、x₁,x₂是的两个根，则的值是（　　）

  A、3　　　　B、-3　　　 C、　　　　 D、

2、关于x的方程的一个根是2，设方程一个根为x₁，则有（　　）

  A、x₁=，k=-7　　　　　  B、x₁=，k=-7

  C、x₁=，k=7　　　　　  D、x₁=，k=7

3、以的两根之和与积为两个根的一元二次方程是（　　）

　A、　　　　　  B、

  C、　　　　　  D、

4.斜面坡度I＝1：3，则坡角∠a满足（　　）

　

5．沿坡角为30º的斜面前进100米，则上升的高度为（　　）

　

6．菱形ABCD的两条对角线AB＝6，BD＝4，则的值为（　　）

7、如图：若AB、AC是⊙O的切线，

∠A=40°，则∠D=（　　）

 A、140°　　 B、40°　

C、70°　　　 D、50°

8．已知△ABC的内心O，且∠A＝50°，则∠BOC＝（　　　）

　A、100°　　　B、130°　　C、65°　　D、115°

初三上期末综合基础复习题（6）

（一元二次方程、三角形函数、圆相关知识）

1、如果是方程的一个根，则m的值为（　　）

　A、2　　　　B、－2　　　 C、　　　　  D、－

2、二次项系数为1的一元二次方程的两个根分别为和，那么这个方程是（　）

　A、　　　　  B、

　C、　　　　　 D、

3、两根均为负数的一元二次方程是（　　）

　A、　　　　B、

  C、　　　　D、

4．若tan∠a·tan20º=tan45º，则锐角∠a＝（　　　）

（A）20º　　　（B）70º　　　（C）45º　　　（D）30º

5．在△ABC中，∠C＝90º，b＝5，∠A＝23º，则边c为（　　）

6如图，若∠ACB＝90º，CD⊥AB，

AC＝1，AB=5，则cos∠DCB的值（　　　）

7．如图：AB、AC、EF为⊙O的切线，切点分别

为B、C、D，当AB＝10cm时，则△AEF的周长（　　）

（A）15cm　 (B)20CM　 (C)25cm　 (D)30cm

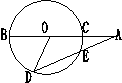8.已知如图：割线AB过点O，且AE等于⊙O的半径，

当∠A＝15°时，则∠BOD＝（　　　）

（A）　　　 30°（B）40°　（C）45°　（D）60°

9．直线y＝kx＋b(k≠0)，且k＜0，b＞0，

则图象不过（　　　）

（A）第一象限　　（B）第二象限　　（C）第三象限　（D）第四象限

10．若∠a为锐角，且，则∠a在（　　）

（A）0º与30º之间　　　（B）30º与45º之间

（C）45º　60º之间　　　（D）60º与90º之间

二、填空题

1.有两个相等的实数根，则k=_________

2.方程的一个根为4，则m=________

3.某产品的原产量为a台，每年的增长率为x% ,两年后的产量为b台，列方程为___________

4．二次三项式为完全平方式，则m＝＿＿＿＿＿＿＿＿

5．与角的两边都相切的圆的圆心的轨迹为＿＿＿＿＿＿＿

6．等腰△ABC中，AB＝AC＝13cm，BC＝24cm，则以顶点A为圆心，半径为＿＿＿cm的圆与线段BC是相切的位置关系。

7．已知P（m＋2，-5）与Q（4，n－3）关于y轴对称，则m＝＿＿，n＝＿＿＿

8．已知y与x＋1成正比例关系，当x＝－3时，y＝5，则列出y与x的

函数关系式为＿＿＿＿＿＿＿

三、已知△ABC中，，∠B＝45º，∠A＝30º，求△ABC的周长？

　　　

四、若方程与均有实根，问与是否有相同的根，若有，请求出这个相同的根，若没有，说明理由。

五、在实数范围内分解因式

二、填空题

1、方程的两根为x₁，x₂，则

2、若方程的根是x=2，则

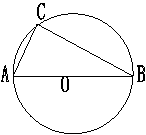
3．已知如图：∠OBA＝27°，则∠C＝＿＿＿＿

4．以－5和3为两根的一个整系数一元二次方程是__________________

5．若tan∠a·tan23º=1，则锐角∠a＝（　　　）

6、在Rt△ABC中，∠C=90°,若tanA=,则sinA等于（　 ）

7、在Rt△ABC中，∠C=90°，tanA=,AC=6,则AB的长为（　 ）

三、在Rt△ABC中，∠C＝90º，，求a、b、c？

四、若方程＝0有两实根，且这两个根的平方和比它们的积大21，求m。

四、解方程　　　　用配方法解方程

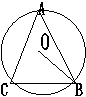
五、已知：如图，AB为⊙O的直径，且当AB=10cm，

AC、BC是方程x²－2(m+2)x+2m²－m+3=0的两个

根（AC﹤BC）。求m的值？

初三上期末综合基础复习题（7）

（一元二次方程、三角形函数、圆相关知识）

1.一个直角△的周长是2+斜边上的中线为1,则此△的面积是(　　  )

  (A)　　　　  (B)1　　　　  (C)2　　　　  (D)

2.∠A为锐角,且cosA=0.2, 则A的取值范围是(　　)

 (A)0°<A£30°　　　　　　　　　 (B)30°<A£45°　

 (C)45°<A£60°　　　　　　　　  (D)60°<A£90°

3、若A为锐角，且，则∠A的值为（　　）

（A）30⁰　（B）45⁰　（C）60⁰　  （D）30⁰或60⁰　

4．一元二次方程经配方后得

A、　B、　 C、　 D、

5．下列语句中，正确的个数是（1）顶点在圆周上的角是圆周角；（2）三点确定一个圆；（3）圆内接四边形中必有两个内角是锐角；（4）垂直于弦的直径必平分弦；（5）如果两条弦相等，那么它们所对的圆心角相等．

A、0个　　　　　B、1个　　　　　C、2个　　　　　D、3个

6．如果用换元法解方程，设，那么原方程可化为A、　 B、　C、　 D、

7．若a、b是方程的根，则的值为

A、1　　　　B、2　　　　C、3　　　　D、4

8．分式方程没有增根，则m的取值为

A、m≠0 B、m≠1　　 C、m≠0或m≠1　　　D、m≠—3且m≠5

9．方程的两根为3，4，那么二次三项式可分解为

　　 　　 　　

13．下列各式中，与tan70°相等的是

A、cot70°　　　B、cot20°　　 C、sin70°　　 D、cos20°

初三上期末综合基础复习题（8）

（一元二次方程、三角形函数、圆相关知识）

1、一元二次方程的两个根中只有一个正根，则（　　）

（A）（B）（C）（D）

2、在△ABC中，∠B=30⁰，AB=，AC=2，则S_△ABC=（　　）

（A）（B）（C）或（D）或

3.如图，AB是⊙O的一条弦，延长AB到C，使BC等于⊙O的半径，连CO并延长交⊙O于D，设　∠ACD=x，∠AOD=y，则x：y=（　　）

（A）1：4  （B）1：3　（C）1：2　（D）1：1

4、当代数式的值为零时，x的值为（　　）

（A）　（B）　（C）　（D）±7

5.已知锐角三角形ABC中则ÐC的度数为(　　)

 (A)30°　　　  (B)45°　　　　  (C)60°　　　 (D)75°

6.已知点A关于x轴的对称点是(a,-2) 关于y轴的对称点是(1,b)那么点A的坐标是(　　）

 (A)(a,-b)　　　　 (B)(b,-a)　　　　  (C)(-2,1)　　　　　 (D)(-1,2)

7、如果是方程的一个根，则m的值为（　　）

　A、-2　　　　B、-3　　　 C、1　　　　  D、2

8、如图，P是圆的直径AB的延长线上一点，PC切这

个圆于C，若∠P=42⁰，则∠BCP=（　　）

（A）26⁰　（B）25⁰　（C）24⁰　（D）23⁰

9、已知方程的两根平方和等于3，则k的值为（　　）

（A）–1或3  （B）–3或1　（C）3  （D）–1

10、Rt△ABC中，∠C=Rt∠，AC=1，BC=2，则sinA=（　　）

（A）2　（B）　（C）　（D）

1.某商品连续两次降价,两次共降了19%,则平均每次降价率为　　　　  ;

2.经过⊙O上任意一点P的弦的中点轨迹为　　　　 　　　　　　　　　　　　　.

3.函数中自变量x的取值范围是　　　　  ;

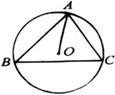
4如图，DABC内接于⊙O，ÐB=ÐOAC，

OA=8cm，则AC=______cm.

5.a为锐角,sin²a+sin²36°=1， 则a=　　　 　　 ctgasin30°=　则a=　　　

6.已知RtDABC中,cosA=,那么,sinA= 　　　 ,tgA=　　　　

7. 若cos(90°-a)=,则ctg(90°-a)=　　　

8．圆内接四边形ABCD中，∠A:∠B:∠C = 4:5:2，则∠D =　　　 ．

9．点A（2m，－3）与点B（－4，－n）关于x轴对称，则m =　　　，n =　　  ．

三、湖北抗洪抢险时，某部队奉命派甲排跑步前往离驻地90千米的公安县抢险，1小时45分后，因险情加重，又增派乙连乘车前往支援。已知乙连比甲排每小时快28千米，恰好在起点全程的处追上甲排。　　　　⑴求乙连的行进速度及追上甲排的时间；

⑵当乙连追上甲排时，上级改令甲排前往离此24千米的石首市执行紧急任务，且要求甲排与乙连同时到达各自的指定地点。试求甲排每小时应加快多少千米？

四、m取什么值时，方程组有唯一实数解？

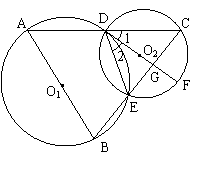五、如图，以△ABC一边AB为直径的⊙O₁过AC的中点D，交BC于点E，⊙O₂为△DEC的外接圆，其直径DF交EC于点G．

（1）求证：∠1=∠2；

（2）已知GE=5，EB=4，求DG的长．

 

 

 

 

 1．的值是　　　　．　　2．直径所对圆周角的度数是　　 ．

3．在实数范围内分解因式　　　　　　　　　　　　．

4．以线段AB为弦的圆的圆心轨迹为　　　　　　　　　　　　　　　　　　

5．直角坐标系中，第四象限的点M到横轴的距离为28，

到纵轴的距离为6，则M点的坐标是___________．

6．如图所示，点I是△ABC的内心，

∠A=56°，则∠BIC=______．

7．已知P是半径为15的⊙O内一点，OP=9，在经过P点的所有弦中，弦长为整数的弦共有______条．

8．在Rt△ABC中，∠C=90°，AC=3，BC=4，若以C为圆心、R为半径所作的圆与斜边AB只有一个公共点，则R的取值是　　　　　　　　　．

三、设x₁，x₂是的两个根，求证：

四.A地某厂共有80人到40千米外的B地施工。现只有一辆可乘40人的汽车，若汽车每小时行35千米，人步行每小时5千米，为尽快到达B地，可让40人先步行，40人乘汽车，汽车开出一段距离后，让车上的人下车步行，汽车立即回头接步行的人开往B地，他们都同时到达B地，问每人乘车多少千米？（汽车调头及工人上下车的时间略去不计）

五.一只船向东北方向以21海里/小时的速度航行,上午8时在M处,测得灯塔P在南偏东75°.上午10时船航行到N处,测得灯塔P在船的正南方向.问在航行过程中,船离灯塔的最短距离是多少?

北

　　　　　  N

　 45°

　

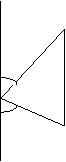
M

　 75°　　　p