数 学 月 考 试 卷 分数
|
1.抛物线y = x2-2x+3的顶点坐标是 。
2.如果函数![]() 中,a>0,b>0,c=0,那么它的图象不经过第 象限。
中,a>0,b>0,c=0,那么它的图象不经过第 象限。
3.把抛物线![]() 向左平移3个单位,再向下平移2个单位后,所得抛物线的解析式为______。
向左平移3个单位,再向下平移2个单位后,所得抛物线的解析式为______。
4、抛物线![]() 的顶点在
的顶点在![]() 轴上,则
轴上,则![]() 的值为
。
的值为
。
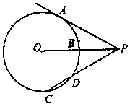 5、抛物线
5、抛物线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,则
,则 ![]() = 。
= 。
6. 等腰梯形ABCD外切于圆,且中位线MN的长是12cm,则梯形ABCD的周长是 。
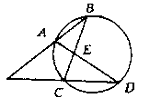
7.如图,AC是⊙O的直径,∠ACB=25° ,PB、PC是⊙O的切 线,C、B为切点, 则∠E= 。
 8.两圆内切时,圆心距为3,其中一个圆半径为8,则另一个圆的半径为
。
8.两圆内切时,圆心距为3,其中一个圆半径为8,则另一个圆的半径为
。
9. 若两圆既存在内公切线,又存在外公切线,那么这两圆的位置关系为 。
 10.
如图,PA切⊙O于点A,PO交⊙O于点B,PDC为割线,如果PB=OB=6,DC=3,那
么PA+PC=
。
10.
如图,PA切⊙O于点A,PO交⊙O于点B,PDC为割线,如果PB=OB=6,DC=3,那
么PA+PC=
。
二.选择题(每小题3分,共30分)
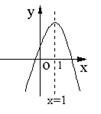
1.二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,
下列结论中,正确的是( )
A.a·c>0 B.b<0 C.b2-4ac<0 D.2a+b=0
 2.在直角坐标系中,函数y= -3x与y=x2-1的图象大致是(
)A.
B.
C.
D.
2.在直角坐标系中,函数y= -3x与y=x2-1的图象大致是(
)A.
B.
C.
D.
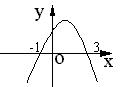 3.已知函数y=ax2+bx+c的图象如图所示,那么此函数的 解析式是( )
3.已知函数y=ax2+bx+c的图象如图所示,那么此函数的 解析式是( )
A.y= - x2+2x+3 B.y =x2-2x-3
C.y= - x2-2x+3 D.y = -x2-2x-3
4.已知P(2,-2)在反比例函数y =![]() 的图象上,那么 函数的解析式为( )
的图象上,那么 函数的解析式为( )
A.y=![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列四个函数中,y随x的增大而减小的是( )
A.y=2x
B.y=![]() C.y=x+1
D.y=x2(x>0).
C.y=x+1
D.y=x2(x>0).
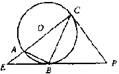
 6. 如图,自圆外一点P引两条割线PAB和PCD, 连结AD、BC相交于E,则下列各式中成立的是( )。
(A)PA·AB=PC·PD (B) AE·BE=CE·DE
6. 如图,自圆外一点P引两条割线PAB和PCD, 连结AD、BC相交于E,则下列各式中成立的是( )。
(A)PA·AB=PC·PD (B) AE·BE=CE·DE
(C) PB·AB=PD·CD (D) PA·BC=PC·AD
7.在以下命题中,正确的为( )
(A)两圆相切,其公切线必垂直连心线;(B)两圆相交,连心线与外公切线相交;(C)连心线是两圆公共的对称轴; (D)两圆无公共点,两圆外离时。
8.两圆相切,圆心距为7cm,小圆半径为3cm,则大圆半径为( )。
(A)10cm (B)4cm (C)10cm或4cm(D)8cm
9.两圆的半径分别为12和 4,外公切线长为 15,则两圆的位置关系是( )
(A)内切 (B)相交 (C)外切 (D)外离
10.两圆的内公切线长为3,半径分别为2√3 和√3 ,则内公切线与连心线的夹角为( ).
(A)30º (B)45º (C)60º (D)90º
三.解答题(每题10分)
1.若二次函数y=mx2-(m-2)x-1的图象与x轴的交点坐标为A(a,0)、B(b,0), 且a+b=ab,试求m的值。
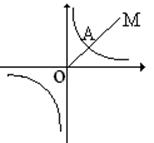 2.如图,在平面直角坐系中,直线y=x与反比例函数的图象在第一象限相交于点A,已知OA的长度是2
2.如图,在平面直角坐系中,直线y=x与反比例函数的图象在第一象限相交于点A,已知OA的长度是2![]() 。
。
(1)求点A的坐标;
(2)求此反比例函数的解析式。
四.计算。(1题8分,2题10分)
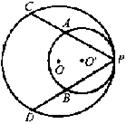 1. 已知:如图,两圆内切于P,大圆弦PC、PD分别交于小圆于A、B两点,
PA=3,AC=2,PB=2,求PD的长。
1. 已知:如图,两圆内切于P,大圆弦PC、PD分别交于小圆于A、B两点,
PA=3,AC=2,PB=2,求PD的长。
2.已知⊙O1、⊙O2的半径分别为15cm和5cm,它们外切于点T,外公切线AB与⊙O1和⊙O2分别切于点A、B,求外公切线的长AB。
五.解答题(本题12分)
二次函数的图象经过![]() 三点:
三点:
(1)求这个函数的解析式
(2)求函数图顶点的坐标
(3)画出函数图象
六. 证明题(本题10分)
⊙O1和⊙O2相交与点B 和C,A是⊙O1上另一点,AT是⊙O1的切线,又 直线AB与AC交⊙O2于点D和E.
求证:AT∥DE.