初三(上)(五·四制)数学期中复习题
一.填空题:
1.当x ________时,![]() 在实数范围内有意义。
在实数范围内有意义。
2.计算:![]() _________;
_________; ![]() =________.
=________.
3.若![]() ,则
,则![]() =__________.
=__________.
4.![]() 的倒数是____________.
的倒数是____________.
5.已知![]() ,化简
,化简![]() =___________.
=___________.
6.若最简二次根式![]() 和
和 ![]() 是同类二次根式,则
是同类二次根式,则![]() ___, b=___.
___, b=___.
7.![]() __________.
__________.
8.![]() 有理化因式是______.
有理化因式是______.
9.![]() __________.
__________.
10. 在实数范围内分解因式:![]() _____.
_____.
11.四边形的四条边AB、BC、CD、DA的长依次为3,4,13,12,又∠CBA是直角,则四边形的面积是 ;
12.一等腰三角形三边的长分别为n2―1,2n,n2+1,(n>1),则它的最大角度数是 ;
13.△ABC中,∠C=90º,两直角边的长分别是3厘米,4厘米,则斜边上的高为 ;
14.己知△ABC的三边分别为a,3,a+2(其中a>1),当a= 时,△ABC是直角三角形;
15.正方形的边长是3,则对角线的长是 ;
16.D是△ABC的BC边的延长线上的一点,且BD=BC+AC,则点C在 的垂直平分线上;
17.在△ABC中,AB=AC=32,DE垂直平分AB于E,交AC于D,若△DBC的周长是56,则BC= ;若BC=21,则△DBC的周长是 ;
18.△ADC中,B是AC边上的一点,AD=BD=BC,若∠C=25º,则∠ADC的外角的度数是 ;
二.选择题:
1.若![]() 应是( )
应是( )
(A)负数 (B)正数 (C)非零实数 (D)有理数
2.![]() 的同类根式是(
)
的同类根式是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.能使![]() 成立的x的取值范围是( )
成立的x的取值范围是( )
(A)![]() (B)
(B)
![]() (C)
(C)![]() (D)
(D) ![]()
4.当![]() 时,化简
时,化简![]() 的结果是(
)
的结果是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.把![]() 化成最简二次根式正确的结果是(
)
化成最简二次根式正确的结果是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.已知![]() ,则x的值等于( )
,则x的值等于( )
(A)4 (B)±2 (C)2 (D)±4
11.等腰三角形一腰上的高与底边的夹角为mº,则这个等腰三角形的顶角的度数是( )
(A)m (B)2m (C)90+m (D)90―m
12.△ABC中,AB=AC,BD平分∠ABC,且∠BDC=75º,则∠A等于( )
(A)30º (B)90º (C)60º (D)45º
|
![]()
 (A)20º (B)15º (C)12.5º (D)10º
(A)20º (B)15º (C)12.5º (D)10º
14.如果一个三角形两边的垂直平分的交点在第三边上,
|
|
|
|
(C)钝角三角形 (D)不能确定
15.如果一个三角形一条边上的中点到其它两边的距离相等,那么这个三角形一定是( )
(A)等边三角形 (B)等腰三角形 (C)不等边三角形 (D)不等腰的钝角三角形
16.若△ABC中,AB=4,AC=6,M是BC的中点,AM=![]() ,则BC的长为( )
,则BC的长为( )
(A)![]() (B)2
(B)2![]() (C)2
(C)2![]() (D)无法计算
(D)无法计算
17.等边三角形的中线的长为a,则边长是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
18.在△ABC中,∠C=90º,AB=m2+n2,BC=m2―n2,(m>n>0),则AC的长是( )
(A)![]() (B)2mn
(C)2m2
(D)2n2
(B)2mn
(C)2m2
(D)2n2
19.四边形的四条边长AB、BC、CD、DA的长分别是2、![]() 、5、4,其中∠B=90º,则四边的面积是( )
、5、4,其中∠B=90º,则四边的面积是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
20.自直角三角形的锐角顶点所引的中线长分别为5和2![]() ,那么斜边的长为( )
,那么斜边的长为( )
(A)10
(B)![]() (C)
(C)![]() (D)
(D)![]()
三.解答题:
1.计算:
(1)![]() (2)
(2)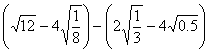
(3)![]() (4)
(4)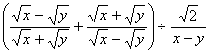
2.已知![]() ,求
,求![]() 的值。
的值。
四.求值:
1.已知![]() ,求
,求![]() 的值。
的值。
2. 己知![]() ,
,![]() ,求
,求![]() 和
和![]() 的值。
的值。
五.证明题:
1.D是等边△ABC内一点,AD=BD,∠DBP=∠DBC,且BP=BA,求∠P的度数。
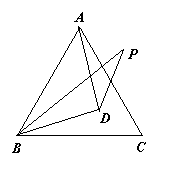 |
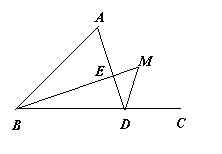 2.28.如图,己知在△ABC中,AB=AC,∠A=90º,M是AB的中点,AE⊥BM于E,延长AE交BC于点D,求证:∠AMB=∠CMD。
2.28.如图,己知在△ABC中,AB=AC,∠A=90º,M是AB的中点,AE⊥BM于E,延长AE交BC于点D,求证:∠AMB=∠CMD。
 |
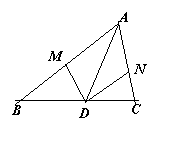
3.AD为△ABC的中线,M在AB上,N在AC上,∠MDN=90º,若BM2+CN2=DM2+DN2,求证:AD2=![]() (AB2+AC2)
(AB2+AC2)
 |
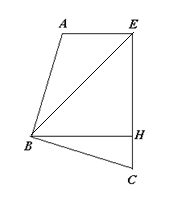
3. 在四边形ABCD中,∠E=90º,AB=BC,BH⊥EC,若BE=4,求四边形ABCD的面积。
 |
