２００６年白云区初中毕业班综合测试（一）
数 学 试 题
本测试题分为选择题和非选择题两部分，共４页；全卷三大题２５小题，满分１５０分。考试时间为１２０分钟。
注意事项：
１．选择题每小题选出答案后，用２Ｂ铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试卷上。
２．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定的区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案，改动的答案也不能超出指定的区域；不准使用铅笔、圆珠笔和涂改液。涉及作图的题目，用２Ｂ铅笔画图。不按以上要求作答的答案无效。
一、选择题（本大题共１０道小题，每小题３分，满分３０分。在每小题给出的四个选择项中，只有一项是符合题目要求的）
１．有理数
在数轴上所表示的点的位置为（ ）
（Ａ）在原点的左侧 （Ｂ）在原点的右侧
（Ｃ）即可在原点的左侧，又可在在原点的右侧 （D）不能确定
２．如果函数y＝kx的图象经过点（－１，３），那么k的值为（ ）
（Ａ）１ （Ｂ）－１ （Ｃ）３ （D）－３
３．足球比赛前，裁判通常要掷一枚硬币来决定比赛双方的场地与首发球者，其主要原因是（ ）
（Ａ）让比赛更富有情趣 （Ｂ）让比赛更具有神秘色彩
（Ｃ）体现比赛的公平性 （D）不知道什么原因
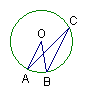
４．如图，Ａ、Ｂ、Ｃ是⊙Ｏ上三点，若∠ＡＣＢ＝２０°，则∠ＡＯＢ的度数为（ ）
（Ａ）１０° （Ｂ）２０° （Ｃ）３０° （D）４０°
５．找出下面与众不同的一个图案（ ）
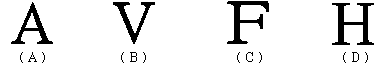
６．如果等腰梯形两底之差等于一腰的长，那么这个等腰梯形的锐角是（ ）
（Ａ）６０° （Ｂ）４５° （Ｃ）３０° （Ｄ）１５°
７．计算结果为
的是（ ）
（Ａ）（x－１）（x＋６） （Ｂ）（x＋１）（x－６）
（Ｃ）（x－２）（x－３） （Ｄ）（x＋２）（x＋３）
８．样本的方差越大，说明（ ）
（Ａ）样本中个体的数量越大 （Ｂ）样本中个体的数量越小
（Ｃ）样本的波动越小 （Ｄ）样本的波动越大
９．如图，已知ＤＥ∥ＢＣ，ＣＤ与ＢＥ相交于点Ｏ，并且Ｓ⊿ＤＯＥ：Ｓ⊿ＣＯＢ＝４：９，则ＡＥ：ＡＣ＝（ ）
（Ａ）４：９ （Ｂ）２：３ （Ｃ）３：２ （Ｄ）９：４
１０．若分式
有意义且它的值为零，其中a、b、c为三角形的三条边，则此三角形为一定为（ ）
（Ａ）等腰三角形 （Ｂ）等边三角形 （Ｃ）各边都不相等的三角形 （Ｄ）直角三角形
二、填空题（本大题共６小题，每小题３分，满分１８分）
１１．抛物线
的开口方向为 ，顶点坐标为
１２．计算
的结果是
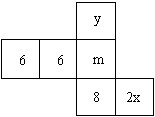
１３．右图是一个正方体的展开图，如果正方体相对的面上标注的值相等，那么x＝ ，y＝
１４．一元二次方程
根的判别式的值为 ，它的两个根分别为x１＝ ， x２＝
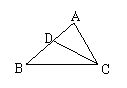
１５．如图，⊿ＡＢＣ中，ＣＤ平分∠ＡＣＢ，∠Ｂ＝４０°，∠ＡＣＢ＝６０°，则∠ＡＤＣ＝
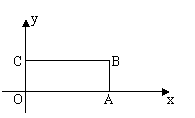
１６．如图，在直角坐标系中，矩形ＯＡＢＣ的顶点Ｏ为坐标原点，顶点Ａ、Ｃ分别在x轴、y轴上，顶点Ｂ的坐标为（１５，６），直线y＝
x＋m恰好将矩形ＯＡＢＣ分成面积相等的两部分，那么m＝
三、解答题（本大题共９小题，满分１０２分．解答应写出文字说明、证明过程或演算步骤）
１７．（本小题满分９分）
计算（结果用根号表示）：
－２cos３０°＋
＋２tan６０°
１８．（本小题满分９分）
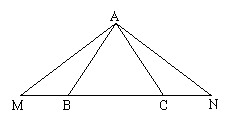
如右图，⊿ＡＢＣ，ＡＢ＝ＡＣ，点Ｍ、Ｎ分别在ＢＣ所在直线上，且ＡＭ＝ＡＮ。
求证：ＢＭ＝ＣＮ
１９．（本小题满分９分）
先化简，再求值：
，其中x＝２
２０．（本小题满分１１分）
设一个三角形的三边长分别为３，１－２m，８，求m的取值范围
２１．（本小题满分１０分）
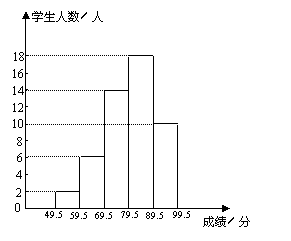
如图，这是某班数学科代表根据他们班上学期的数学成绩画出的频数分布直方图，从这个图中，请你回答下列问题：
（１） 你认为他们班共有学生多少名？
（２） 全班数学成绩及格率（６０分及以上为及格）为多少？
（３） 在哪个分数段的学生最多？
２２．（本小题满分１４分）
请你完成下列问题：
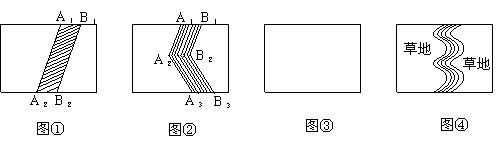
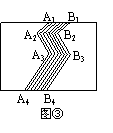
图形的操作过程（本题中四个长方形的水平方向的边长均为a，竖直方向的边长均为b）：在图①中，将线段Ａ１Ａ２向右平移１个单位长度到Ｂ１Ｂ２，得到封闭图形Ａ１Ａ２Ｂ２Ｂ１（即阴影部分）。在图②中，将折线Ａ１Ａ２Ａ３向右平移１个单位长度到Ｂ１Ｂ２Ｂ３，得到封闭图形Ａ１Ａ２Ａ３Ｂ３Ｂ２Ｂ１（即阴影部分）。
（１） 在图③中，请你类似地画一条有两个折点的折线，同样向右平移一个单位长度，从而得到一个封闭图形，并用斜线画出阴影。
（２） 请你分别写出图①、图②、图③中除去阴影部分后剩余部分的面积Ｓ１、Ｓ２、Ｓ３：Ｓ１＝ ，Ｓ２＝ ，Ｓ３＝ 。
（３） 如图④，在一块长方形草地上，有一条弯曲的柏油小路（图中阴影部分），小路任何地方的水平宽度都是１个单位长度，请你猜想空白部分表示的草地面积Ｓ４是多少，并说明你猜想的正确性。
２３．（本小题满分１２分）
在某校举办的足球比赛中规定：胜一场得３分，平一场得１分，负一场得０分。某班足球队参加了１２场比赛，共得２２分。已知这个队只输了２场，那么此队胜几场？平几场？
２４．（本小题满分１４分）
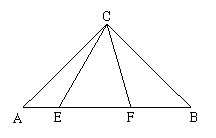
如图，⊿ＡＢＣ是等腰直角三角形，Ｃ是直角顶点。
操作并观察：将三角尺４５°角的顶点与点Ｃ重合，使这个角落在∠ＡＣＢ的内部，两边分别与斜边ＡＢ交于Ｅ、Ｆ（ＣＥ不与ＣＡ重合，ＣＦ不与ＣＢ重合），然后将这个角绕点Ｃ在∠ＡＣＢ内部旋转。
（１）∠ＡＣＥ＋∠ＢＣＦ的度数为多少？
（２）观察点Ｅ、Ｆ的位置发生变化时，ＡＥ、ＥＦ、 ＦＢ中最大线段是否始终是ＥＦ？
（３）探索：ＡＥ、ＥＦ、ＦＢ这三条线段能否组成以ＥＦ为斜边的直角三角形？若能，试给出证明；若不能，请说明理由。
２５．（本小题满分１４分）
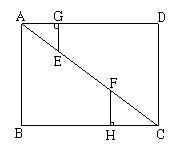
如图，矩形ＡＢＣＤ中，ＡＢ＝３，ＢＣ＝４，线段ＥＦ在对角线ＡＣ上（Ｅ不与Ａ重合，Ｆ不与Ｃ重合），ＥＧ⊥ＡＤ，ＦＨ⊥ＢＣ，垂足分别是Ｇ、Ｈ，且ＥＧ＋ＦＨ＝ＥＦ。
（１）写出图中与⊿ＡＥＧ相似的三角形；
（２）求线段ＥＦ的长；
（３）设ＥＧ＝x，⊿ＡＥＧ与⊿ＣＦＨ的面积和为Ｓ，写出Ｓ关于x的函数关系式及自变量x的取值范围，并求出Ｓ的最小值
 |  |
2006初三“一模”参考答案及评分建议
一、选择题
１．Ｂ ２．Ｄ ３．Ｃ ４．Ｄ ５．Ｃ
６．Ａ ７．Ｃ ８．Ｄ ９．Ｂ １０．Ａ
二、填空题
１１． 向上 （－１，－２） ［第１个空１分，第２个空２分］
１２． 
１３． ３ ８ ［两个空全填对３分，只填对一个空给２分］
１４． １６ －１ ３ ［每个空１分，第２、３空顺序可交换］
１５． ７０°
１６ 
三、解答题
１７．（本小题满分９分）
解：原式＝－１－２×
＋１＋２×
……………………………… ４分
＝－１－＋１＋２……………………………………… ６分
＝……………………………………………………………… ９分
１８．（本小题满分９分）
证法一：由已知条件知，⊿ＡＢＣ和⊿ＡＭＮ
都是等腰三角形（Ａ为共公顶点）…………………………………………… ３分
过点Ａ作ＢＣ所在直线的垂线ｍ，根据“三线合一”定理可知…………… ５分
这两个等腰三角形底边上的中线和顶角的平分线均在ｍ上，
而且这条直线是它们共公的对称轴…………………………………………… ７分
所以Ｂ、Ｃ关于ｍ对称，Ｍ、Ｎ关于ｍ对称，
所以ＢＭ＝ＣＮ（轴对称性质）……………………………………………… ９分
证法二：∵ＡＢ＝ＡＣ，ＡＭ＝ＡＮ
∴∠ＡＢＣ＝∠ＡＣＢ，∠Ｍ＝∠Ｎ（等边对等角）………………………… ３分
∴∠ＡＢＭ＝∠ＡＣＮ（等角的补角相等）…………………………………… ５分
∴∠ＢＡＭ＝∠ＣＡＮ（三角形内角和定理）
在⊿ＡＢＭ和⊿ＡＣＮ中
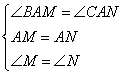……………………………………………………………… ７分
∴⊿ＡＢＭ≌⊿ＡＣＮ（ＡＳＡ）…………………………………………… ８分
∴ＢＭ＝ＣＮ（全等三角形对应边相等）………………………………… ９分
说明：若学生直接用“ＡＡＳ”证全等，也算正确，不扣分。
１９．（本题满分９分）
解：原式＝
…………………………………………………………… ４分
＝
…………………………………………………………………… ６分
当ｘ＝２时………………………………………………………………… ７分
原式＝
……………………………………………………………………… ８分
＝－５……………………………………………………………………… ９分
２０．（本题满分１１分）
解：根据三角形三边关系及已知条件，可得
……………………………………………………… ５分
解（１）得：ｍ＜－２………………………………………………………… ７分
解（２）得：ｍ＞－５………………………………………………………… ９分
∴原不等式组的解集为 －５＜ｍ＜－２
经检验，ｍ的取值范围符合题意……………………………………………… １１分
［最后一句“经检验，ｍ的取值范围符合题意”没有的话，不扣分］
２１．（本题满分１０分）
解：（１）２＋６＋１４＋１８＋１０＝５０
从图中可知，该班共有５０名学生……………………………… ４分
（２）（６＋１４＋１８＋１０）÷５０×１００％＝９６％
全班数学成绩及格率为９６％…………………………………… ７分
（３）从图中可知，８０～９０这个分数段学生最多……………… １０分
２２．（本小题满分１４分）
解：（１）如右图，图画正确，给…………… ３分
（２）Ｓ１＝ 
，Ｓ２＝，Ｓ３＝ …………… ９分
［每个空２分，共６分。解题思路：由长方形和平行四边形的面积公式，得Ｓ１＝ab－b。在图②中，过Ａ２、Ｂ２作直线，把原图形分割成上下两部分（长仍为a，宽分别为b１、b２，且b１＋b２＝b），则有Ｓ２＝（ab１－b１）＋（ab２－b２）＝a（b１＋b２）－（b１＋b２）＝ab－b，对于有两个折点的图形，同样可以分割成三部分，同理可求得Ｓ３＝ab－b；］
（３）Ｓ４＝ …………………………………………………………… １１分
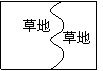结合（２）中的三种情况，可以猜想原题图④中草地的面积应为Ｓ４＝ab－b。其理由是：把左侧草地向右平移一个单位（相当于把阴影部分挖去，如图所示），则小路左右边线重合，两块草地便拼成一个宽为b，长为（a－１）的长方形，当然面积为b（a－１），即ab－b
…………………………………………………………………………… １４分
２３．（本小题满分１２分）
解：设该队胜x场，平y场…………………………………………………… １分
根据题意，可得
…………………………………… ７分
解该二元一次方程组，得
…………………………………………… １１分
答：此队胜６场，平４场。
２４．（本小题满分１４分）
解：（１）∠ＡＣＥ＋∠ＢＣＦ＝４５°………………………………………… ２分
（２）是………………………………………………………………………… ５分
（３）能………………………………………………………………………… ６分
证明：把⊿ＣＢＦ绕点Ｃ顺时针旋转９０°得⊿ＣＡＧ
使ＣＢ与ＣＡ重合，连结ＧＥ………………………………………………… ９分
根据旋转性质，∠ＡＣＧ＝∠ＢＣＦ，ＡＧ＝ＢＦ，ＣＧ＝ＣＦ
∴∠ＥＣＧ＝∠ＥＣＡ＋∠ＡＣＧ＝∠ＥＣＡ＋∠ＢＣＦ＝４５°……… １１分
在⊿ＥＣＧ和⊿ＥＣＦ中
∴⊿ＥＣＧ≌⊿ＥＣＦ中
∴ＥＧ＝ＥＦ…………………………………………………………………… １３分
∵∠ＧＡＣ＝∠Ｂ＝４５°
∴∠ＧＡＥ＝∠ＧＡＣ＋∠ＣＡＥ＝４５°＋４５°＝９０°
∴⊿ＧＡＥ是以ＧＥ为斜边的直角三角形，而ＧＥ＝ＥＦ，ＡＧ＝ＢＦ
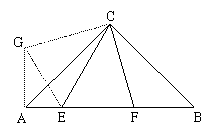∴ＡＥ、ＥＦ、ＦＢ能组成以ＥＦ为斜边的直角三角形…………………… １４分
２５．（本小题满分１４分）
解：（１）与⊿ＡＥＧ相似的三角形分别为：
⊿ＡＣＤ、⊿ＣＦＨ、⊿ＡＣＢ…………………………………… ３分
（２）在Ｒｔ⊿ＡＢＣ中，ＡＢ＝３，ＢＣ＝４，
ＡＣ＝
＝５…………………………………………… ４分
由⊿ＡＥＧ∽⊿ＡＣＤ得
，得ＡＥ＝
ＧＥ
同理得ＣＦ＝ＦＨ………………………………………………… ６分
ＡＥ＋ＥＦ＋ＦＣ＝ＡＣ，
即ＧＥ＋ＥＦ＋ＦＨ＝５，
（ＧＥ＋ＦＨ）＋ＥＦ＝５
∵ＥＧ＋ＦＨ＝ＥＦ，∴ＥＦ＋ＥＦ＝５，
ＥＦ＝
……………………………………………………………… ８分
（３）若ＥＧ＝x，∵⊿ＡＥＧ∽⊿ＡＣＤ
∴
，即
，得ＡＧ＝
x…………………… ９分
由ＥＧ＋ＦＨ＝ＥＦ
得ＦＨ＝ＥＦ－ＥＧ＝－x
又由⊿ＣＦＨ∽⊿ＣＡＢ，
同理可得ＣＨ＝（－x）…………………………………… １０分
Ｓ＝Ｓ⊿ＡＥＧ＋Ｓ⊿ＣＦＨ
＝ＡＧ·ＥＧ＋ＣＨ·ＦＨ
＝·x·x＋·（－x）·（－x）
＝
………………………………………………… １２分
其中自变量x的取值范围为０＜x＜………………………… １３分
通过配方，Ｓ＝
∴Ｓ的最小值为
……………………………………………… １４分