北京市朝阳区初三年级综合练习(一)
数学试卷
第I卷(共44分)
考生须知:
1. 第I卷为选择题,只有一道大题,共2页。答题前要认真审题,看清题目要求,按要求认真作答。
2. 第I卷各题均须按规定要求在“机读答题卡”上作答,题号要对应,填涂要规范。
一. 选择题(共11个小题,每小题4分,共44分)
下列各题均有四个选项,其中只有一个是符合题意的。用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑。
1. -5的绝对值是
A. 5 B. ![]() C.
C.
![]() D.
D.
![]()
2. 下列运算中正确的是
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 某市中心广场的面积约为440000平方米,440000用科学记数法可表示为
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
4. 在线段、角、正三角形、平行四边形、菱形中,是中心对称图形的有
A. 1个 B. 2个 C. 3个 D. 4个
5. 点P(-2,5)关于x轴的对称点的坐标是
A. (-2,-5) B. (2,-5)
C. (5,-2) D. (2,5)
6. 函数![]() 中自变量x的取值范围是
中自变量x的取值范围是
A. x>1 B. ![]() C.
C.
![]() D.
D.
![]() 且
且![]()
7. 如图,已知点A在反比例函数的图象上,那么该反比例函数的解析式为
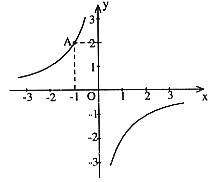
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
8. 如果两个圆的半径分别为2和3,圆心距为1,那么这两个圆的位置关系是
A. 外离 B. 外切 C. 相交 D. 内切
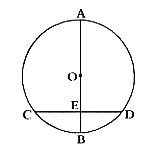
9. 如图,AB是⊙O的直径,弦![]() ,垂足是E,如果AB=10,EB=2,那么CD的长是
,垂足是E,如果AB=10,EB=2,那么CD的长是
A. 8 B. 4 C. 6 D. 5
10. 如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
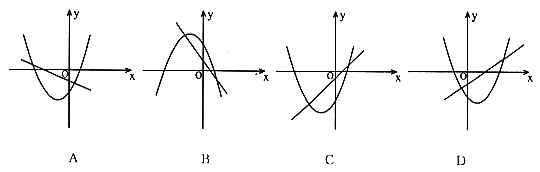
11. 函数![]() 与
与![]() 在同一平面直角坐标系中的图象可能是
在同一平面直角坐标系中的图象可能是
第II卷(共76分)
考生须知:
1. 考生要认真填写密封线内的区(县)名、学校名、姓名、考号。
2. 第II卷包括七道大题,共7页。答题前要认真审题,看清题目要求,按要求认真作答。
3. 答题时字迹要工整,画图要清晰,卷面要整洁。
4. 除画图可以用铅笔外,答题必须用黑色或蓝色钢笔、圆珠笔。
二. 填空题(共5小题,每小题4分,共20分)
12. 一组数据2,5,3,x的平均数为3,则2,5,3,x的方差是__________
13. 已知在![]() 中,
中,![]() ,那么
,那么![]() __________
__________
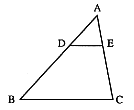
14. 如图,![]() 中,点D、E分别在AB、AC边上,且DE//BC,AD:DB=1:2,那么
中,点D、E分别在AB、AC边上,且DE//BC,AD:DB=1:2,那么![]() 和
和![]() 的周长比是__________
的周长比是__________
15. 正六边形对边之间的距离为12,则它的边长是__________
16. 用“·”和“-”按一定规律组成下面的图形。请你用n(n是正整数)的代数式分别表示第n图中“·”和“-”的个数,分别是__________、__________。
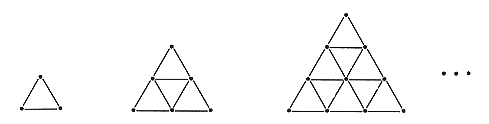
第1图 第2图 第3图
三. (共3个小题,共16分)
17. (本小题满分5分)
分解因式:![]()
18. (本小题满分5分)
计算:![]()
19. (本小题满分6分)
用换元法解方程:![]()
四. (共2个小题,共11分)
20. (本小题满分5分)
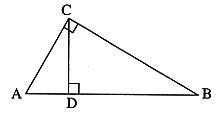
已知:如图,在![]() 中,
中,![]() ,垂足是D,若AC=4,BD=6,求BC的长。
,垂足是D,若AC=4,BD=6,求BC的长。
21. (本小题满分6分)
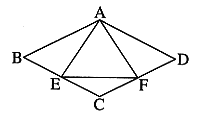
已知:如图,在菱形ABCD中,E、F分别是BC和CD的中点,求证:![]()
五. (本题满分6分)
22. 列方程或方程组解应用题:
某公园的门票价格如下表:
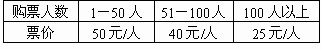
我区某校初三年级(1)、(2)两班共有学生100多人,其中(1)班50多人,(2)班不足50人,准备去此公园游览。若两班分别购票共需4730元;若两班合在一起购票共需2650元。请问初三(1)、(2)两班各有学生多少名?
六. (本题满分7分)
23. 如果关于x的方程![]() ①
①
和![]() ②都有两个不相等的正整数根,求m、n的整数值。
②都有两个不相等的正整数根,求m、n的整数值。
七. (本题满分8分)
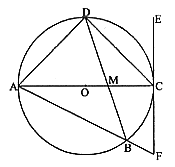
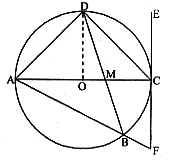
24. 已知:如图,AC是⊙O的直径,点D为![]() 的中点,
的中点,![]() ,点F为EC延长线上一点,AF交⊙O于点B,且FB:AB=1:4,连结DB,交AC于点M,四边形ADCF的面积为50。求:
,点F为EC延长线上一点,AF交⊙O于点B,且FB:AB=1:4,连结DB,交AC于点M,四边形ADCF的面积为50。求:
(1)⊙O的半径长。
(2)DB的长。
八. (本题满分8分)
25. 已知:直线![]() 过点C(4,m)、D(n,
过点C(4,m)、D(n,![]() )和F(
)和F(![]() ,0),如果m、n是方程
,0),如果m、n是方程![]() 的两个根
的两个根
(1)求直线CD的解析式
(2)若抛物线![]() 过点C、D,顶点为M,与x轴交于点A、B(点A在点B的左边)
过点C、D,顶点为M,与x轴交于点A、B(点A在点B的左边)
①求此抛物线的解析式
②在直线CM上是否存在点P,使得![]() ?若存在,求点P的坐标;若不存在,说明理由。
?若存在,求点P的坐标;若不存在,说明理由。
![]()
【试题答案】
北京市朝阳区初三年级综合练习(一)
数学试卷答案及评分标准
一. 选择题(共11个小题,每小题4分,共44分)
1. A 2. B 3. C 4. C 5. A 6. D
7. B 8. D 9. A 10. C 11. D
二. 填空题(共5个小题,每小题4分,共20分)
12. ![]() 13.
13.
![]() 14.
1:3 15.
14.
1:3 15. ![]()
16. ![]() 、
、![]()
三. (共3个小题,共16分)
17. (本小题满分5分)
分解因式:![]()
解:![]()
![]() 1分
1分
![]() 3分
3分
![]() 5分
5分
18. (本小题满分5分)
计算:![]()
解:![]()
![]() 3分
3分
![]() 4分
4分
![]() 5分
5分
19. (本小题满分6分)
用换元法解方程:![]()
解:![]()
设![]() ,原方程化为
,原方程化为![]() 1分
1分
解得![]() 3分
3分
当![]() 时,
时,![]()
![]()
解得![]() ,
,![]() 4分
4分
当![]() 时,
时,![]()
![]()
![]() ,这个方程无实数解 5分
,这个方程无实数解 5分
经检验,![]() 都是原方程的解 6分
都是原方程的解 6分
四. (共2个小题,共11分)
20. (本小题满分5分)
已知:如图,在![]() 中,
中,![]() ,垂足是D,若AC=4,BD=6,求BC的长。
,垂足是D,若AC=4,BD=6,求BC的长。
解:![]() 中,
中,![]()
![]()
![]() 2分
2分
![]()
![]()
![]()
AB=8或AB=-2
![]() (舍去)
(舍去)
![]() 4分
4分
在![]() 中,
中,![]()
![]() (只取正根) 5分
(只取正根) 5分
21. (本小题满分6分)
已知:如图,在菱形ABCD中,E、F分别是BC和CD的中点,求证:![]()
证明:![]() 四边形ABCD是菱形
四边形ABCD是菱形
![]() 1分
1分
![]() E、F分别是BC和CD的中点
E、F分别是BC和CD的中点
![]()
![]() 2分
2分
在![]() 和
和![]() 中
中
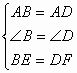
![]() 4分
4分
![]() 5分
5分
![]() 6分
6分
五. (本题满分6分)
22. 列方程或方程组解应用题:
某公园的门票价格如下表:
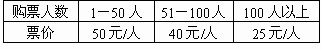
我区某校初三年级(1)、(2)两班共有学生100多人,其中(1)班50多人,(2)班不足50人,准备去此公园游览。若两班分别购票共需4730元;若两班合在一起购票共需2650元。请问初三(1)、(2)两班各有学生多少名?
解:设初三(1)班有学生x人,初三(2)班有学生y人 1分
据题意,可列出方程组![]() 3分
3分
解得![]() 5分
5分
答:初三(1)班有学生57人,初三(2)班有学生49人。 6分
六. (本题满分7分)
23. 如果关于x的方程![]() ①
①
和![]() ②
②
都有两个不相等的正整数根,求m、n的整数值。
解:(1)设![]() 分别为方程①和②的两个实数根
分别为方程①和②的两个实数根
据题意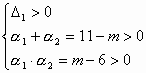
![]()
![]()
![]() 为整数,
为整数,![]() 7、8、9、10
7、8、9、10
当m=7时,方程①的根不是整数
当m=9或10时,方程①无实数根
当m=8时,![]()
方程①为![]()
![]() 3分
3分
(2)方程②可化为![]()
![]()
![]()
![]() 方程②的两个根分别为
方程②的两个根分别为![]()
![]() 方程②有两个正整数根,且n为整数
方程②有两个正整数根,且n为整数
![]() 1、2、3、4、6、12
1、2、3、4、6、12
并且![]() 1、2、3、6
1、2、3、6
![]() 0、1、2、3、5、11
0、1、2、3、5、11
并且![]() 2、3、4、7
2、3、4、7
![]() 或3
或3
又![]()
![]() 6分
6分
综合(1)(2)![]() 7分
7分
七. (本题满分8分)
24. 已知:如图,AC是⊙O的直径,点D为![]() 的中点,
的中点,![]() ,点F为EC延长线上一点,AF交⊙O于点B,且FB:AB=1:4,连结DB,交AC于点M,四边形ADCF的面积为50。求:
,点F为EC延长线上一点,AF交⊙O于点B,且FB:AB=1:4,连结DB,交AC于点M,四边形ADCF的面积为50。求:
(1)⊙O的半径长。
(2)DB的长。

解:(1)![]() AC是⊙O的直径,
AC是⊙O的直径,![]()
![]() D为
D为![]() 的中点,
的中点,![]()
![]()
![]()
![]()
![]() AC为⊙O的直径
AC为⊙O的直径
![]() EF切⊙O于C
EF切⊙O于C
![]()
![]()
![]() 设
设![]()
![]()
在![]() 中
中
![]()
![]()
![]()
在![]() 中
中
![]()
![]()
![]()
![]()
![]()
![]()
![]()
即⊙O的半径长为5 3分
(2)连结OD,![]()
![]()
![]()
又![]()
![]()
![]()
设![]()
![]()
![]() ①
①
![]() 为等腰直角三角形,
为等腰直角三角形,![]()
![]()
在![]() 中,
中,![]()
![]() ②
②
由①②解得![]()
![]() 舍去
舍去
![]()
![]()
![]()
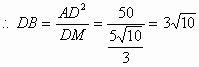 8分
8分
八. (本题满分8分)
25. 已知:直线![]() 过点C(4,m)、D(n,
过点C(4,m)、D(n,![]() )和F(
)和F(![]() ,0),如果m、n是方程
,0),如果m、n是方程![]() 的两个根
的两个根
(1)求直线CD的解析式
(2)若抛物线![]() 过点C、D,顶点为M,与x轴交于点A、B(点A在点B的左边)
过点C、D,顶点为M,与x轴交于点A、B(点A在点B的左边)
①求此抛物线的解析式
②在直线CM上是否存在点P,使得![]() ?若存在,求点P的坐标;若不存在,说明理由。
?若存在,求点P的坐标;若不存在,说明理由。
解:(1)![]() 直线CD过点C(4,m)、D(n、
直线CD过点C(4,m)、D(n、![]() )、F(
)、F(![]() ,0)
,0)
![]()
又m、n为方程![]() 的两个根,
的两个根,![]()
解得![]()
![]() 直线CD的解析式为
直线CD的解析式为![]() 3分
3分
(2)①依题意,得![]()
又![]() ,代入
,代入![]()
得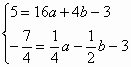
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() 5分
5分
②答:存在点P,使![]() 。解答如下:
。解答如下:
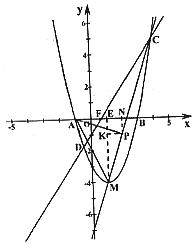
设直线CM的解析式为![]()
![]() 抛物线的顶点为M(1,-4),又C(4,5)
抛物线的顶点为M(1,-4),又C(4,5)
![]()
解得![]()
![]() 直线CM的解析式为
直线CM的解析式为![]()
![]() 点P在直线CM上,
点P在直线CM上,![]() 设点P的坐标为(x,3x-7)
设点P的坐标为(x,3x-7)
![]() 抛物线
抛物线![]() 与x轴交于A、B两点(点A在点B的左边)
与x轴交于A、B两点(点A在点B的左边)
![]() A(-1,0)
A(-1,0)
如图,过点P作![]() 轴于N,过点M作
轴于N,过点M作![]() 轴于E,过点P作
轴于E,过点P作![]() 于K
于K
在![]() 中,
中,![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
![]()
解得![]()
![]() P(2,-1) 8分
P(2,-1) 8分