北京市东城区2005年初三年级综合练习(二)
初三数学
考生须知:
1. 本试卷分为第I卷(选择题)和第II卷(填空题、解答题)两部分,共8页。
2. 认真填写第1、5页密封线内的学校、姓名和报名号。
3. 考试结束,将试卷和机读答题卡一并交回。
第I卷(选择题44分)
注意事项:
考生要按要求在机读答题卡上作答,题号要对应,填涂要规范。
一. 选择题:本题共11个小题,每小题4分,共44分。在每小题给出的四个选项中,只有一个是符合题目要求的。
1. ![]() 的相反数是
的相反数是
A. ![]() B.
B.
![]() C.
3 D. -3
C.
3 D. -3
2. 据有关资料显示,全球的森林覆盖面积正以每年公顷的速度沙漠化,用科学记数法表示成
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 小明做了4个练习题:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
根据你的判断,小明做对的题的个数是
A. 1个 B. 2个 C. 3个 D. 4个
4. 函数![]() 的自变量x的取值范围是
的自变量x的取值范围是
A. ![]() B.
B.
![]() 且
且![]() C.
C.
![]() D.
D.
![]()
5. 下列各图均是由四个边长为1的小正方形构成的大正方形,其中阴影面积最大的是
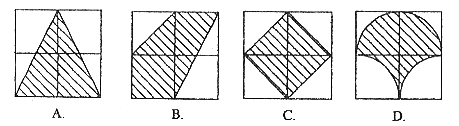
6. 为了判断甲、乙两个小组学生英语口语测验成绩哪一组比较整齐,通常需要知道两组成绩的
A. 平均数 B. 众数 C. 中位数 D. 方差
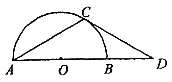
7. 如图,⊙O是![]() 的外接圆,AD是切线,BC的延长线交AD于点D,
的外接圆,AD是切线,BC的延长线交AD于点D,![]() ,
,![]() ,则
,则![]() 的度数为
的度数为
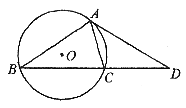
A. 25° B. 30° C. 35° D. 40°
8. 一次函数![]() 的图象既不经过第二象限,也不经过原点,则k、b的取值范围是
的图象既不经过第二象限,也不经过原点,则k、b的取值范围是
A. k<0,b<0 B. k>0,b>0
C. k>0,b<0 D. k<0,b>0
9. 下列命题中正确的是
A. 一个角的补角是一个钝角 B. 有两个角相等的梯形是等腰梯形
C. 圆心角是圆周角的2倍 D. 顶角相等的两个等腰三角形相似
10. 某书店4月份营业额为2.2万元,5月份营业额为2.42万元。如果保持同样的增长率,6月份应完成营业额
A. 2.64万元 B. 2.662万元 C. 2.724万元 D. 2.86万元
11. 4张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到如图(2)所示,那么她所旋转的牌从左起是
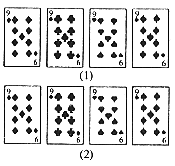
A. 第一张 B. 第二张 C. 第三张 D. 第四张
第II卷(填空题20分,解答题56分)
注意事项:
第II卷包括两道大题。除作图可以用铅笔以外,考生必须用蓝色或黑色的钢笔或圆珠笔在本卷上作答。
二. 填空题:本大题共5小题,每小题4分,共20分。把答案填在题中的横线上。
12. 因式分解:![]() ____________
____________
13. 点A(1,a)在函数![]() 的图象上,则点A关于y轴的对称点B的坐标是____________。
的图象上,则点A关于y轴的对称点B的坐标是____________。
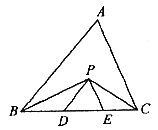
14. 如图,在![]() 中,BC=5cm,BP、CP分别是
中,BC=5cm,BP、CP分别是![]() 和
和![]() 的角平分线,且PD//AB,PE//AC,则
的角平分线,且PD//AB,PE//AC,则![]() 的周长是__________cm。
的周长是__________cm。
15. 如图,AB是半圆O的直径,点D在AB的延长线上,且BD=OB,点C在⊙O上,![]() ,根据以上信息,写出两个正确结论:①________________;②_______________
,根据以上信息,写出两个正确结论:①________________;②_______________
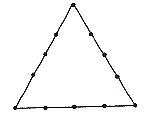
16. 一个由12个人表演的团体舞蹈要摆出三条直线的造型,其中每条直线上恰好有5个人。如图所示就是一种符合要求的造型,请你再设计出两种符合要求的不同的造型。
三. 解答题:本大题共9小题,共56分。解答应写出文字说明、证明过程或演算步骤。
17. (本题5分)
计算:![]()
18. (本题5分)
已知![]() ,求
,求![]() 的值。
的值。
19. (本题6分)
解方程:![]()
20. (本题5分)
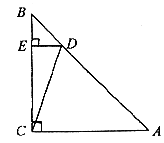
如图,已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,D是AB上一点,AD=3DB,过点D作
,D是AB上一点,AD=3DB,过点D作![]() 于点E,连结CD,求
于点E,连结CD,求![]() 的值。
的值。
21. (本题6分)
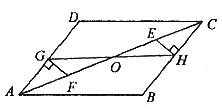
已知:如图,在平行四边形ABCD中,E、F是对角线AC上的两个点,且![]() 于H,
于H,![]() 于G,连结GH,交AC于点O。
于G,连结GH,交AC于点O。
(1)请你再添加一个条件,使GH与EF互相平分,并写出证明过程。
(2)你还能再找出一个与你添加的条件有关的结论吗?如果有,请直接写出来。
22. (本题6分)
银行储蓄存款,按存入当日的利率计息,而且一般存款均需纳税,税款为利息的20%。2004年11月1日开始人民币定期存款利息上调,五年定期存款年利率由2.79%上调到3.6%。设本金x元,在调息之前和调息之后分别存入五年定期,所得税后利息之差为y元。
(1)请写出y与x的函数关系式;
(2)调息之后刘先生将4万元现金存成五年定期,这样他比调息之前存会多得多少利息?
23. (本题7分)
已知关于x的方程![]() ①的两个实数根的倒数和等于3,且关于x的方程
①的两个实数根的倒数和等于3,且关于x的方程![]() ②有实数根,又k为正整数,求代数式
②有实数根,又k为正整数,求代数式![]() 的值。
的值。
24. (本题8分)
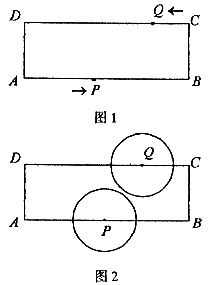
如图1,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A-B-C-D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s)。
(1)当t为何值时,四边形QPBC为矩形?
(2)如图2,如果⊙P和⊙Q的半径都是5cm,那么t为何值时,⊙P和⊙Q相切?
25. 本题8分
已知抛物线![]() 交x轴于两点A(x1,0)、B(x2,0)(
交x轴于两点A(x1,0)、B(x2,0)(![]() ),交y轴于点C,且OA-OB=4。
),交y轴于点C,且OA-OB=4。
(1)试确定抛物线和直线BC的解析式;
(2)若⊙P为![]() 的外接圆,求此圆的半径r;
的外接圆,求此圆的半径r;
(3)在对称轴左侧的抛物线上是否存在点D,使得直线PD交⊙P的弦BC于点M,并有![]() ?若存在,求出D点坐标;若不存在,请说明理由。
?若存在,求出D点坐标;若不存在,请说明理由。
![]()
【试题答案】
北京市东城区2005年初三年级综合练习(二)
初三数学参考答案
一. 选择题(每小题4分,共44分)
1. B 2. C 3. A 4. D 5. B 6. D
7. C 8. C 9. D 10. B 11. A
二. 填空题(每小题4分,共20分)
12. ![]()
13. (-1,3)
14. 5
15. CD是半圆O的切线;![]() 是等腰三角形;CA=CD;
是等腰三角形;CA=CD;![]() ;
;![]() ;
;![]() 为
为![]() ;
;![]() 为
为![]() ;
;![]() 等任写两个。
等任写两个。
16. 画对一个给2分。
三. 解答题(共56分)
17. (本题5分)
计算:![]()
解:![]() 2分
2分
![]() 4分
4分
=3 5分
18. (本题5分)
已知![]() ,求
,求![]() 的值。
的值。
解:由已知,得![]() ,则
,则
![]() 2分
2分
![]() 3分
3分
![]() 4分
4分
=1 5分
19. (本题6分)
解方程:![]()
解:设![]() ,则
,则![]() 2分
2分
原方程化成![]() 3分
3分
解这个方程,得![]() 4分
4分
当y=1时,![]() ,即
,即![]() 。由
。由![]() 知,此方程无实根
知,此方程无实根
5分
当y=-2时,![]() ,即
,即![]()
解得![]()
经检验,x=-1是原分式方程的解。
![]() 原方程的解为x=-1 6分
原方程的解为x=-1 6分
20. (本题5分)
解:![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]()
![]() DE//AC
DE//AC
![]() ,
,![]() 也是等腰直角三角形 2分
也是等腰直角三角形 2分
![]()
![]() 3分
3分
设![]() ,则
,则![]() ,
,![]() 4分
4分
![]() 5分
5分
21. (本题6分)
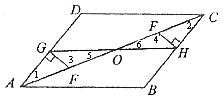
(1)GF=HE;AF=CE;AG=CH等均可。此步正确给2分;证明正确给到5分
以证明GF=HE为例,其它情况相应给分
证明:在平行四边形ABCD中,AD//BC
![]()
![]() 于H,
于H,![]() 于G,
于G,![]()
![]()
![]() 分别是
分别是![]() 和
和![]() 的外角
的外角
![]() ,
,![]()
![]() 3分
3分
在![]() 和
和![]() 中
中
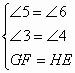 4分
4分
![]()
![]()
![]() 与EF互相平分 5分
与EF互相平分 5分
(2)AF=CE,AG=CH等写出一个即可。此空1分
22. (本题6分)
解:(1)![]() 2分
2分
![]() 4分
4分
(2)当![]() 时,
时,![]() (元) 5分
(元) 5分
答:刘先生在调息之后把4万元存成五年定期,比他在调息之前存将多得1296元。
6分
23. (本题7分)
解:设方程①的两个实数根分别为x1、x2
则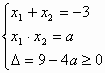 1分
1分
由条件,知![]() 2分
2分
即![]() ,且
,且![]()
故a=-1 3分
则方程②为![]()
当![]() 时,
时,![]() 。则
。则![]() 4分
4分
当![]() 时,
时,![]() ,
,![]() 5分
5分
又![]() 是正整数,且
是正整数,且![]() ,则
,则![]() ,但使
,但使![]() 无意义 6分
无意义 6分
综上,代数式![]() 的值为0 7分
的值为0 7分
24. (本题8分)
解:(1)在矩形ABCD中,AB=24cm,BC=8cm
依题意,PB=CQ,即![]() ,
,![]() 1分
1分
即当运动时间t为4s时,四边形QPBC为矩形 2分
(2)![]() ⊙P和⊙Q的半径都是5cm,若⊙P和⊙Q外切,则圆心距
⊙P和⊙Q的半径都是5cm,若⊙P和⊙Q外切,则圆心距![]()
3分
①点P在AB上
当⊙P在⊙Q的左侧时(如图1),作![]() 于点E
于点E
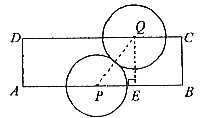
图1
有![]()
![]()
即![]() ,则
,则![]() 4分
4分
当⊙P在⊙Q的右侧时,同理有![]() ,则
,则![]() 5分
5分
②点P在BC上
当点P在B点时,![]() ,则CQ=12
,则CQ=12
![]()
故⊙P与⊙Q相离
![]() 当点P在BC上时,⊙P与⊙Q不会相切 6分
当点P在BC上时,⊙P与⊙Q不会相切 6分
③点P在CD上
当⊙P在⊙Q的右侧时(如图2),有![]()
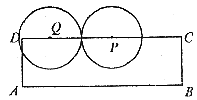
图2
即![]() ,则
,则![]() 7分
7分
当![]() 时,点Q到达点D,点P也随之停止,不会再有⊙P与⊙Q相切
时,点Q到达点D,点P也随之停止,不会再有⊙P与⊙Q相切
综上,当运动时间分别为3s、5s、11s时,⊙P与⊙Q相切 8分
25. (本题8分)
解:(1)由已知抛物线![]() 交x轴于两点A(x1,0)、B(x2,0)(
交x轴于两点A(x1,0)、B(x2,0)(![]() )
)
![]() ,
,![]() 1分
1分
![]()
![]()
![]() ,而
,而![]()
![]()
![]()
![]()
![]() ,则a=1 2分
,则a=1 2分
![]() 抛物线为
抛物线为![]() 3分
3分
![]() A(-5,0),B(1,0)
A(-5,0),B(1,0)
又![]() 此抛物线交y轴于点C(0,-5),设直线BC的解析式为
此抛物线交y轴于点C(0,-5),设直线BC的解析式为![]()
![]()
解得![]()
![]() 直线BC的解析式为
直线BC的解析式为![]() (如图) 4分
(如图) 4分
(2)由(1)知,抛物线的对称轴为![]() ,且
,且![]() 是等腰直角三角形
是等腰直角三角形
![]() 点P在AC的垂直平分线
点P在AC的垂直平分线![]() 上,即P(-2,-2)
上,即P(-2,-2)
![]() ⊙P的半径
⊙P的半径![]() 6分
6分
(3)设存在满足条件的点D,连结直线PD交BC于点M
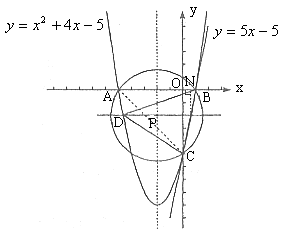
要使![]() ,只要
,只要![]()
作![]() 轴于点N
轴于点N
![]()
![]()
![]()
![]()
![]() 点P到x轴的距离为2
点P到x轴的距离为2
![]() PM//AB
PM//AB
![]() PD所在直线为
PD所在直线为![]() 7分
7分
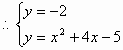
解得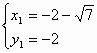 ,
,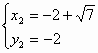 (舍去)
(舍去)
![]() D(
D(![]() )为所求 8分
)为所求 8分