初三教学质量调查卷

（时间100分，总分150分）

一、选择题：（本题12小题，每小题4分，共48分）

1、在下列实数中，无理数是　 （　　 ）

(A) 3.14　　　(B)　　  (C)0　　  (D)

2、若反比例函数的图象经过点（2，-3），那么k的值为（　　 ）

(A) -6　　　　(B) 6　　　 (C)　　(D) 　　 

3、下列运算正确的是　　　（　　 ）

(A) a⁶÷a²=a³　　　(B)(a²) ³=a⁵　　 (C)a²·a³=a⁵　　(D)a⁶-a²=a⁴

4、如图，四边形ABCD内接于⊙O，若∠BOD=140⁰，则∠BCD =（　　 ）

(A)140°　　　 (B)110°　　　  (C)70°　　　　  (D)20°

　　　　　 3x＋1＜0　　

5、不等式组　－x ＜3　  的解是（　　　）

(A) x＞　　(B)－3＜x＜　　(C) x＜－3　　(D) x＞或x＜－3

6、从1到9这九个自然数中任取一个数是2的倍数或是3的倍数的概率是（　　 ）　 (A) 　　　(B) 　　　 (C) 　　　 (D)

7、已知圆台的轴截面中位线为10，母线长为8，则圆台的侧面积为 （　　）(A) 40　　　(B)40∏　　　 (C) 80∏　　　 (D)160∏

8、已知一元二次方程x²－3x+4=0，下列说法正确的是（　　　）

(A)两根之和为3，两根之积为4　　　(B)两根之和为－3，两根之积为4　

(C)两根之和为3，两根之积为－4　　 (D) 以上均不对

9、下列每张方格纸上都画有一个圆，只用不带刻度的直尺就能确定圆心位置的是（　　）

　　　

.　　　　　 (A)　　　　　  (B)　　　　　　 (C)　　　　　　  (D)

10、以下各组字母和汉字中，既是轴对称又是中心对称的一组是 （　　 ）

(A)W,O,E,申　  (B)A,M,O,干　　(C)H,O,X,田　  (D)N,H,O,中

11、一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为　（　　　）

(A) 　(B) 　(C)4　 (D)　　　　 

12、如上图，向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽，水槽中水面上升高度h与注水时间t之间的函数关系，大致是下列图象中的 （　　 ）

　　 　　.　

(A)　　　　　　  (B)　　　　　  　　(C)　　　　　　　 (D)

二、填空题：（本题有6小题，每小题5分，共30分）

13、截止2003年5月8日止，国家民政部收到各界人士抗非典捐款元，用科学计数法表示为_____________.

14、在⊿ABC中，已知∠BAC=90°，AD⊥BC于D，AD=5,现欲求BC的长，条件不充分，请加一个条件____________（只需填一个），并求出此时BC=________.

15、已知.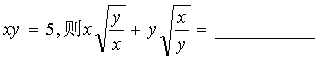

16、若⊿ABC中，DE∥BC交AB于E,DF∥AB交BC于F，若⊿AED的面积为27，⊿CDF的面积为12，则四边形BFDE的面积为___________

17、在平坦的草地上有A、B、C三个小球，若已知A球和B球相距3米，A球与C球相距1米，则B球与C球可能相距____________米，（球的半径忽略不计，只要求填出3个符合条件的数）

18、根据指令[S，A]（S≥0，0⁰＜A＜180⁰ ）  机器人在平面上能完成下列动作：先原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离S，现机器人在直角坐标系的坐标原点，且面对x轴正方向，①若给机器人下了一个指令[4，60⁰]，则机器人应移动到点________；

②请你给机器人下一个指令_________，使其移动到点（－5，5）。

三、解答题（本题有7小题，共72分）

19、（本小题8分）解方程

20、（本小题9分）先将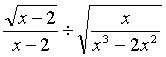化简，然后自选适合的x值，代入化简后的式子求值。

21、（本小题8分）已知关于x的函数y=(k－1)x²+2kx+k+4的图象与直线y=1有两个不同交点，求k的取值范围。

22、（本小题9分）阅读下面材料，并解答下列问题。

在形如a^b=N中，我们已经研究过两种运算：（1）已知a和b，求N，

这是乘方运算；（2）已知b和N，求a，这是开方运算：现在我们研究第三种运算：已知a和N，求b，我们把这种运算叫做对数运算。定义：若a^b=N

(a＞0,a≠1,N＞0)，则b叫做以a为底N的对数，记作.

例如：因为a³=8，所以；因为.，所以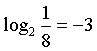

①根据定义计算：

;　;　;

如果，那么x=______.

②设a^x=M，a^y =N, 则(a＞0,a≠1,　M、N均为正数)

因为a^x ·a^y = a^x+y，所以a^x+y=M·N，所以，

即

这是对数运算的重要性质，进一步，我们可以得到：

（其中均为正数，a＞0,a≠1）

23、（本小题12分）某种产品的年产品不超过1000吨，该产品的年产量

（单位：吨）与费用（单位：万元）之间函数的图象是顶点在原点的抛

物线的一部分（如图1所示）；该产品的年销售量（单位：吨）与销售单价

（单位：万元/吨）之间函数的图象是线段（如图2所示）。若生产出的产品都能在当年销售完，问年产量是多少顿时，所获毛利润最大？（毛利润=销售额-费用）

　　..　　　　  图1　　　　　　　　　　　　　　  图2

24、（本小题12分）已知正方形的边长为1.

　 　　 

　　(a)　　　　 (b)　　　　　　 (c)　　　　　　　　　　 (d)

ⅰ、如图(a)，可计算出正方形的对角线长为_______，如图（b）两个并排放着的矩形的对角线长________，n个呢？_________-

ⅱ、若把(a),(d)两图操作拼成如下“L”形, 过C作直线交DE于A,交DF于B

①若DB=,求DA的长度

②若DA,DB是方程2x²－(2k+1)x+k²－7=0的两根, 求k的值.

25、（本小题14分）如图已知圆心A（0，3），⊙A与x轴相切，⊙B的圆心在x轴的正半轴上，且⊙B与⊙A外切于点P，两圆的公切线MP交y轴于点M，交x轴于点N.

（1）若sin∠OAB=，求直线MP的解析式及经过M、N、B三点的抛物线的解析式。

（2）若⊙A的位置大小不变，⊙B的圆心在x轴的正半轴上移动，并使⊙B与⊙A始终外切，过M作⊙B的切线MC，切点为C，在此变化过程中探究 ：①四边形OMCB是什么四边形，对你的结论加以证明。

②经过M、N、B三点上午抛物线内是否存在以BN为腰的等腰三角形？若存在，请写出另一顶点的坐标（不要求写过程）；若不存在，说明理由。

　

班级_________

姓名_________学号_________

.

初三质量调查卷答题卷

（考试时间100分钟，总分150分）

一、选择题:（本题12小题，每小题4分，共48分）

1、　　　　 2、　　　　　 3、　　　　　 4、　　　　　 5、 

6、　　　　 7、　　　　　 8、　　　　　 9、　　　　　 10、

11、　　　　　　　　　　　　　　　  12、

二、填空题:（本题6小题，每小题5分，共30分）

13、　　　　14、　　　　  15、　　　　　 16、　　　　 17、

18、　　

三、解答题：（本题7小题，共72分）

19、（本小题8分）

20、（本小题9分）

21、（本小题8分）

22、（本小题9分）

①___________,  ____________,  _____________,　_____________

②_____________________

23、（本小题12分）

24、（本小题9分）

ⅰ、_____________,  ______________,  ______________.

ⅱ、①解：

②解：　　　　　　　　　　　　　　　　　　　

25、解：