2005年中考数学模拟试卷　

（命题人：深圳市东湖中学　王义平）

（2005年4月25日）

注意事项：1、本试卷满分100分，满答案时间90分钟。2、允许使用科学计算器。

一、选择题（将下列各题中唯一正确的答案代号填在相应的答案栏内，每题3分，共计30分）

题号	1	2	3	4	5	6	7	8	9	10
答案

1.下列运算正确的是

A 、　B、　 C 、　 D、（⁰-⁰=1

2．初三年级进行了一次数学测验，参考人数共540人，为了了解这次数学测验成绩，下列所抽取的样本中较为合理的是

A．抽取前100名同学的数学成绩　　　 B．抽取后100名同学的数学成绩

C．抽取（1）、（2）两班同学的数学成绩　　 D.抽取学号是5的倍数同学的数学成绩

3、观察下列平面图形，其中轴对称图形有（　　 ）

A、1个　　　　　 B、2个　　　　　 C、3个　　　　　  D、4个

4、转动A、B两个盘当指针分别指向红色和蓝色时称为配紫色成功。如图转动A、B各一次配紫色成功的概率是

A、　　 B、　　　 C、　　　　　  D 、

5、若铺地面的瓷砖每一个顶点处都有六个相同的正多边形组成，则这种正多边形只能是（ 　）

A．正三角形　　　B．正方形　　　　 C．正五边形　　　 D．正六边形

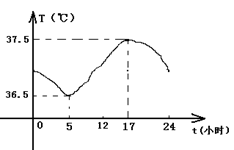6、正常人的体温一般在37℃左右，但一天中的不同时刻不尽相同.下图反映了一天24小时内小明体温的变化情况，下列说法错误的是（　　）

A．清晨5时体温最低　　　　　

B．下午5时体温最高

C．这一天中小明体温T(单位：℃)的范围是36.5≤T≤37.5

D．从5时至24时，小明体温一直是升高的.

7、在半径为8cm的圆中，垂直平分半径的弦长为(　  )。

 A．4cm　　 B．4cm　　　　C．8cm　　　　　　  D．8cm

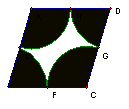
8、如图，菱形ABCD，边长等于2，点E、F、G、H分别是AB、BC、CD、DA的中点，图中阴影部分由四个小扇形组成，对于下列判断中正确的有（　 ）

1空白图形空白部分的周长=2　　2空白部分的面积=  

3四个小扇形的面积和 =　　　  4菱形的面积=4　

A 1个　B 2个　C 3个　  D 4个

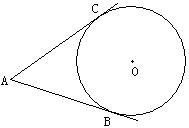9、如图AB、AC与⊙O相切于B、C，∠A=50^O，点P是圆上异于B、C的一动点，则∠BPC的度数是（　 ）

A．65^O　　　　　　 

B．115^O　　　

C．65^O 和115^O　　　

D．130^O 和50^O

10．生物学指出：在生态系统中每输入一个营养链的能量大约有的能量难够流到下一个营养级，在H₁H₂ H₃ H₄H₅H₆这条生物链中，（H_n表示第n个营养级，n=1，2，3，4，5，6）要使H₆获得10千焦的能量，需要H₁提供的能量是（　）

A 、10⁴ B 、10⁵ C 、 10⁶ D、10⁷

二、填空题（1-3小题每题2分，其余每题3分，共 18 分）

11、的相反数是　　 ；

12、如果全国每人每天节约一杯水，那么全国每天节水约32500m³ , 用科学记数法表示：　　　　 

13、∠的补角是125º，则∠=　　　　；

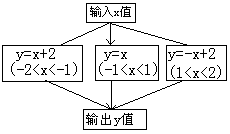14、右图的程序计算函数值，

若输入x的值为，

则输出的结果y为　　　　。

15、初三年级参加体育运动会时组成队形为10排，第一排20人，而后面每排比前排多1 人，写出每排人数m与这排数n之间的函数关系式　　　　  ，自变量的取值范围是　　　　 ；

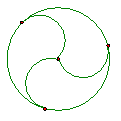
16、如图，把一个圆分成三等份，请你再设计1—2个不同的方法，把圆分成三等到份。（正确划分一个圆得2分，正确划分二个圆得3分）

17、如图，把一张矩形纸片ABCD沿BD对折，

使点C落在E处，BE与AD相交于点O，

写出一组相等的线段　　　　　  ；

（不包括AB=CD，AD=BC）

三、解答题

18（4分）、先化简下面的式子，再自取一个适当的的值代入求值

19（1小题2分，2、3小题各3分，共8分）、心理学家发现，学生对概念的接受能力y与提出概念的时间x（单位：分）之间满足函数关系：（），y越大，表示接受能力越强。

（1）第10分钟时，学生接受能力是多少？

（2）当x在什么范围内，学生接受能力逐渐增强；当x在什么范围内，学生接受能力逐渐减弱。

（3）第几分钟时，学生接受能力最强？

20（每小题4分，共8分）、某校组织师生春游，若单独租用45座的客车若干辆，则刚好坐满；若单独租用60座的客车，则可以少租一辆，且余30个空位

（1）　　求该校参加春游的人数；

（2）　　该校决定这次春游同时租用这两种车，其中60座客车比30座客车多租一辆，这样比单独租用一辆节省租金。已知45座客车每辆租金250元，60座客车每辆租金为300元请你你帮助设计本次春游所需车辆的租金。

21（第1小题4分，2-3小题各3分，共10分）、在矩形ABCD中，点EFGH分别是边ABBCCDDA的中点，顺次连结E₁F₁G₁H₁所得的四边形我们称之为中点四边形如图

（1）　　求证：四边形E₁F₁G₁H₁是菱形；

（2）设E₁F₁G₁H₁的中点四边形是　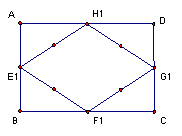　　　　　   E₂F₂G₂H₂，E₂F₂G₂H₂的中点四边形形是

E₃F₃G₃H₃….E_n-1F_n-1G_n-1H_n-1的中点四边形

是E_nF_nG_nH_n，那么这些中点四边形形状的变化有

没有规律性？　　　　　　 （填“有”或“无” ）若有，说出其中的规律性

　　　　　　　　　　　 

（3）　　进一步：如果我们规定：矩形=0，菱形=1，并将矩形ABCD的中点四边形用f(0)表示；菱形的中点四边形用f(1)表示，由题（1）知，f(0)=1，那么

么 f(1)=　　　　　

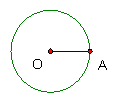
22（1、2两题各3分，3小题4分，共10分）、（1）填空：如图，我们知道，一条线段OA绕着它的一个端点O旋转一周，另一个端点所形成的图形叫做　　　 ；一个矩形ABCD绕着它的边AB旋转一周所形成的图形叫做　　　　；

　　

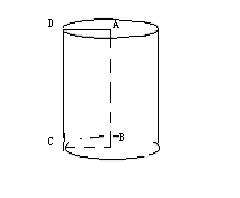
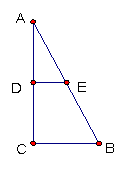
（2）如上右图，将一个直角三角形ABC（∠C=90⁰）绕着它的直角边AC旋转一周，也能形成一个几何图形。

（a）在上右图中画出这个旋转图形的草图，并说出它的名称。

（b）如果ΔABC中AC=20，BC=15，把这个旋转图形沿着ΔABC的中位线DE且垂直于AC的方向横截，得到一个什么样的图形？并请你计算所截图形的上半部分的全面积。

23、（每小题4分，共12分）已知：如图，点P是半径为5cm的⊙O外的一点，OP= 13cm，PT切⊙O于T点，过点P作⊙O的割线PAB（PB>PA），设PA= x，PB= y。

（1）求y与x的函数解析式，并确定自变量x的取值范围；

（2）这个函数有最大值吗？若有求出此时△PBT的面积，若没有，请说明理由；

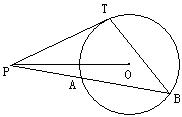（3）是否存在这样的割线PAB，使得，若存在，请求出PA的值，若不存在，请说明理由。

中考模拟题答案（王义平）

一、1、B　2、D　3、D　4、A　5、A　

6、D　7、D　8、B　 9、C　10、C

二、11 、2　12 、3.25　 13、55　 14、 0.5　15、 m=10+(n-1)　 (10n20)　16 、 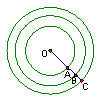 其中OA；OB：OC=1：：　　　　　　　　　　  17、OA=OE （或OB=OD或 AB=DE或 BC=BE）　　18、

19、（1）当x=10时，y=-10+26+43=59

　　(2)y=-0.1(x²-26x+13²-13²)+43=-0.1(x-13)²+59.9

　　当x<13 时,渐增强

当x>13时,渐减弱

(3)当x=13时，最强，达到59.9

20、(1) 270人　　设学生人数为x人　 方程是　  x=270

(2) 1400元.　 单独租用一种车辆，所需费用均为1500元。设租用45座的车辆为x辆，

则有方程式

　　45x+60(x+1)≥270

250x+300(x+1)≤1500　　　　　

21、（1）连结AC、BD，证E₁F₁∥G₁H₁，且₁ E₁F₁= G₁H₁，_，  E₁F₁=E₁H₁

（2）有，菱形与矩形交替出现

（3）f(1)=0

22、（1）圆，圆柱 

　 （2）（a）圆锥体

（b）150

23、（1）y=  8<x<12

(2)有最大值。当PAB与PO重合时y最大， y_最大=18,　 这时S=

（3）存在这样的割线PAB，A是PB的中点，这时，PA=x=6