市2006年初三年级调研考试
数 学 试 题
本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分130分.考试时间120分钟.
注意事项:1.答卷前,考生务必将第Ⅱ卷密封线内各项填写清楚.
2.选择题答案填在第Ⅱ卷指定的答题栏内,考试结束后考生只交第Ⅱ卷.
第I卷(选择题 共36分)
一、选择题(下列各题给出的四个选项中,只有一个是正确的.每小题3分)
1.若![]() ,则
,则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() 或—
或—![]() (D)
(D)![]() 或—
或—![]()
2.已知2是关于![]() 的方程
的方程![]() 的解,则
的解,则![]() 的值是
的值是
(A)![]() (B)
(B)![]() (C)5
(D)
(C)5
(D)![]()
3.若![]() ,则
,则![]() 的值等于
的值等于
(A)6 (B)9 (C)12 (D)81
4.下列四个函数中,自变量的取值范围为![]() ≥1的是
≥1的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等边三角形、等腰梯形、菱形、正五边形等四种方案,你认为符合条件的是
(A) 等边三角形 (B) 等腰梯形
(C) 菱形 (D) 正五边形
6. 千年飞天梦,今朝终成真.2003年10月15日是每个中国人为之骄傲的日子,我国研制的神舟五号飞船顺利发射升空,按预定轨道环绕地球24圈共飞行60多万千米后成功着陆.用科学记数法表示60万千米是
(A)![]() 千米 (B)
千米 (B) ![]() 千米 (C)
千米 (C) ![]() 千米
(D)
千米
(D) ![]() 千米
千米
7.已知一多边形的每一个内角都等于150°,则这个多边形是
(A) 十二边形 (B) 十边形 (C) 八边形 (D) 六边形
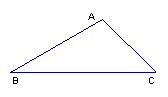 8.如图,在
8.如图,在![]() 中,
中,![]() ,
,![]() ,那么以
,那么以![]() 为圆心、6为半径的⊙
为圆心、6为半径的⊙![]() 与直线
与直线![]() 的位置关系是
的位置关系是
(A) 相交 (B) 相切
![]() (C)
相离
(D)
不能确定
(C)
相离
(D)
不能确定
9.2003年“十•一”黄金周期间,我市花果山风景区在7天假期中,共接待游客的人数(单位:万人)统计如下表:
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数 | 1.2 | 2 | 2.5 | 2 | 1.2 | 2 | 0.6 |
其中众数和中位数分别是
(A) 1.2,2 (B) 2,2.5 (C) 2,2 (D) 1.2,2.5
10.随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费按原标准降低了![]() 元后,再次下调了25%,现在的收费标准是每分钟
元后,再次下调了25%,现在的收费标准是每分钟![]() 元,则原收费标准每分钟为
元,则原收费标准每分钟为
(A) ![]() 元
(B)
元
(B) ![]() 元
(C)
元
(C) ![]() 元 (D)
元 (D)![]() 元
元
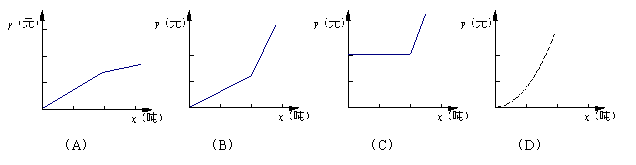
11.水是地球上极宝贵的资源.某城市为了节约用水,实行了价格调控,限定每月每户用水量不超过6吨时,每吨价格为 2.25元;当用水量超过6吨时,超过部分每吨价格为3.25元.则按此调控价格的每户每月水费![]() (元)与用水量
(元)与用水量![]() (吨)的函数图像大致为
(吨)的函数图像大致为
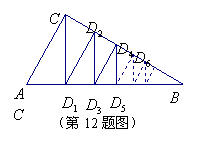 12.如图,
12.如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,这样继续作下去,……,线段
,这样继续作下去,……,线段![]() 能等于(
能等于(![]() 为正整数)
为正整数)
(A) ![]() (B)
(B) ![]()
(C)![]() (D)
(D)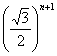
市2006年初三年级调研考试
数 学 试 题
| 题 号 | 一 | 二 | 19 | 20 | 21 | 22 | 23 | 24 | 总 分 |
| 得 分 |
|
|
|
|
|
|
|
|
|
选择题答题处
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 |
第Ⅱ卷(非选择题 共94分)
| 得分 | 评卷人 | 复评人 |
二、填空题(每小题3分,共18分.请将答案直接填在题中横线上)
 13.计算:
13.计算:![]() =
.
=
.
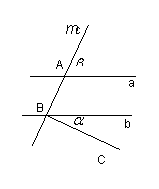
14.如图,直线![]() ∥
∥![]() ,直线
,直线![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() ,垂足为
,垂足为![]() .若
.若![]() ,则
,则![]() 为
°.
为
°.
15.方程组![]() 的解是
.
的解是
.
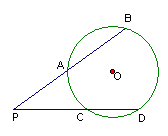
![]() 16.已知:如图,
16.已知:如图,![]() 、
、![]() 是⊙
是⊙![]() 的割线,
的割线,![]() ,
,![]() ,
,![]() .则
.则![]() =
=
![]() .
.
![]() 17.一个学生荡秋千,秋千链子的长度为
17.一个学生荡秋千,秋千链子的长度为![]() ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是
,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是![]() ,则它摆至最高位置时与其摆至最低位置时的高度之差为
,则它摆至最高位置时与其摆至最低位置时的高度之差为 ![]() .
.
(结果可以保留根号)
18.我市出租车收费标准如下:
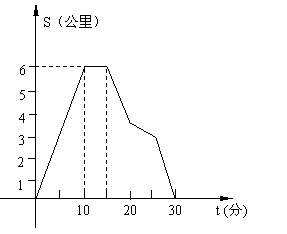 起租费:5元;基价里程:3公里;
起租费:5元;基价里程:3公里;
等时费:每等5分钟加收1公里的租价;
租 价:每公里1.20元.
星期天,某同学从家出发坐出租车去新浦
火车站接一朋友回家.如图,表示该同学离家
时间与所行路程之间的关系,则该同学最少应付车
费 元.(注:1公里=1千米)
![]()
三、解答题 (共76分.解答应写出必要的文字说明、演算步骤或证明过程)
| 得分 | 评卷人 | 复评人 |
19.(每小题满分5分,共15分)
(1)解不等式:![]() ≤
≤![]() .
.
(2)将多项式![]() 分解因式.
分解因式.
(3)已知![]() 是方程
是方程![]() 的一个根,求
的一个根,求![]() 的值和方程其余的根.
的值和方程其余的根.
| 得分 | 评卷人 | 复评人 |
20.(每小题满分6分,共24分)
(1)“三等分一个角”是数学史上一个著名问题,今天人们已经知道,仅用圆规和直尺是不可能作出的.在探索中,有人曾利用过如下的图形.
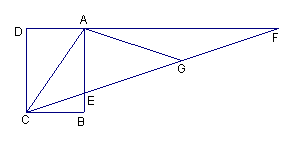 其中,四边形
其中,四边形![]() 是矩形,
是矩形,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 是
是![]() 上一点,并且
上一点,并且![]() ,你能证明
,你能证明![]() 吗?
吗?
(2)某工厂下设甲、乙两个分厂。总厂要评估各分厂的生产效率,并据此来提高职工奖金,下表给出了甲、乙两分厂的产量情况.
| 甲 厂 | 乙 厂 | |||
| 产量(只) | 工人数(人) | 产量(只) | 工人数 | |
| 新车间 | 700000 | 140 | 600000 | 100 |
| 老车间 | 120000 | 60 | 210000 | 100 |
甲厂的负责人说:我工厂人数与乙厂相同,总产量比乙厂高,应该率先提高工人奖金,你同意他的说法吗?为什么?
(3)已知关于x的方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() .
.
① 求k的取值范围;
② 是否存在实数k,使方程的两实数根互为相反数?如果存在,求出k的值;如果不存在,请说明理由.
解:①根据题意,得 Δ=![]() ,
,
又∵方程有两个不相等的实数根,∴Δ>0,即![]() >0,解得
k<
>0,解得
k<![]() 。
。
∴ k的取值范围为k<![]() .
.
② 存在. 如果方程的两实数根![]() 互为相反数,则
互为相反数,则
![]() ,
,
又 ![]() ,∴
,∴![]() ……………………(﹡)
……………………(﹡)
解得 ![]() . 经检验
. 经检验![]() 是方程(﹡)的解.
是方程(﹡)的解.
∴当![]() 时,方程的两实数根
时,方程的两实数根![]() 互为相反数.
互为相反数.
读了上面的解答过程,请判断是否有错误?如果有,请指出错误之处,并直接写出正确答案.
| 座位号 |
(4)如图(天平均处于平衡状态),共有四种物品:烧杯、烧瓶、量筒、砝码.仔细观察并算一算几个烧杯才能跟一个烧瓶平衡?

| 得分 | 评卷人 | 复评人 |
21.(本题满分7分)
某手机生产厂家根据其产品在市场上的销售情况,决定对原来以每部2000元出售的一款彩屏手机进行调价,并按新单价的八折优惠出售,结果每部手机仍可获得实际销售价的20%的利润(利润=销售价—成本价).已知该款手机每部成本价是原销售单价的60%.
(1)求调整后这款彩屏手机的新单价是每部多少元?让利后的实际销售价是每部多少元?
(2)为使今年按新单价让利销售的利润不低于20万元,今年至少应销售这款彩屏手机多少部?
| 得分 | 评卷人 | 复评人 |
22.(本题满分8分)
(1)如图,是边长为1的![]() (
(![]() 为大于1的整数)个连续小正方形所组成的图形.
为大于1的整数)个连续小正方形所组成的图形.
……
4个小正方形 9个小正方形
它们经过适当分割(指只用剪刀沿直线剪开,不借助于其它任何工具)后都能拼成一个大正方形,其分割线(图中实线)的最少条数与小正方形的个数之间关系见下表,请填写下表中的空白处:
| 小正方形的个数 | 4 | 9 | 16 | … |
|
| 分割线的最少条数 | 1 | 2 | … |

![]() (2)如图,边长为1的5个连续小正方形所组成的图形按(1)中的要求经过4次分割后也能拼成一个大正方形,其拼成后的图形见方格纸。
(2)如图,边长为1的5个连续小正方形所组成的图形按(1)中的要求经过4次分割后也能拼成一个大正方形,其拼成后的图形见方格纸。
5个小正方形 10个小正方形
边长为1的10个连续小正方形组成的图形,是否
也能够按(1)中的要求经过适当分割后拼成一个大正
方形呢?如果能,则分割线的最少条数为 条。
请在上图中画出分割线,并将分割后拼成的大正方形
画在方格纸中。
(3)你是否还能举出一种非![]() (
(![]() 为大于1的整数)个
为大于1的整数)个
连续小正方形所组成的图形,按(1)中的要求经过适当
分割后能拼成一个大正方形呢?试试看!
连续小正方形的个数为 个,分割线的最少条数为 条。
| 得分 | 评卷人 | 复评人 |
23.(本题满分10分)
行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑动一段距离才停止,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过130km/h),对这种汽车进行测试,测得数据如下表:
| 刹车时车速(km/h) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| 刹车距离(m) | 0 | 1.1 | 2.4 | 3.9 | 5.6 | 7.5 | 9.6 | 11.9 |
(1)以车速为x轴,刹车距离为y轴,在下面的方格图中建立坐标系,描出这些数据所表示的点,并用平滑曲线联接这些点,得到函数的大致图像.
(2)观察图像,估计该函数的类型,并确定一个满足这些数据的函数解析式;
(3)该型号汽车在国道上发生了一次交通事故,现测得刹车距离为26.4m.问在事故发生时,汽车是超速行驶还是正常行驶?请说明理由.
| 得分 | 评卷人 | 复评人 |
24.(本题满分12分)
在![]() 中,
中,![]() ,
,![]() .以
.以![]() 上的点
上的点![]() 为圆心、
为圆心、![]() 为半径的圆与
为半径的圆与![]() 相切于点
相切于点![]() ,交
,交![]() 于
于![]() .过点
.过点![]() 作⊙
作⊙![]() 的切线,切点为
的切线,切点为![]() .过点
.过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交⊙
,交⊙![]() 于
于![]() ,
,
(1)求证:四边形![]() 是正方形;
是正方形;
(2)求⊙![]() 的半径;
的半径;
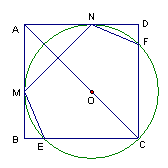 (3)连结
(3)连结![]() 、
、![]() 、
、![]() ,在五边形
,在五边形![]() 的5条边中,若从相等关系考虑,你能得到哪些结论?请给出证明.
的5条边中,若从相等关系考虑,你能得到哪些结论?请给出证明.
|
市2006年初三年级调研考试数学试题
参考答案及评分标准
一、选择题:![]()
![]()
二、填空题:
13、![]() ;14、65;15、
;14、65;15、
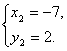 16、8;17、
16、8;17、![]() ;18、17.
;18、17.
三、解答题:
19.(1)![]() ≥-2; (2)
≥-2; (2)![]() ; (3)
; (3)![]() (2分),另一根是2.(3分)
(2分),另一根是2.(3分)
20.(1)证明:∵![]() ,又∵
,又∵ ![]() ,
,
∴![]() . ………………………………………………3分
. ………………………………………………3分
∵ ![]() ∥
∥![]() ,∴
,∴![]() , ………………………………1分
, ………………………………1分
∴![]() , ∴
, ∴ ![]() . ……………………2分
. ……………………2分
(2)同意. ∵甲厂的总生产效率为:![]() =4100(只/人);
=4100(只/人);
乙厂的总生产效率为:![]() =4050(只/人).
=4050(只/人).
∴甲厂的总生产效率高于乙厂的总生产效率. ……………………4分
故 应先提高甲厂的工人奖金. ………………………………………2分
[或不同意.∵甲厂的新车间生产效率为:![]() =5000(只/人);
=5000(只/人);
甲厂的老车间生产效率为:![]() =2000(只/人).
=2000(只/人).
而 乙厂的新车间生产效率为:![]() =6000(只/人);
=6000(只/人);
乙厂的老车间生产效率为:![]() =2100(只/人). ……4分
=2100(只/人). ……4分
∴ 乙厂的新老车间的生产效率分别比较甲厂新老车间的生产效率高,
故 不应先提高甲厂的工人奖金. …………………………………2分]
(3)有错误.①没有考虑二次项的系数不为零.…………………………………………1分
正确答案应为:![]() 的取值范围是
的取值范围是![]() <
<![]() 且
且![]() ≠0. ………………………2分
≠0. ………………………2分
②![]() 不在其取值范围内,应舍去.…… ……………………………1分
不在其取值范围内,应舍去.…… ……………………………1分
正确答案应为:不存在实数![]() ,使方程的两实数根
,使方程的两实数根![]() 互为相反数. 2分
互为相反数. 2分
(4)解:设一个烧瓶重![]() 克,一个烧杯重
克,一个烧杯重![]() 克,一个量筒重
克,一个量筒重![]() 克,一个砝码重
克,一个砝码重![]() 克.
克.
|
|
|
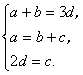 ……………………………………3分
……………………………………3分
将③代入②,得 ![]() .
④
…………………………………1分
.
④
…………………………………1分
由①④,得 ![]() . …………………………………………………1分
. …………………………………………………1分
故 5个烧杯才能跟一个烧瓶平衡. ……………………………………1分
21.解:(1)由题意,知 成本价为:![]() %=1200(元). ……………………1分
%=1200(元). ……………………1分
设这款彩屏手机的新单价为每部![]() 元.根据题意,得
元.根据题意,得
1200+20%•80%![]() =80%
=80%![]() ,
,
解得 ![]() . 故 新单价为每部1875元 …………………2分
. 故 新单价为每部1875元 …………………2分
所以,让利后的实际销售价每部为:1875![]() 80%=1500(元). ………1分
80%=1500(元). ………1分
(2)由题意,得 ![]() ≥200000, …………………………………1分
≥200000, …………………………………1分
解得 ![]() ≥
≥![]() . …………………………………………………………1分
. …………………………………………………………1分
 因此,今年至少应销售这款彩屏手机667部,才能使按新单价让利销售的利润不低于20万元. ……………………………………………………………………1分
因此,今年至少应销售这款彩屏手机667部,才能使按新单价让利销售的利润不低于20万元. ……………………………………………………………………1分
22.(1)3,![]() ; ……………2分
; ……………2分
 (2)5条(1分);分割线如图(1分);
(2)5条(1分);分割线如图(1分);
拼成后的大正方形见方格纸(2分).
(3)答案不惟一,只要符合下述规律即可:
连续小正方形的个数为(![]() )个,分割线的最少条数为(
)个,分割线的最少条数为(![]() )条.
)条.
如:17个,6条;26个,7条等.
23.解:(1)图略.…………………………2分
(2)该函数的图像是抛物线的一部分1分
设所求抛物线的解析式为![]() .
.
将点(0,0)、(10,1.1)、(20,2.4)代入解析式,得
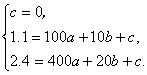 ……2分
解得
……2分
解得 ![]()
故 所求的函数解析式为 ![]() . ……………………………………2分
. ……………………………………2分
(3)当![]() 时,有
时,有 ![]() ,…………………………………1分
,…………………………………1分
解得 ![]() ,
,![]() (舍去). ……………………………………………1分
(舍去). ……………………………………………1分
∴ 刹车时的速度为![]() ,低于
,低于![]() ,故在发生事故时汽车属正常行驶. ……1分
,故在发生事故时汽车属正常行驶. ……1分
24、(1)∵![]() , ∴
, ∴ ![]() .
.
∵![]() 、
、![]() 是⊙
是⊙![]() 的切线,∴
的切线,∴![]() .∴
.∴ ![]() . ………1分
. ………1分
∵![]() ,∴
,∴![]() ,∴ 四边形
,∴ 四边形![]() 是正方形. ……………………1分
是正方形. ……………………1分
(2)设⊙![]() 的半径为
的半径为![]() . ∵
. ∵![]() ,∴
,∴![]() . …………………
…………1分
. …………………
…………1分
连结![]() ,则
,则![]() 是等腰直角三角形, ∴
是等腰直角三角形, ∴![]() ,∴
,∴![]() ,
,
∴ ![]() .…………………………………………………………………………2分
.…………………………………………………………………………2分
(或根据平行线分线段成比例定理,列出比例式计算也可)
(3)结论有:①![]() ;②
;②![]() . ………………………………………1分
. ………………………………………1分
由(2)可得,![]() ,∴
,∴ ![]() .
.
由切割线定理,得 ![]() ,∴
,∴![]() ,∴
,∴![]() .
.
同理可得 ![]() , ∴
, ∴ ![]() ,∴
,∴![]() . ………………2分
. ………………2分
又 ![]() ,
,
而 ![]() , ∴
, ∴![]() . …………………2分
. …………………2分
(或根据对称性质找出相等线段,只要说理正确也可参照评分)
(注:每题中若有其他证法或解法,只要正确,请参照本评分标准进行评分)