初三中考数学模拟考试
一、选择题：（本题共5小题，每小题3分，共15分）
1、5的相反数是（ ）
A 
B 
C 5 D 
2、下列各式运算正确的是（ ）
A 
B 
C 
D 
3、已知圆
的半径为2。圆
的半径为3，两圆的圆心距为5，则两圆的位
置关系是（ ）
A 相交 B 相离 C 外切 D 内切
4、圆锥底面的半径为5cm，高为12cm,则该圆柱的侧面积为（ ）
A 60
B 
C 
D 
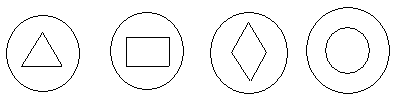
5、如图（1），将一圆形纸片对折两次，然后沿着图中的虚线剪开，得到两部分，
其中一部分展开后的平面图形是（ ）
|
二、填空题：（本题共5小题，每小题4分，共20分）
6、长江三峡工程电站的总装机容量是18，200，000千瓦，用科学记数法表示
电站的总装机容量，应记为 千瓦。
7、方程: 
的解是
|
垂足分别是D，E，
BE，CD交于点O，且AO平分
|
|
|
9、分解因式：
。
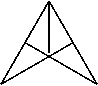
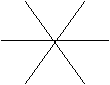
10、如图在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为
2，则图中阴影部分的面积为
。
|  | ||
11、化简求值：
其中
.
12、等腰梯形ABCD中，
，E，F分别在
AD，CD上，DE=CF，AF，BE交于点P，请你量一量
的度数，
并证明你的结论。
13、解方程组
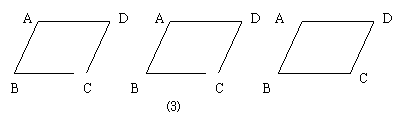
14、在一次数学探究活动中，小强用两条直线把平行四边形ABCD分割成
四部分，使含有一组对顶角的两个图形全等。
⑴根据小强的分割方法，你认为平行四边形割成满足以上全等关系的直线
有 组；
⑵请在图⑶的三个平行四边形中画出满足小强分割方法的直线；
⑶由上述实验操作过程中，你发现所画的两条直线有什么规律？
 |
15、为了了解某初中学生的体能情况，抽取若干名学生在
单位时间内进行引体向上，将所得数据整理后画出频率分
布直方图，（如图）图中从左到右依次是1、2、3、4、5组
|
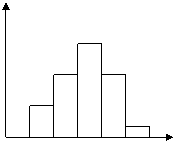①、求抽取多少名学生参加测试
|
③若次数在5次（含5次）以上为达标，
|
求这次测试的达标率。
 |
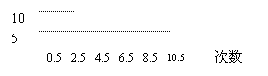四、解答题：（本题共4小题，每小题7分，共28分）
16、某地举行乒乓球比赛的费用y(元)包括两部分：一部分是租用
比赛场地等固定不变的费用b（元），另一部分与比赛的人数x（人）
成正比例。当x=20时,y=1600，当x=30时，y=2000,
①求y与x之间的函数关系式；
②如果有50名运动员参加比赛，且全部费用由运动员分摊，
那么每名运动员需支付多少元？
17、四月份以来，我省普降大雨，造成多处受灾，为了加强防汛工
作，市工程队准备对一段长为2240米的河堤进行加固，由于采用新
的加固模式，现在计划每天加固的长度比原计划增加了20米，因而完
成此段加固工程所需天数将比原计划缩短2天，为进一步缩短该段加
固工程的时间，如果要求每天加固224米，那么在现在计划的基础上，
每天加固的长度还要再增加多少米？
 |
18、已知抛物线
经过点A(
),B
,C
三点，
①求抛物线的解析式；②若抛物线的顶点为D，求
的值。
19、如图，在四边形ABCD中，对角线
，垂足为P
求证：
。
证明:
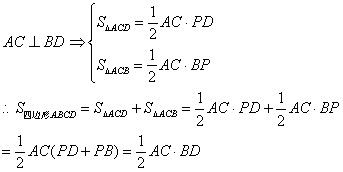
解答问题：①、上述证明得到的性质可叙述为
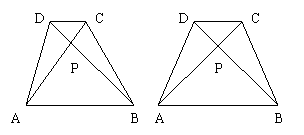
②已知:等腰梯形ABCD中,
且交于点P,
AD=3cm,BC=7cm,利用上述性质求梯形面积.
 |
20、如图所示：A，B为两个村庄，AB，BC，CD为公路，BD为田地，AD
为河宽，且CD与AD互相垂直，现在要从点E处开始铺设通往村庄A，村
庄B的一条电缆，共有两种铺设方案：
方案一：
方案二：
；
经测量得
|
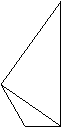①求出河宽（结果保留根号）
|
③哪种铺设电缆的费用低？请说明你的理由？
| |||
 | |||
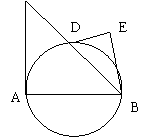
21、已知：AB是圆O的直径，AC切圆O于A，CB交于D，DE切圆O于D，
，垂足是E，BD=10，DE，BE 是方程
|
22:菱形ABCD的边长为6cm,
,点M是边AD上的一点,且DM=2cm,
点E,F分别从A,C同时出发,以1cm/s的速度分别沿边AB,CB向点B运动,EM,CD
的延长线相交于G,GF交AD于O,设运动时间为x(s)
的面积为y
①求y与x之间的函数关系式；
②当x为何值时,
③是否存在某一时刻,使得线段GF把菱形ABCD分成上下两部分的面积之比为3:7?若存在,
求出此时x的值;若不存在,请说明理由.
 |