初三数学期末考试卷

题号	一	二	三	四	五	总分
得分

说明：全卷8页，考试时间为90分钟，满分120分。

一、选择题：（本题共5小题，每小题3分，共15分。每小题给出的4个选项中只有一个是正确的，请把所选选项的字母写在题后的括号内）

1、在△ABC中，△∠C=90°，BC=5，AB=13，则sinA的值是（　 ）

　　A、　　  B、　　  C、　　 D、

2、在平面直角坐标系中，点P（－1，1）关于X轴的对称点在（　 ）

　　A、第一象限　　　B、第二象限　　　C、第三象限　　 D、第四象限

3、已知两圆有4条公切线，则这两圆的位置关系是（　　）

　 A、相交　　 B、外切　　C、内切　　D、外离

4、函数y=ax²与y=ax+b (a>0, b>0)在同一坐标系中的大致图象是（　 ）

 

5、函数y=的自变量x的取值范围是（　　）

　　A、x≥－2　　 B、x<－2　　C、x >2　　　D、x≤－2

二、填空题（本题共5小题，每小题4分，共20分.）

6、如图：⊙O中，∠AOB=100°，则∠ACB=____________

7、一元二次方程x²－2x－1=0的两根为x₁、x₂，那么　 +=________________.

8、计算：sin45°－sin30°cos60°－tg45°=____________.

9、若反比例函数y= 图象经过点A（2，－1），则K=__________。

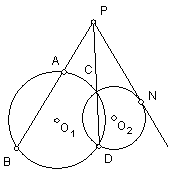10、如图，⊙O₁与⊙O₂相交于C、D两点，⊙O₁的割线

PAB与DC的延长线交于点P，PN与⊙O₂相切于点

N，若PB=10,AB=6,则PN=__________。

三、解答题（本题共5小题，每小题6分，共30分。）

11、解方程：x²+x－+1=0

12、如图，直线AB交⊙O于C、D且AC=BD，连结OA、OB，求证：OA=OB。

13、尺规作图：（保留作图痕迹，不写作法）（6分）

已知：弧AB

求作：弧AB的中点

14、直线Y=KX+b经过点P（0，－12），且与X轴、Y轴所围成的三角形面积为24，求它的解析式。

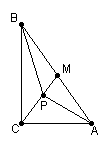
15、已知：△ABC中，∠C=90°，AC=15，BC=20，M为AB中点，P为CM上任一点（点P与C、M不重合）CP=X,试写出△PAB的面积Y与X的函数关系式。

四、解答题（本题共4小题，每小题7分，共28分。）

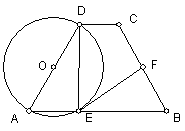
16、如图，梯形ABCD中，AB∥DC, AD=BC, 以AD为直径的⊙O交AB于E，⊙O的

切线EF交BC于F。求证：BF·BC=BE·AE。

17、如图，割线PBC经过⊙O的圆心O点交⊙O于B，C，A是⊙O上一点，AD⊥BC

于D，若AB平分∠PAD。求证：PA是⊙O的切线。

18、如图，AB是⊙O直径，BC是切线，E是BC上一点。若∠C=45°，

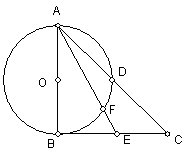求证：CD·CA=AF·AE

19、已知二次函数的图象过A（0，1），B（1，3），C（-1，1）三点，确定二次函数的解析式及顶点坐标与对称轴。

五、解答题（每小题9分，共27分）

20、如图，AB是⊙O的直径，AC是弦，D为劣弧AC上一点，弦DE⊥AB于点H，交AC于点F。

1） 若P为ED的延长线上一点，当PC=PF时，求证：PC是⊙O的切线；

2） 当C点在何位置时，若D是劣弧AC的中点，能否使AO²=DE·AF成立？写出你的猜想，并加以证明。

21、已知：如图，直线AB切⊙O于点A，CD是⊙O的直径，DB⊥AB于B点。若AB=4，BD=3.

1） 求证：DA平分∠BDC；

2） 求⊙O的直径。

22、如图，已知二次函数y₁ = 2x²- 3mx + m –1的图像过点O（0，0），与一次函数

y₂ = -x + m + 3图像交于A、B两点。

1)求二次函数与一次函数的解析式；

2）如果二次函数的图像过点P（a + 1,2b² + b - 1）,且a≠b，求a+b的值 ；

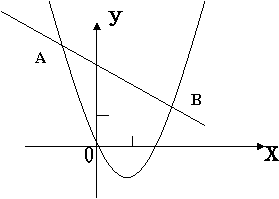
3） 利用图像求出能使y₂> y₁成立的x的取值范围。

答案

一、ACDCA

二、6、130° 7、-4　8、-　9、-2　10、2

三、11、 x₁=-2 x₂=1　　12、提示：过O作OE⊥AB于E　 13、略

14、∵y=kx+b过点P（0，12） ∴b=-12　 当y=0时，x=

　∵直线与x轴所围成的三角形的面积为24

∴ ∴k=±3

∴它的解析式为：y=3x-12或y=-3x-12

 15、解：在Rt△ABC中，　AB==25 ∴CM=AB=12.5

∵PC=x　∴PM=12.5-x 过点C作CE⊥AB，过P作PF⊥AB

∴CE=　∵△MPE∽△MCE　∴

∴PF=·CE==12-　∴y=AB·PF==150-12x

四、16、提示：证△ADE∽△BEF　　 17、提示：连结AC、AO证OA⊥PA

18、连结BF 证△AFB∽△ABE再证AB=BC

19、二次函数的解析式为：y=x²+x+1　　 顶点坐标为：（-1/2,3/4）　　对称轴是：x=-1/2

五、20、1）提示：连结OC 证∠OCP=90°

　　　　2）∵D是弧AC的中点　∴弧AD=弧DC　　∴∠AED=∠DAC　　∵∠ADE=∠FDA

　　　　∴△ADE∽△FDA　　　∴　　 ∴AD²=DE·AF

∴当∠AOD=60°时，AO²=DE·AF　 即弧AD=弧AB

∴C点为弧AB的三等分点时，AO²=DE·AF

　21、1）提示：连结AC证∠BDA=∠ADC

2)在Rt△ABD中　　AD=

由1）知∠BDA=∠ADC，∠BDA=∠ADC ∴△ACD∽△BAD　

∴　　∴

　22、1) y₁ = 2x²-3x　　 y₂ = -x + 4　　　2）a + b=-

3）依题意得：2x²-3x=-x+4　化简得：x²-x-2=0　　∴x₁=2　x₂=-1

∴由图像可知：当-1<x<2时，y₂>y₁