初（三）上数学考试试卷
A卷
一、填空题：（每题3分，共24分）
1、设路程为s（千米），速度为v（千米/小时），时间为（t小时），关系式t=50/v中，变量是 ，常量是 。
2、在几何图形中， 既是轴对称又是中心对称图。（只填写满足条件的图形一个）。
3、函数y=2x－5，当x=2时，函数值是 。
4、圆内接四边形ABCD中，如果∠B=60°，那么∠D= 度。
5、函数y=3x－2，y随x的 而增大。
6、⊙O中弦AB=8cm，弦心距为3cm，那么⊙O的半径为 ㎝。
7、用反证法证“垂直于同一条直线的两条直线平行”的第一步是 。
8、某种储蓄的月利率是0.2%，存入100元本金，本息和y（元）与所存月数x之间的函数关系式为 ，若获利不少于8元，至少应存 个月。
二、选择题：（每题3分，共15分）
9、在直角坐标系中（0，5）在（ ）
A、x轴上 B、y轴上 C、 第一象限 D、 第四象限
10、函数y=
中自变量的取值范围是（
）
A、x≥2 B、x≤2 C、x≠2 D、x>2
11、点P（2，3）关于y轴对称的点的坐标是（ ）
A、（2，－3） B、（－2，3） C、（－2，－3） D、（2，3）
12、下列各式中错误的是（ ）
A、sin30°=cos60° B、sin45°=cos45° C、cos25°=sin65° D、cos25°=sin25°
13、一次函数y=6x+8的图象经过（ ）
A、一、三、四象限 B、二、三、四象限 C、一、二、三、象限 D、一、二、四象限
三、（共20分，每小题5分）
14、用公式法解方程：x2+x－1=0 15、用配方法解方程：x2－6x+4=0
16、解方程：
17、已知一次函数y=kx+3，当x=5时，y=8，（1）求这个一次函数的解析式；（2）求这个一次函数的图象与x轴交点坐标。
四、（共12分，每小题6分）
18、解方程组：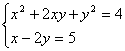
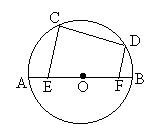19、已知：如图，AB是⊙O的直径，CD是⊙O的弦，CE⊥CD交AB于点E，DF⊥CD交AB于点F，垂足分别为C、D。求证：AE=BF。
五、（共21分，每小题7分）
20、如图，飞机于空中A处探测到地面目标C，此时飞行高度AC=1300米，从飞机上看地平面控制点B的俯角α=17°，求飞机A到控制点B的距离（精确到0.1米：参考数据
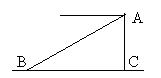sin17°=0.29，cos17°=0.96，tan17°=0.31，cot17°=3.30）
21、某厂生产一批产品，今年一月份的产量是500件，现在按合同要求在3月份的产量为720件，如果2、3两个月的平均增长率都为10%，3月份的产量能否达到720件？如果不能，那么2、3两个月的平均增长率应为多少？如果能，用代数方法说明理由。
22、关于x的方程a(1+x2)+2bx－c(1－x2)=0有两个相等的实数根，a、b、c分别为△ABC中∠A、∠B、∠C的对边，且sinB=
/2，试判断△ABC的形状。
六、（8分）
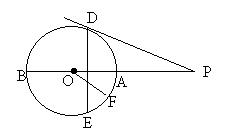23、已知：如图AB是⊙O的直径，弦DE⊥AB，垂足为C，过点D作⊙O的切线交BA的延长线于点P，tan∠P=
/15，PO=16。（1）求⊙O的半径；（2）求OC的长；（3）如果F为弧AE的中点，求cos∠AOF的值。
B卷
一、（7分）
1、已知x1、x2是方程2x2+4x－3=0的两个实数根，不解方程，求下列代数式的值：
（1）
（2）
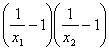
二、（8分）解方程：
三、（8分）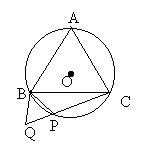
已知：如图，△ABC是⊙O的内接等边三角形，点P在弧BC上，延长CP到Q，使PQ=PB；求证：（1）△PBQ是等边三角形；（2）CQ=AP。
四：（8分）已知y－2与x+a（其中a为常数）成正比例关系，且图像过点A（0，4）、
B（－1，2），求y与x的函数关系式。
五、（9分）某校初三（3）班共有48人，有一次全班组织到水上公园进行划船活动，每只小船坐3人，租金5元，每只大船坐5人，租金8元，现租用大船x只，小船y只，如果每船要求坐满人；（1）求y与x的函数关系式，并写出自变量x的取值范围；（2）设总租金为w元，写出w关于x的函数关系式，并求最少租金是多少元？
六、（10分）已知：如图，在Rt△ABC中，∠C=90°，以AC为直径的圆O交斜边AB于点E，OD∥AB交BC于点D。（1）求证：ED是⊙O的切线；（2）求证：OC·EB=CD·CE；
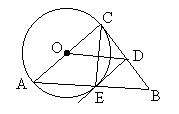（3）求证：2DE2=BE·OD。