几何综合复习（一）03.5.3
一、 三角形 四边形 相似形
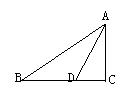
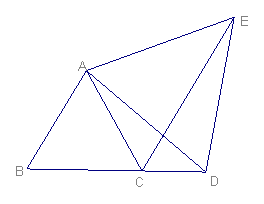1、如图，D为BC延长线上一点，△ABC、△ADE均为等边三角形，猜想EC与AB的位置关系，并证明你的猜想。
2、梯形上、下底分别为1和4，两条对角线的长分别为3和4，则梯形面积为_________。
3、矩形一边为6 cm，两条对角线交角为600，则对角线长为____________。
4、在长为1.6m，宽为1.2m的矩形铝板上，剪切如图所示的直角梯形零件（尺寸单位为mm）。这块铝板最多能剪出 个这样的零件。
5、如图：若四边形CDEF旋转后能与正方形ABCD重合，那么图形所在平面上可以作为旋转中心的点有（ ）
A、2个 B、3个 C、4个 D、5个
6、如果一个梯形的上底长是4，下底长是6，那么这个梯形被中位线分成的两部分面积之比为 （ ）
A、4∶6 B、5∶6 C、9∶10 D、9∶11
7、已知四边形ABCD的对角线AC与BD相交于O，若SΔAOB=4，SΔCOD=9。则四边形ABCD的面积的最小值是 （ ）
A、21 B、25 C、26 D、36
8、△ABC中，E在AB上，D在AC上，且AD=DC，AE∶EB=1∶2，则△AED的面积与四边形BCDE的面积的比值等于 ( )
(A)、1: 4 (B)、 1: 5 (C)、1: 6 (D)、1: 7
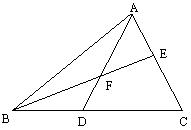
9、如图，AE:EC=1: 2，BF=FE，AF交BC于D，则BD: DC=_______。
 |  | ||
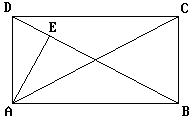10、如图，从矩形ABCD的顶点A向对角线BD引垂线AE，垂足E把BD分成两段，DE:EB=1: 3，且AD=4，则AC=_________。
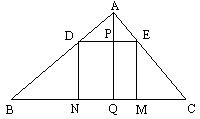11、如图，正方形DEMN内接于△ABC，AQ⊥BC于Q交DE于P，若BC=120，AQ=8，则正方形边长为_________。
12、如图，四边形ABCD、DEBF都是矩形，AB＝BF，AD、BE相交于M，BC、DF相交于N。求证：四边形BMDN是菱形。
13、如图，点M是矩形ABCD的边AD的中点，点P是BC边上一动点，PE⊥MC，PF⊥BM，垂足为E、F。
（1）当矩形ABCD的长与宽满足什么条件时，四边形PEMF为矩形？猜想并证明你的结论。
（2）在（1）中，当点P运动到什么位置时，矩形PEMF变为正方形，为什么？
二、 解直角三角形
1、在
ABC中，
=
，AC=3BC，那么cosB= ，tanA= 。
2、在ABC中，=，BC= a，
，则高AD等于 （
）
A．
B．
C．
D．
3、当
为锐角，且sinA的值大于
时，的度数 （ ）
A．小于
B. 大于 C. 小于
D. 大于
4、在ABC中，=,且
则下列关系式中，不正确的式子是( )
A．sinA=cosB B.
C.tan
= 1
D. cotA=cotB
5、在ΔABC中，∠C=90°，∠A的平分线交BC于D，则
（ ）
（A）sinA （B）cosA
（C）tgA （D）ctgA
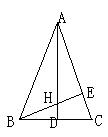6、如图，ΔABC中，AB=AC，高AD、BE相交于点H，AH=8，DH=1，求tanC
7、如图，抛物线
与
轴交点为A 、B（A在B左侧），与
轴交点为C ，顶点为P，连结PC并延长交轴于点N。
（1） 求经过P、C两点的直线解式。
（2） 
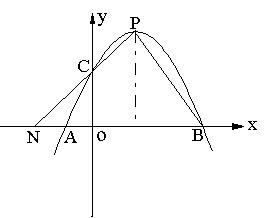求ΔNPB的面积。
（3） 求Sin∠BPN的值。
三、 圆 （直线和圆）
选择题
1、直线和圆相交，圆的半径为R，直线到圆心的距离为5，则( )
(A) R＞5 (B) R＜5 (C) R=5 (D) R≥5
2、下列判断正确的是( )
(A) 经过圆心且垂直于切线的直线必经过切点
(B) 过半径外端的直线和圆相切
(C) 和圆只有一个公共点的线段叫圆的切线
(D) 垂直于圆的半径的直线和圆相切
3、若四边形ABCD是圆的外切四边形，则下列各式中正确的是( )
(A) AB+BC=AD+DC (B) AB+CD=BC+DA
|
|
(C) ∠A+∠B=180° (D) ∠A+∠C=180°
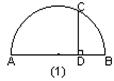
4、如图(1)：弧ACB是一个半圆，CD⊥AB于点D，若AD=4，BD=2，则CD的长是( )
(A) 2 (B)2
|
|
(C) (D)4
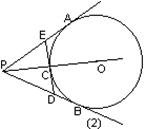
5、如图(2)：PA、PB、DE分别切⊙O于A、B、C，
如果⊙O的半径是6cm，PO长为10cm，
那么△PDE的周长是 ( )cm
(A) 16cm (B)14cm
(C) 12cm (D)10cm
|
|
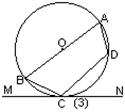
6、如图(3)：四边形ABCD为圆内接四边形，AB为直径，MN切⊙O于C点，∠BCM=38°则∠ABC=( )
(A) 38° (B) 52°
(C) 68° (D) 42°
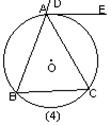
7、如图(4)：过等腰△ABC的顶点A作这个三角形外接圆的切线AE，则∠DAE与∠ABC的大小关系为 ( )
|
|
(A) ∠DAE＞∠ACB (B) ∠DAE=∠ACB
(C) ∠DAE＜∠ACB (D) 无法确定
8、若PT是⊙O的切线，T是切点，PAB是割线，交⊙O于A、B，且过O点，若∠OPT=30°，PT=10cm，则PB长为( )
(A) cm (B) cm
(C) cm (D) 10cm
|
|
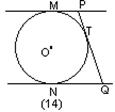
9、如图(14)，MP和NQ是半径为r的圆的两条平行切线，M、N是切点，PTQ是第三条切线，T是切点，若MP=4，NQ=9，则r=( )
(A) 12 (B) 6
(C) (D) 无法确定
|
|
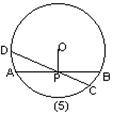
10、如图(5)，⊙O的半径为6cm，弦心距OP为4cm，AB分弦CD为2∶3，则弦CD的长为( )cm
(A) 8 (B)
(C) (D)
解答题
|
|
1、如图，已知：DP为⊙O的直径，以P为圆心作一个圆，⊙O的弦BA所在直线与⊙P切于点C
求证：PAŸPB=PCŸPD
|
|
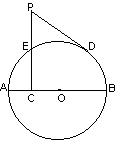
2、已知：C是⊙O的直径AB上一点，PC⊥AB与⊙O相交于E，PD是⊙O的切线，D是切点
求证：PC2=PD2+ACŸCB
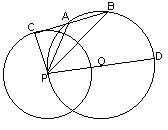
3、如图，CD是⊙O的直径，E为⊙O中半圆一动点，过E点的⊙O的切线交CD的延长线于点A，过C点的⊙O的切线交AB于点B，直线OB交⊙O于点F、G。
①求证：DE∥BG；②若AE＝4，AD＝2，求tg∠AED的值；
③若GD的延长线与AB垂直，且⊙O的半径为3，求四边形BEDG的面积。
 |
4、已知，AB是⊙O的直径，BC是⊙O的弦，⊙O的割线PDE垂直于AB于点F，交BC于点G，∠A=∠BCP.
（1） 求证：PC是⊙O的切线；
（2） 若点C在劣弧AD上运动，其条件不变，问应再具备什么条件可使结论BG2=BF·BO成立，（要求画出示意图并说明理由）.
