初三数学半期考试卷

考试座位号□□成绩　　　　 

一、填空：（每题3分，共45分）

1．  点P（3，－5）关于x轴对称的点的坐标是　　　　　　

2．  函数的自变量x的取值范围是　　　　　　　 

3．  等腰三角形的顶角的度数y与底角的度数x的函数关系式是　　　　　　　　  。

4．  若y与x成正比例关系，如果x=2时，y=4，则x=－2时，y=　　　　　　 

5．  函数y=3x－2，y随x的增大而　　　　　　 。

6．  抛物线的对称轴是　　　　　　　  。

7．  函数的图象在第　　　 象限内，在每一个象限内，y随x的增大而　　  。

8．  半径为5cm的⊙O中，有长5cm的弦AB，则圆心O到AB的距离=　　　　 。

已知：如图，AB、CD是⊙O的两条弦，OE、OF为 AB、CD的弦心距，根据圆心角、弧、弦、弦心距的 关系填空。 如果OE=OF，则　　 =　　　，　　 =　　　 ， 　　=　　　　。

9．  如图，A、B、C、D四点在⊙O上，∠ACB=140°，则∠AOB=　　　　°。

10．　　　　　　  如图，O是圆心，CP⊥AB，AP=4厘米，PD=2厘米，则OP=　　　　  。

11．　　　　　　  已知：如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于点D、E，交AB于C。写出图中所有的垂直关系　　　　　　　　　　　　　　　　　　  。

　　　 

	（第9题）		（第10题）		（第11题）

12．　　　　　　  半径分别为4厘米和1厘米的相外切的两圆的外公切线长是　　　　　 厘米。

13．　　　　　　  半径为R的圆内接正六边形的中心角的度数是　　　　  ，周长是　　  ，

有　　　　 条对称轴。

14．　　　　　　  两圆内切时，圆心距为4cm，其中一个圆半径为6cm,则另一个圆半径为　　　 。

15．　　　　　　  观察下面一列数的规律并填空，

1，4，7，10，13，………。则它的第2002个数是　　　　　　  。

二、选择：（每题3分共15分）

16．下列直线不经过第三象限的是（　　　 ）

A． y=3－4x, 　 B.  y=3＋4x 　　　C.  y=－3－4x 　　　D.  y=－3＋4x

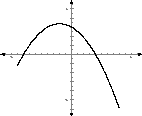
17．

（第17题）

二次函数的图象如图，那么（　　 ） A．a>0,c>0　　　  B。 a>0，c<0 C．a<0,c>o　　　  D.　 a<0, c<0

18．下列命题正确的是（　　　　 ）

A．弦是直径。　　　　　　　　  B。圆的内接平行四边形一定是矩形。

B． 长度相等的两条弧是等弧。　　 D。经过三点一定可以作圆。

19．如果两圆有且只有一条公切线，那么两圆的位置关系是（　　 ）

A． 　外切，　 B。　 相交。　　　C。　 内切。　　　 D。　　内含

20．下列命题正确的是（　　　　 ）

A． 各边都相等的六边形是正六边形。　　　　B。正n边形的中心角与外角相等。

B． 多边形是轴对称图形也是中心对称图形。

D．任意一圆一定有一个内接三角形，并且只有一个内接三角形。

三、解答题：

21．（6分）一次函数y=kx－4经过点（2，－1）。

（1）写出这个函数的解析式。

（2）设直线y=kx－4与x轴、y轴交于A、B两点，求△OAB的面积。（O为原点）

22．（6分）已知：y与成反比例，且当x=4时，y=5，

（1）　　　 求y与x的函数关系式，并确定自变量x的取值范围。

（2）　　　 判定点（6，15）是否在这个函数图象上？

23．尺规作图：（4分）

作一个⊙O，使它∠AOB的两边相切 并且与OB切于点M。（保留作图痕迹 不写作法）

24．（6分）

如图，已知AB是⊙O的直径，AC是弦，直线CE和⊙O切于 点C，AD⊥CE，垂足为D。 求证：

25．（6分）

已知：⊙与⊙外切于点A，BC是⊙和⊙ 的公切线，B、C为切点，B的延长线与CA的延长 线交于点D。 求证：点D在⊙上。 和⊙的公切线，B、C为切点。

在△ABC中，∠B=90°，D是AC上一点，以O为圆心， OB为半径的圆与AB交于点E，与AC切于点D，AD=2， CD=3。求⊙O的半径。

26．（8分）

27．（8分）现有24m长的篱笆要围成一个长方形的养鸡场，设矩形的一边长为Xm，面积为S。

（1）求出S与x之间的函数关系式，并确定自变量x的取值范围。

（2）请你设计一种方案，使这个矩形的面积最大。

28．（10分）已知二次函数，其中m为实数。

（1）　　　 求证：不论m取何实数，这个二次函数的图象与x轴必有两个交点。

（2）　　　 设这个二次函数的图象与x轴交于点A（，0），B（，0）且，的倒数和为，求这个二次函数的解析式。

初三数学半期考试卷

29．（12分）

已知：如图，BC为半圆的直径，F是半圆上异于B、C的一 点，A是BF的中点，AD⊥BC，垂足为D，BF交AD于点E，（1）求证：BE·BF=BD·BC。   （2）试比较线段BD与AE的大小，并说明道理。

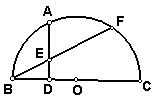
30．（12分）已知：二次函数的图象与x轴相交于（0，0），（m,0）（m≠0）两点。

（1）　　　 求这个二次函数图象的解析式。

（2）　　　 若这个二次函数图象的顶点在y=4x上，求m的值。

31．（12分）

　　　　 

	（图1）		（图2）

某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行如下讨论：

甲同学：这种多边形不一定是正多边形，如圆内接矩形；

乙同学：我发现边数是6时，它也不一定是正多边形，如图1，△ABC是正三角形，AD=BE=CF。可以证明六边形ADBECF的各内角相等，但它未必是正六边形；

丙同学：我能证明，边数是5时，它是正多边形，我想，边数是7时，它可能也是正多边形。

（1）　　　 请你说明乙同学构造的六边形各内角相等。

（2）　　　 请你证明，各内角都相等的圆内接七边形ABCDEFG（图2）是正七边形（不必写已知、求证）。

（3）　　　 根据以上探索过程，提出你的猜想（不必证明）。