初三实验班选拔考试数学试题
时量:120分钟 满分:120分
班级________ 姓名________
卷Ⅰ(卷Ⅰ共23个小题,满分100分)
一、选择题(每题只有一个正确答案,请将正确答案的序号写在题后括号内。本大题共10个小题,每小题4分,满分40分)
1.已知a的取值范围如图1所示,化简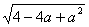 +a+1等于( )
+a+1等于( )

 A.1-2a B.3 C.-3 D.2a-1
图1
A.1-2a B.3 C.-3 D.2a-1
图1

 2.使分式
2.使分式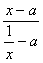 有意义的x 应满足的条件是( )-1 0 1 2
有意义的x 应满足的条件是( )-1 0 1 2
A. 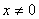 B.
B.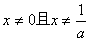
C.  D.
D.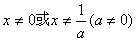
3.已知x为正整数,那么3、x、10为三边可能组成的三角形的个数为( )
A.2个 B.3个 C.5个 D.7个
4.已知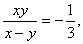 则
则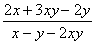 的值为( )
的值为( )
A. 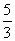 B.
B.
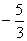 C.
C.
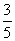 D.
D.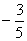
 5.如图2,AC=CD=DA=BC=DE,则ÐBAE是ÐB的(
)倍.
5.如图2,AC=CD=DA=BC=DE,则ÐBAE是ÐB的(
)倍.
A.6 B.4 C. 3
D.2
图2
6.数2002
2002 的个位数字是( )
A. 2
B. 4 C. 6 D. 8
 7.如图3,△
ABC中,∠A的平分线交BC于D,
7.如图3,△
ABC中,∠A的平分线交BC于D,
AB=AC+CD,∠C=80o,那么∠B的大小是( )
A. 20
o B. 40
o C.
50
o D. 60
o
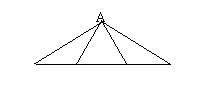
8.如图4(ⅰ),6枚硬币排成一个三角形,最少移 图3
动几枚硬币可以排成图(ⅱ)所示的图形? ( )


 (ⅰ) 图4
(ⅱ)
(ⅰ) 图4
(ⅱ)
A. 2个 B. 3个 C.5个 D.7个
9.如图5,工作流程线上A、B、C、D处各有1名工人,现要求在流程线上安放一个工具箱,使4个人到工具箱的距离之和最短,则工具箱安放的位置( )。图5 
A.只能是A或B
B.只能是线段BC的中点
C.是线段AB或CD内的任意一点处 D.是线段BC上的任意一点处
10.一条轮船从A港到B港顺水航行需6小时,从B港到A港逆水航行需8小时,若在静水条件下,从A港到B港需( )小时。
A. 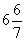 B.
B. 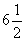 C. 7
D.
C. 7
D. 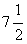
二、填空题(本大题共10个小题,每小题4分,满分40分)
11.分解因式:4x2y2-(z2-x2-y2)2=_____________________.
12.已知x= 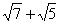 , y =
, y = 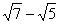 ,则x2-xy+y2=___.
,则x2-xy+y2=___.
13.若x-y+2与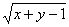 互为相反数,则x=_____,y=____.
互为相反数,则x=_____,y=____.
14.已知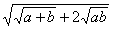 =
=  (a≥b≥0),则
(a≥b≥0),则
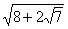 =_________,
=_________,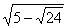 =__________.
=__________.
15.已知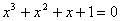 ,则1+x+x2+x3+…+x2002+x2003=___.
,则1+x+x2+x3+…+x2002+x2003=___.
16.已知A1B1C1D1是等腰梯形ABCD四边中点所构成的四边形,那么由A1B1C1D1四边中点所构成的四边形一定是_______四边形.
 17.如图6,已知AB=BC=CD=DE=EF,
17.如图6,已知AB=BC=CD=DE=EF,
若ÐA=12°13¢12²,则ÐFED=______. 图6
18.如图7,正方形ABCD的对角线相交于点O,点O是正方形A¢B¢C¢D¢的一个顶点,如果两个正方形的边长均为1,则图中四边形EBFO的面积是_____________.




图7
图8
19.方程x2=11+y2的正整数解是____________________.
20. 如图8,一牧童在A处牧马,牧童家在B处,A、B处距河岸分别为300米和500米,CD=600米。天黑前,牧童从A处将马赶到河边饮水后再赶回家,那么牧童最少要走_______ 米。
三、先阅读下列内容,再答题(本大题满分6分)
 21.三角形中边与角之间的不等关系定理:在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大。即△ABC中,如果ÐC > ÐB,那么AB > AC.(如图9)
21.三角形中边与角之间的不等关系定理:在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大。即△ABC中,如果ÐC > ÐB,那么AB > AC.(如图9)
1.
如果一个三角形中最大的边所对的角是锐角,
那么这个三角形一定是___________三角形。
图9
2.
在△ABC中,已知BC > AB
> AC,那么ÐA、ÐB、ÐC有怎样的大小关系?
3.
在△ABC中,ÐA=70°,ÐB=50°,那么AB、BC、AC之间有怎样的大小关系?
4.
直角三角形的哪一条边最长?为什么?
四、先阅读下列内容,再证明(本大题满分7分)
22.能够表示成 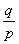 (p与q是互质的整数)的数称为有理数,那么不能表示成
(p与q是互质的整数)的数称为有理数,那么不能表示成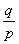 的数就叫做无理数。先阅读下列证明
的数就叫做无理数。先阅读下列证明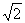 是无理数的过程,再进行证明。
是无理数的过程,再进行证明。
假设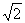 =
= 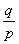 (p与q是互质的整数),于是q=
(p与q是互质的整数),于是q=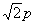 ,两边平方得p2=2q2.于是p2是偶数,由于只有偶数的平方才能是偶数,所以p也是偶数。设p=2s,s是整数,则4s2=2q2,即q2=2s2,因此q是偶数,所以p和q都是偶数,一定有公约数2,这与p、q 的最大公约数是1矛盾.因此
,两边平方得p2=2q2.于是p2是偶数,由于只有偶数的平方才能是偶数,所以p也是偶数。设p=2s,s是整数,则4s2=2q2,即q2=2s2,因此q是偶数,所以p和q都是偶数,一定有公约数2,这与p、q 的最大公约数是1矛盾.因此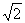 不能表示成分数的形式,即
不能表示成分数的形式,即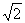 不是有理数.
不是有理数.
试判断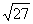 + 1是有理数还是无理数?并证明你的结论.
+ 1是有理数还是无理数?并证明你的结论.
五、证明题(本大题满分7分)
23. 如图10,△ABC三边上的高、中线和该边所对的角的角平分线都互相重合,AE=CD,AD、BE相交于P,BQ⊥AD于Q,

求证:ÐPBQ=30°.
图10
卷Ⅱ(卷Ⅱ共两个小题,每小题10分)
24.如图11,△ABC中,BC=10㎝,BC边上的高h=15㎝,
(1) 如图11-1,若D1、D2是AB上的三等分点,E1、E2是AC上的三等分点,求四边形D1E1E2D2的面积。
(2) 如图11-2,若D1、D2、D3、D4是AB上的五等分点,E1、E2、E3、E4是AC上的五等分点,求四边形D2E2E3D3的面积。
(3)如图11-3,若D
1、…D
n、D
n+1、…、D
2n是AB上的2n+1等分点,E
1、…E
n、E
n+1、…、E
2n是AC上的2n+1等分点,求四边形D
nE
nE
n+1D
n+1的面积。




(1)
(2)
(3)
图11
25、猜测并证明
(1)试猜测,当 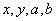 满足什么条件(只写一种你认为正确的条件)时,
满足什么条件(只写一种你认为正确的条件)时, 和
和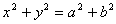 能同时成立.
能同时成立.
(2)若 且
且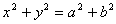 ,求证x2002+y2002=a2002+b2002
,求证x2002+y2002=a2002+b2002
![]() +a+1等于( )
+a+1等于( )![]()
![]() A.1-2a B.3 C.-3 D.2a-1
图1
A.1-2a B.3 C.-3 D.2a-1
图1![]()
![]() 2.使分式
2.使分式![]() 有意义的x 应满足的条件是( )-1 0 1 2
有意义的x 应满足的条件是( )-1 0 1 2 ![]() B.
B.![]()
![]() D.
D.![]()
![]() 则
则![]() 的值为( )
的值为( )![]() B.
B.
![]() C.
C.
![]() D.
D.![]()
 5.如图2,AC=CD=DA=BC=DE,则ÐBAE是ÐB的(
)倍.
5.如图2,AC=CD=DA=BC=DE,则ÐBAE是ÐB的(
)倍. 7.如图3,△
ABC中,∠A的平分线交BC于D,
7.如图3,△
ABC中,∠A的平分线交BC于D, 

![]() (ⅰ) 图4
(ⅱ)
(ⅰ) 图4
(ⅱ)![]()
![]() B.
B. ![]() C. 7
D.
C. 7
D. ![]()
![]() , y =
, y = ![]() ,则x2-xy+y2=___.
,则x2-xy+y2=___.![]() 互为相反数,则x=_____,y=____.
互为相反数,则x=_____,y=____.![]() =
= ![]() (a≥b≥0),则
(a≥b≥0),则![]() =_________,
=_________,![]() =__________.
=__________.![]() ,则1+x+x2+x3+…+x2002+x2003=___.
,则1+x+x2+x3+…+x2002+x2003=___.![]() 17.如图6,已知AB=BC=CD=DE=EF,
17.如图6,已知AB=BC=CD=DE=EF,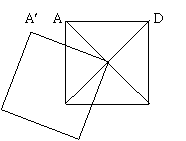
![]()
![]()
![]()
![]() (p与q是互质的整数)的数称为有理数,那么不能表示成
(p与q是互质的整数)的数称为有理数,那么不能表示成![]() 的数就叫做无理数。先阅读下列证明
的数就叫做无理数。先阅读下列证明![]() 是无理数的过程,再进行证明。
是无理数的过程,再进行证明。![]() =
= ![]() (p与q是互质的整数),于是q=
(p与q是互质的整数),于是q=![]() ,两边平方得p2=2q2.于是p2是偶数,由于只有偶数的平方才能是偶数,所以p也是偶数。设p=2s,s是整数,则4s2=2q2,即q2=2s2,因此q是偶数,所以p和q都是偶数,一定有公约数2,这与p、q 的最大公约数是1矛盾.因此
,两边平方得p2=2q2.于是p2是偶数,由于只有偶数的平方才能是偶数,所以p也是偶数。设p=2s,s是整数,则4s2=2q2,即q2=2s2,因此q是偶数,所以p和q都是偶数,一定有公约数2,这与p、q 的最大公约数是1矛盾.因此![]() 不能表示成分数的形式,即
不能表示成分数的形式,即![]() 不是有理数.
不是有理数.![]() + 1是有理数还是无理数?并证明你的结论.
+ 1是有理数还是无理数?并证明你的结论. 求证:ÐPBQ=30°.
求证:ÐPBQ=30°.



![]()
![]() 满足什么条件(只写一种你认为正确的条件)时,
满足什么条件(只写一种你认为正确的条件)时,![]() 和
和![]() 能同时成立.
能同时成立.![]() 且
且![]() ,求证x2002+y2002=a2002+b2002
,求证x2002+y2002=a2002+b2002