初三数学总复习测试方程、不等式
班级 姓名 学号 得分
一、选择题(本题共有12个小题,每小题都有A、B、C、D四个选项,请你把你认为适当的选项前的代号填入题后的括号中,每小题4分,共48分)
1、下列方程有实数根的是( )(2001吉林)
A 2x2+x+1=0 B x2―x―1=0 C x2―6x+10=0 D x2―![]() x+1=0
x+1=0
2、方程2x2+3x―1=0的两根为x1,x2,则![]() 的值为(
)(2001吉林)
的值为(
)(2001吉林)
A 3 B ―3 C ―![]() D
D ![]()
3、下面不等式无解的是( )(2001青海)
A ![]() B
B ![]() C
C ![]() D
D ![]()
4、若方程组![]() 的解x,y满足0<x―y<1,则k的取值范围是(
)(2001山东)
的解x,y满足0<x―y<1,则k的取值范围是(
)(2001山东)
A 2<k<3 B 2<k<4 C ―4<k<0 D ―4<k<―2
5、一项工程,甲独立完成需要10天,乙独立完成需要15天,现在两人合作,完工后厂家共付给450元。如果按完成工程量的多少进行分配,则甲、乙二人各分得( )(2001山东烟台)
A 250元,200元 B 260元,190元 C 265元,185元 D 270元,180元
6、解方程6(x2+![]() )+5(x+
)+5(x+![]() )=38,若设x+
)=38,若设x+![]() =y,则原方程变为(
)(2001山东烟台)
=y,则原方程变为(
)(2001山东烟台)
A 6y2+5y―26=0 B 6y2+5y―38=0 C 6y2+5y―40=0 D 6y2+5y―50=0
7、方程组![]() 实数解的个数是( )(2001山东临沂)
实数解的个数是( )(2001山东临沂)
A 0 B 1 C 2 D 3
8、若不等式组![]() 的解集为x>3,则m的取值范围是(
)(2001山东威海)
的解集为x>3,则m的取值范围是(
)(2001山东威海)
A m≥3 B m=3 C m<3 D m≤3
9、若α、β是方程x2+2x―2001=0的两个实数根,则α2+3α+β=( )(2001山东威海)
A ―2000 B 2000 C 1999 D 2001
10、方程![]() 的解是(
)(2001浙江湖州)
的解是(
)(2001浙江湖州)
A 2 B ±2 C 16 D ±16
11、若实数a、b满足a2―8a+5=0,b2―8b+5=0,则![]() 的值为( )(2001湖北十堰)
的值为( )(2001湖北十堰)
A ―20 B 2 C 2或―20 D 2或20
12、甲、乙两班学生参加植树造林,已知甲班每天比乙班多种5棵树,甲班种80棵所用的天数比乙班种70棵所用的天数相等,若设乙班每天种树x棵,则根据题意列出的方程是( )(2001北京西城)
A ![]() B
B ![]() C
C ![]() D
D ![]()
二、填空题(本题共有6个小题,每小题5分,共30分)
13、若![]() 是方程x―ky=1的解,则k=
(2001江苏盐城)
是方程x―ky=1的解,则k=
(2001江苏盐城)
14、关于x的方程3x+2a=0的根是2,则a等于 (2001江苏南京)
15、无理方程![]() 的解是
(2001广东茂名)
的解是
(2001广东茂名)
16、已知x1、x2是方程x2+4x―3=0的两个根,则(x1+1)(x2+1)的值是 (2001湖南常德)
17、不等式组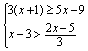 的正整数解是
(2001山东)
的正整数解是
(2001山东)
18、已知方程x2―2![]() x+1=0,求一个一元二次方程,使它的根分别是原方程各根的倒数,则这个一元二次方程是
(2001湖北荆门)
x+1=0,求一个一元二次方程,使它的根分别是原方程各根的倒数,则这个一元二次方程是
(2001湖北荆门)
三、解答题(本题共7个小题,其中19、20小题每题8分,21、22小题每题10分,22、23小题每题12分,25小题14分,共72分)
19、解方程:![]() (2001北京西城)
(2001北京西城)
20、解方程组![]() (2001山东)
(2001山东)
21、新世纪第一个“五一”旅游黄金周已结束,据有关统计报道,5月1日至7日,全省各景区、景点共接待省内、省外旅游者122万人次,旅游总收入达48000万元,其中省内、省外旅游者人均消费各达到160元和1200元,求出省内、省外旅游者的人次(答案以万人次为单位且保留整数位)(2001青海)
22、已知关于x的方程2x2―2x+m=0
(1)m取什么值时,方程有两个不相等的实数根?
(2)设x1,x2是方程的两个根,且x12+x22=4,求方程的根(2001福建三明)
![]() 23、某初一学生在做作业时,不慎将墨水瓶打翻,使一道作业题只看到如下字样:“甲、乙两地相距40千米,摩托车的速度为45千米/时, ?”(涂黑部分表示被墨水覆盖的若干文字)请将这道作业题补充完整,并列方程解答(2001吉林)
23、某初一学生在做作业时,不慎将墨水瓶打翻,使一道作业题只看到如下字样:“甲、乙两地相距40千米,摩托车的速度为45千米/时, ?”(涂黑部分表示被墨水覆盖的若干文字)请将这道作业题补充完整,并列方程解答(2001吉林)
24、已知a是非零整数,且满足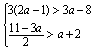 ,解关于x的方程x2―3x+3
,解关于x的方程x2―3x+3![]() =10a(2001湖北天门)
=10a(2001湖北天门)
25、已知方程组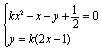 (x、y为未知数)有两个不同的实数解
(x、y为未知数)有两个不同的实数解![]() ,
,![]() 。
。
(1)求实数k的取值范围
(2)如果y1y2+![]() =3,求实数k的值(2001江苏盐城)
=3,求实数k的值(2001江苏盐城)