2005—2006学年度初三(实验班)第三次月考测试试卷
姓名 学号 成绩
一.选择题(每题3分,共30分,把正确的答案填在下面的答题表内,否则不给分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1.已知一元二次方程的两根分别为![]() ,
, ![]() , 则这个方程为
, 则这个方程为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2.已知点P(![]() ,
,![]() )在第四象限,则
)在第四象限,则![]() 的取值范围是
的取值范围是
A、 ![]() B、
B、 ![]() C、
C、 ![]() D、
D、 ![]()
3.如果一元二次方程![]() 的两根为
的两根为![]() ,
,![]() ,则
,则![]() ·
·![]() 的值等于
的值等于
A、
0
B、 2 C、 ![]() D、
D、 ![]()
4.下列命题中:(1)经过一点可以作无数个圆;(2)经过两点只能作一个圆;(3)经过三点一定可以作一个圆;(4)三角形有且只有一个外接圆;(5)圆有且只有一个内接三角形;(6)三角形的外心到三边的距离相等;(7)三角形的外心是三条角平分线的交点;正确的个数有
A、 2个 B、 3个 C、 4个 D、 5个
5.已知在Rt△ABC中,∠C = 90º,![]() ,则
,则![]() 的值等于
的值等于
A、 B、 C、 D、 1
6.圆内接四边形ABCD的四个内角![]() 可能是
可能是
A ![]() B
B ![]() C
C ![]() D
D ![]()
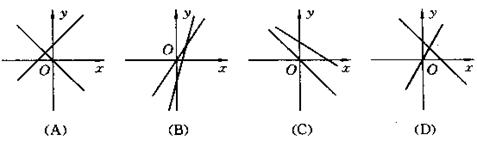
7.下图中表示一次函数![]() 与正比例函数
与正比例函数![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() )图像的是
)图像的是
 |
8、下列命题中:(1)垂直平分弦的直线经过圆心;(2)平分弦的直径垂直于弦,并且平分弦所对的两条弧;(3)平分圆的的两条弧的直线必过圆心;(4)平行弦所夹的两条弧相等;(5)垂直于弦的直径平分弦,并且平分弦所对的两条弧;其中正确的有
A、 1个 B、 2个 C、 3个 D、 4个
9.⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,则⊙O的半径为
 A、 4 cm B、 5 cm C、 8 cm D、 10 cm
A、 4 cm B、 5 cm C、 8 cm D、 10 cm
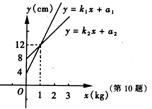
10.已知甲,乙两弹簧的长度![]() (cm)与所挂物体质量
(cm)与所挂物体质量
![]() (kg)之间的函数解析式分别为
(kg)之间的函数解析式分别为![]() 和
和![]() ,
,
图象如下图,设所挂物体质量均为2kg时,甲弹簧长为![]() ,乙
,乙
弹簧长为![]() 则
则![]() 与
与![]() 的大小关系为
的大小关系为
A ![]() >
>![]() B
B ![]() =
=![]() C
C ![]() <
<![]() D 不能确定
D 不能确定
二、填空题(每小题4分,共32分)
11.函数![]() 中,自变量
中,自变量![]() 的取值范围是___________;
的取值范围是___________;
12.平面直角坐标系内点P(–2,0)与点Q(3,0)之间的距离是___________;
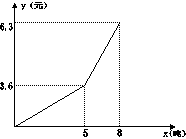 13.今年入夏以来,全国大部分地区发生严重干旱,某市自来水公
13.今年入夏以来,全国大部分地区发生严重干旱,某市自来水公
司为了鼓励市民节约用水,采取分段收费标准,若某户居民每月应
交水费![]() (元)是用水量
(元)是用水量![]() (吨)的函数,其图像如图所示,
(吨)的函数,其图像如图所示,
(1)分别写出![]() ≤5和
≤5和![]() 5时,
5时,![]() 与
与![]() 的函数解析式
的函数解析式
 ①
②
;
①
②
;
14.如图一,在△ABO中,∠AOB=90°,
∠B=25°,以O为圆心,OA为半径的圆交AB于D,
![]() 则
则![]() 的度数是
; (图一)
的度数是
; (图一)
 15.1998年我国粮食产量为49000万吨,如果到2000年我国粮食产量达到59290万吨,设平均年增长率为
15.1998年我国粮食产量为49000万吨,如果到2000年我国粮食产量达到59290万吨,设平均年增长率为![]() ,列方程为:
;
,列方程为:
;
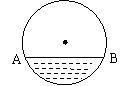
16、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示;
 若油面宽AB = 600mm,则油的最大深度为__________mm;
若油面宽AB = 600mm,则油的最大深度为__________mm;
17、如图,破残的轮片上,弓形的弦AB为4cm,高CD为1cm,
则轮片的直径为____ ____cm;
18、已知⊙O的半径为5,弦AB//CD,AB = 6,CD = 8,则
AB和CD间的距离等于______________;
三、解答题(本题共8小题,共88分)
19(本题10分)、计算:sin45º·cos45º – 3tan30º + tan45º + sin60º
20(本题10分)、解方程:![]()
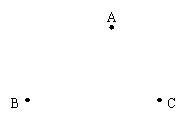
21(本题8分)、如图,A、B、C是三个城市,现要建一条环城高速公路,要求公路要经过每一个城市,且是圆形,请画出公路的路线图;(要求尺规作图,不写出作法,保留作图痕迹)
22.(14分)小红把过年的压岁钱![]() 元存入银行后,准备以后每月从平时的部分零用钱中节约
元存入银行后,准备以后每月从平时的部分零用钱中节约![]() 元存在银行,小林听说后,表示从现在起每月存
元存在银行,小林听说后,表示从现在起每月存![]() 元,争取超过小红,他们各自存款余额的总数
元,争取超过小红,他们各自存款余额的总数![]() (元)与存款时间
(元)与存款时间![]() (月)的关系如图所示:
(月)的关系如图所示:
(1)根据图象回答:半年以后小林的存款总数是多少?能否超过小红?至少几个月后小林的存款能超过小红?
(2)根据图象提供的信息,求出他们二人各自存款余额的总数![]() (元)与存款时间
(元)与存款时间![]() (月)的关系式,验证你在(1)中的结论;
(月)的关系式,验证你在(1)中的结论;
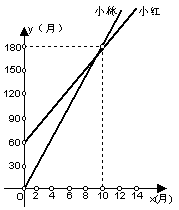 |
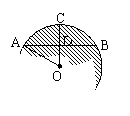
 23(本题10分)已知,如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点;求证:MC = NC;
23(本题10分)已知,如图,OA、OB、OC是⊙O的三条半径,∠AOC=∠BOC,M、N分别是OA、OB的中点;求证:MC = NC;
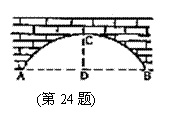 24(本题12分)有一个拱桥是圆弧形,他的跨度为60
24(本题12分)有一个拱桥是圆弧形,他的跨度为60![]() ,拱高为18
,拱高为18![]() ,当洪水泛滥跨度小于30
,当洪水泛滥跨度小于30![]() 时,要采取紧急措施。若拱顶离水面只有4
时,要采取紧急措施。若拱顶离水面只有4![]() 时,问是否要采取紧急措施?
时,问是否要采取紧急措施?
 25.(12分)如图,
25.(12分)如图,![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .(1)求证:
.(1)求证:![]() ;(2)如果
;(2)如果![]() ,求
,求![]() 的长
的长
26(本题12分)已知:如图(1),AB是⊙O的直径,直线![]() 和⊙O相交于C、D,AE⊥
和⊙O相交于C、D,AE⊥![]() ,垂足为E,BF⊥
,垂足为E,BF⊥![]() ,垂足为F;
,垂足为F;
(1)求证:EC = DF
(2)若把直线![]() 向上平移与AB相交于点P(不与O重合),那么结论(1)是否还成立?画出图形并写出证明过程;
向上平移与AB相交于点P(不与O重合),那么结论(1)是否还成立?画出图形并写出证明过程;
 |
参考答案:
一.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | A | A | A | A | D | C | C | B | A |
二.
11.![]() ;
;
12.![]() ;
;
13.![]() ,
,![]() ;
;
14.![]() ;
;
15.![]() ;
;
16.![]() ;
;
17.![]() ;
;
18.![]() 或
或![]() ;
;
三.
19.原式![]()
20.换元后![]() ,此时关于
,此时关于![]() 的方程无实数根;
的方程无实数根;![]() 时,
时,![]() ,
,![]() ,缺检验扣1分;
,缺检验扣1分;
21.要求铅笔作图,钢笔、其他笔作图扣一半,无结论扣1分;
22.(1)半年后小林的存款总数为![]() 元,不能超过小红,至少10个月后小林的存款能超过小红。(2)小红:
元,不能超过小红,至少10个月后小林的存款能超过小红。(2)小红:![]() ,小林:
,小林:![]() ,验证:略。
,验证:略。
23.运用“边角边”证三角形全等后得到对应边相等:
24.解:作出圆弧形的圆心O,
在Rt⊿OAD中,
![]() ,而OA =
,而OA =![]() ,AD = 30,CD = 18
,AD = 30,CD = 18
∴![]()
∴![]()
当拱顶里水面![]() 米时,水面所在弦的弦心距为:
米时,水面所在弦的弦心距为:
![]() 米,设水面所在的弦为
米,设水面所在的弦为![]() ,由勾股定理可知:
,由勾股定理可知:
![]() ,∴
,∴![]() ,负值舍去,∴
,负值舍去,∴![]()
![]()
∴不用采取紧急措施。
25.
 解:(1)延长AF交⊙O于G,连结BG;
解:(1)延长AF交⊙O于G,连结BG;
∵AE⊥BD于E;
∴弧AB = 弧BG
∴∠BAG =∠BGA
∵弧AB = 弧AB
∴∠G =∠C
∴∠BAF =∠C;
(2)在⊿ABF和⊿ABC中;
∵∠FBA =∠CBA
∵∠BAF =∠C
∴⊿ABF∽⊿ABC
∴![]()
∵BF = 6,BC = 2
∴![]()
 26.
26.
解:(1)作OG⊥EF
在⊙O中,∵OG⊥EF
∴CG = DG
∵OG⊥EF,AE⊥![]() ,BF⊥
,BF⊥![]() ,
,
∴AE∥OG,AE∥BF,
∴AE∥OG∥BF
∴四边形AEFB是直角梯形;
∵O为AB中点,
∴G为EF的中点,
∴EG = FG
∴![]()
∴EC = DF
(2)若把直线![]() 向上平移与AB相交于点P
向上平移与AB相交于点P
 (不与O重合),那么结论(1)仍然成立;
(不与O重合),那么结论(1)仍然成立;
证明:作OG⊥EF
在⊙O中,∵OG⊥EF
∴CG = DG
∵OG⊥EF,AE⊥![]() ,BF⊥
,BF⊥![]() ,
,
∴AE∥OG,AE∥BF,
∴AE∥OG∥BF
∵OA = OB
∴GE = GF(平行线等分线段定理)
∴![]()
∴EC = DF