初三数学总复习测试十七模拟试卷四
学校 班级 姓名 学号 得分
说明:本试卷共三大题,25小题,满分150分,考试时间为100分钟。答案一律做在答题卷相应的位置上,做在试卷上无效。
卷 一
一、选择题
1、4的算术平方根是( )
A 2 B ―2 C ±2 D 16
2、对有理数230800精确到万位,用科学记数法表示为( )
A 23 B 2.3×105 C 2.31×105 D 23×104
3、已知圆锥的侧面展开图是![]() 圆,其母线长为15cm,则该圆锥的侧面积为( )
圆,其母线长为15cm,则该圆锥的侧面积为( )
A 75πcm2 B 100πcm2 C 225πcm2 D 300πcm2
4、函数![]() 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A x<2 B x≤2 C x<2且x≠0 D x≤2且x≠0
5、直径分别是4cm,6cm的两圆圆心距为10cm,则这两圆共有公切线( )
A 1条 B 2条 C 3条 D 4条
6、已知4x―7y=0,则x∶y=( )
A 4∶7 B ―4∶7 C 7∶4 D ―7∶4
7、小李、小王、小张三人任意排成一行拍照,小李和小王彼此相邻的概率是( )
 A
A ![]() B
B ![]() C
C ![]() D
D ![]()
8、如图,在长方体中,与棱AA1平行的面有( )
A 1个 B 2个 C 3个 D 4个
9、设多项式x2+kx―18在整数范围内能分解因式,则可以取的整数值有( )
A 3个 B 4个 C 6个 D 8个
![]() 10、如图, ABCD中,E为AD中点,已知AB=2cm,BC=2cm,
10、如图, ABCD中,E为AD中点,已知AB=2cm,BC=2cm,
∠ABC=60°,则图中阴影部分面积有( )
A ![]() cm2 B 1cm2 C
cm2 B 1cm2 C ![]() cm2 D 6cm2
cm2 D 6cm2
 11、某种商品因换季进行降价处理,如果按定价的七五折出售,将赔25元;如果按定价的九折出售,还能赚20元,问这种商品的定价是( )
11、某种商品因换季进行降价处理,如果按定价的七五折出售,将赔25元;如果按定价的九折出售,还能赚20元,问这种商品的定价是( )
A 100元 B 200元 C 300元 D 500元
12、如图,⊙O中AB为直径,AD是弦,过点B的切线与AD的延长线
交于点C,若AD=CD,则sin∠ACO等于( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
卷 二
二、填空题
13、当a=
时,![]() =0。
=0。
 14、已知数据x1、x2、x3、x4、…x10的平均数为9,方差为2,则数据3x1、3x2、3x3…、3x10的方差为
。
14、已知数据x1、x2、x3、x4、…x10的平均数为9,方差为2,则数据3x1、3x2、3x3…、3x10的方差为
。
15、如图,AB=AC,要使△ABE≌△ACD,则还需要添加一个
条件是 。(只写出一组即可)
16、满足条件![]() ,则m的非负整数值是
。
,则m的非负整数值是
。
 17、已知a、b满足a2―2a―1=0,b2―2b―1=0,且a≠b,则
17、已知a、b满足a2―2a―1=0,b2―2b―1=0,且a≠b,则![]() 的值为 。
的值为 。
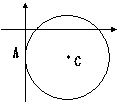
18、如图,在直角坐标系中,⊙C与y轴切于负半轴上的点A,
与x轴相交于点(1,0),(9,0),则以点C关于x轴的对称
点坐标为 。
三、解答题
19、计算:―22+2cos45°―(1―![]() )―1+(π―4)0―
)―1+(π―4)0―![]() +∣―3∣
+∣―3∣
20、已知x=![]() ,求
,求![]() 的值
的值
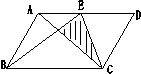
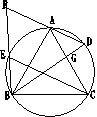 21、如图,△ABC是⊙O的内接正三角形,D是AC上任一点,过C作CE∥AD,交⊙O于点E,BE、DA的延长线相交于点F,连BD交AC于点G,
21、如图,△ABC是⊙O的内接正三角形,D是AC上任一点,过C作CE∥AD,交⊙O于点E,BE、DA的延长线相交于点F,连BD交AC于点G,
求证:(1)△BDF是正三角形
(2)BC2=BG·BF
22、某科技公司研制一种新产品,决定向银行贷款200万资金用于生产这种产品。签字的合同上约定:两年到期时一次性还本付息,利息为本金的8%,该产品投放市场后,由于产销对路,使公司在两年到期时除还清贷款的本金和利息外,还赢余72万元。若该公司在生产期间每年比上一年资金增长的百分率相同,试求这个百分率
23、阅读下列材料:
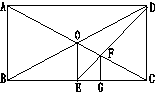 已知:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连结DE,交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点
已知:如图,矩形ABCD中,AC、BD相交于点O,OE⊥BC于E,连结DE,交OC于点F,作FG⊥BC于G,求证:点G是线段BC的一个三等分点
(1)补全证明过程:
∵ 在矩形ABCD中,OE⊥BC,DC⊥BC
∴ OE∥BC
∵ ![]()
∴ ![]()
(2)请你仿照上面的画法,在原图上画出BC的一个四等分点(要求:保留画图痕迹,不写画法及证明过程)
(3)设矩形ABCD的面积为4S,若仿照上面的画法不断画下去,得到BC的一个10等分点M,连DM与OC交于点N,则S△CDN= 。
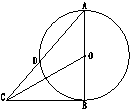
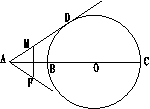
24、如图,⊙O的割线ABC过点O,AD切⊙O于D,sin∠DAC=![]() ,AB是方程x2+2x+2
,AB是方程x2+2x+2![]() =10的一个正根,
=10的一个正根,
(1)求⊙O的半径及AD的长
(2)若M为AD上任一点(点M与A、D重合),ME⊥AC于E,延长ME至点F,使EF=ME,猜想直线AF与⊙O的位置关系,并给予证明
 (3)连OF、OD,设AM=x,四边形MFOD的面积为y,求y关于x的函数解析式,并求当AM多长时,四边形MFOD的面积最大?最大面积是多少?
(3)连OF、OD,设AM=x,四边形MFOD的面积为y,求y关于x的函数解析式,并求当AM多长时,四边形MFOD的面积最大?最大面积是多少?
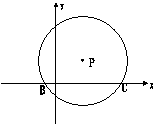
25、如图,抛物线y=ax2+bx+c (a<0)的顶点A在以P(1,1)为圆心,2为半径的圆上,且经过⊙P与x轴的两个交点B、C,
(1)求抛物线的解析式
(2)求⊙P的弦AC在第一象限内形成的弓形面积
(3)抛物线上能否找到一点D,使DP与OA互相平分?如果有,求出D点的坐标;如果没有,请说明理由
(4)若第(3)小题能找到点D,求出直线AD上的点M,使△APM为等腰三角形;若第(3)小题不能找到点D,求出直线AB上的点M,使△APM为等腰三角形。