初三数学总复习测试十九模拟试卷六
班级 姓名 学号 得分
一、选择题
1、―4÷2的值等于( )
A 2 B 8 C ―2 D ―8
2、计算2tg30°的结果为( )
A 1 B 2![]() C
C ![]() D
D ![]()
![]()
3、等腰三角形的顶角是70°,那么这个等腰三角形的一个底角等于( )
A 55° B 60° C 65° D 70°
4、已知一个样本为4,0,2,1,―2,那么样本平均数为( )
A 2 B 1.5 C 1.2 D 1
5、圆台的轴截面是( )
A 矩形 B 等腰梯形 C 等腰三角形 D 扇形
6、![]() 与
与![]() 的关系是(
)
的关系是(
)
A 互为倒数 B 互为负倒数 C 互为相反数 D 相等
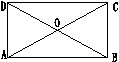 7、如图,在矩形ABCD中,AB=4,AC=5,O是对角线AC、BD
7、如图,在矩形ABCD中,AB=4,AC=5,O是对角线AC、BD
的交点,那么△AOB的周长等于( )
A 12 B 10 C 9 D 8
 8、函数
8、函数![]() 的图像经过点(1,2),那么函数y=kx+1的图像不经过( )
的图像经过点(1,2),那么函数y=kx+1的图像不经过( )
A 第一象限 B 第二象限 C 第三象限 D 第四象限
9、已知两圆的半径分别为2,5,而圆心距是一元二次方程x2―10x+21=0
的根,则两圆的公切线有( )
A 1条 B 3条 C 4条 D 1条或3条
10、如图,PA切⊙O于点A,PBC是⊙O的割线,如果PB=BC=2,那么PA的长为( )
 A 2
A 2![]() B 2 C 8 D 4
B 2 C 8 D 4
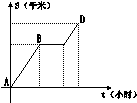
11、某人从甲地出发骑摩托车到乙地,途中因车出故障而停车修理,
到达乙地正好用了2小时,已知摩托车行驶路程S(千米)与 30
行驶时间t(时间)之间的函数关系由如图的图像ABCD给出。
若这辆摩托车修车前后行驶速度不变,且平均每行驶100千米 1 1.5 2
的耗油量为3升,根据图中给出的信息,从甲地到乙地共耗油( )
A 1.5升 B 1.35升 C 1升 D 0.9升
12、若二次函数y=ax2+bx+c(a≠0)图像顶点在第一象限,且经过点(―1,0)和点(0,1),则S=a+b+c的值的取值范围是( )
A 0<S<2 B 0<S<1 C 1<S<2 D ―1<S<1
二、填空题
13、分解因式:2ab―b2―a2+16= 。
14、已知一元二次方程kx2―2k―1x+k=0有两个不相等的实数根,那么k的取值范围是
15、研究下列算式,你会发现有什么规律?
1=12,1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,……,
请你将找出的规律用公式表示出来: 。
16、小申以两种形式储蓄500元,第一种的年利息为3.7%,第二种的年利息为2.25%,一年后得到利息为15.6元,那么小申以这两种形式储蓄的钱分别是 。
![]()
![]()
![]()
![]()
 17、已知实数x满足
17、已知实数x满足![]() ―2=x2+3x,则x2+3x―11= 。
―2=x2+3x,则x2+3x―11= 。
18、如图,A、B、C、D是圆周的四点,且AB+CD=AD+BC,如果弦AB的长为8,弦DC的长为4,那么图中两个弓形(阴影部分)面积的和是 。(π取3)
三、解答题
19、计算:∣1―![]() ∣+(sin45°―
∣+(sin45°―![]() )0+
)0+![]() ―(
―(![]() )―1
)―1
 20、如图,在直角梯形ABCD中,∠ABC=90°,∠CAD=60°,AB∥CD,E为AC的中点,且AD=CD,求证:(1)EB∥AD(2)BC=ED
20、如图,在直角梯形ABCD中,∠ABC=90°,∠CAD=60°,AB∥CD,E为AC的中点,且AD=CD,求证:(1)EB∥AD(2)BC=ED
21、某新建油罐装满油后发现底部匀速向外漏油,为安全并减少损失,需将油抽干后进行修理。现有同样功率的小型油泵若干台,若5台一起抽需10小时抽干;若7台一起抽需8小时抽干;现要在3小时内将油罐抽干,至少需要多少台抽油泵一起抽?
22、在直角坐标系中,点A的坐标是(2,1),AC⊥x轴于C,B(0,y)是正半轴(不包括原点O)上一个动点,以AB为直径的圆始终与x轴相交,设靠近原点O的一个交点为P(x,0),又设四边形ABOC的面积为S,
求(1)S关于x的函数关系式
(2)当点B在什么位置时,S最大?此时四边形ABOC是什么四边形?
 23、现要把一块如图所示的直角三角形果园地承包给甲、乙、丙三家村民,已知甲、乙、丙三家人口分别为2人,3人,5人,果园地分配办法按人口比例,并要求每家果园地均有一部分紧靠水渠一边AB,C点处是三家合用的肥料仓库,所以C点必须是三家果园地的交界处。若△ABC中,∠C=90°,AC=60米,cosA-=0.6,(1)请计算出每家应承包的果园地面积(2)用尺规在图中作出各家果园地的分界线。(不写作法,保留痕迹,并标出户名)
23、现要把一块如图所示的直角三角形果园地承包给甲、乙、丙三家村民,已知甲、乙、丙三家人口分别为2人,3人,5人,果园地分配办法按人口比例,并要求每家果园地均有一部分紧靠水渠一边AB,C点处是三家合用的肥料仓库,所以C点必须是三家果园地的交界处。若△ABC中,∠C=90°,AC=60米,cosA-=0.6,(1)请计算出每家应承包的果园地面积(2)用尺规在图中作出各家果园地的分界线。(不写作法,保留痕迹,并标出户名)
 24、如图,Rt△ABC中,∠ABC=90°,斜边AC=5,BD⊥AC于D,过C、D两点的圆交BC的延长线于点E,交AE于点F,且DF∥AB,如果AB、CB(AB>BC)的长分别是一元二次方程x2―(2m―1)x+4(m―1)=0的两根,
24、如图,Rt△ABC中,∠ABC=90°,斜边AC=5,BD⊥AC于D,过C、D两点的圆交BC的延长线于点E,交AE于点F,且DF∥AB,如果AB、CB(AB>BC)的长分别是一元二次方程x2―(2m―1)x+4(m―1)=0的两根,
(1)求m的值
(2)求线段AE与AF的长
(3)求sin∠CAE的值
25、在直角坐标系xoy中,已知点A、B、C的坐标分别为A(―2,0),B(1,0),C(0,―2![]() ),
),
(1)求经过点A、B、C三点的二次函数的解析式,并指出顶点D的坐标
(2)在y轴上求一点P,使PA+PD最小,求出点P的坐标
(3)在坐标平面中,是否存在点M,使AC为等腰△ACM的一边,且底角为30°。如果存在,请求出点M的坐标;如果不存在,请说明理由。
