八年级(下)数学期末综合练习卷（一）
测试时间90分钟 测试分值100分 学生姓名 实际评分
一、选择题(每小题3分，共30分)
1、为了了解某校初三年级400名学生的体重情况, 从中抽查了50名学生的体重进行统计分析, 在这个问题中, 总体是指( )
A. 400名学生 B. 被抽取的50名学生
C. 400名学生的体重 D. 被抽取的50名学生的体重
2、下列多项式中，不能用平方差公式分解的是（ ）
A.x2-y2 B.-x2-y2 C.4x2-y2 D.-4+x2
3、不等式
的正整数解有（ ）
A.2个 B.3个 C.4个 D.5个
4、不等式组
的解集为（ ）
A.
≤x≤4 B.＜x≤4 C.＜x＜4 D.≤x＜4
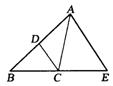
5、如图，A、B两点被池塘隔开，在AB外任选一点C，连结AC、BC分别取其三等分点M、N量得 MN＝38m．则AB的长是
A. 152m
B.114m C.76m D.104m
(第5题图) (第8题图)
6、下列各式从左到右的变形不正确的是（ ）
A.
B
.
C.
D.
7、已知△ABC中，∠ABC与∠ACB的平分线交于O，则∠BOC一定（ ）
A.小于直角 B.等于直角 C.大于直角 D.大于或等于直角
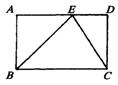
8、如图，在矩形ABCD中，点E是AD上任意一点，则有 （ ）
A．△ABE的周长△CDE的周长＝△BCE的周长
B．△ABE的面积＋△CDE的面积＝△BCE的面积
C．△ABE∽△DEC
D．△ABE∽△EBC
9、化简
的结果是（ ）
A.
B.
C.
D.
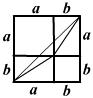
10、观察图形，判断
(a2+b2)与2
的大小（ ）
A.(a2+b2)＞2
B.(a2+b2)＜2
C.(a2+b2)≤2
D.(a2+b2)≥2
二、填空题(每小题3分，共24分)
11、分解因式：
＝
12、化简：
＝
13、如图，CD平分∠ACB，AE∥DC交BC的延长线于点E，若∠ACE＝80°，则∠CAE＝ 度．
 | |||||
 | |||||
 | |||||
(第10题图) (第13题图) (第15题图)
14、已知关于x的不等式组
无解，则a的取值范围是________．
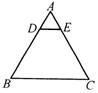
15、如图，在等边三角形ABC中，点D、E分别在AB、AC边上，且DE∥BC．如果BC＝8 cm，AD∶AB＝1∶4，那么△ADE的周长等于________ cm．
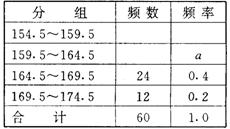
16、为了让学生适应体育测试中新的要求某学校抽查了部分初二男生的身高(注：身高取整数)．经过整理和分析，估计出该校初二男生中身高在160cm以上（包括160cm）的约占80％．右边为整理和分析时制成的频率分布表，其中a＝
。
17、某次数学测验满分为100（单位：分），某班的平均成绩为75，方差为10．若把每位同学的成绩按满分120进行换算，则换算后的平均成绩与方差分别是 ．
18、在一次“人与自然”知识竞赛中，竞赛试题共有25道题．每道题都给出4个答案，其中只有一个答案正确．要求学生把正确答案选出来．每道题选对得4分，不选或选错倒扣2分．如果一个学生在本次竞赛中的得分不低于60分，那么，他至少选对了___________道题．
三、解答题(每小题6分，共12分)
19、计算：
20、解方程：
四、(每小题8分，共16分)
21、有若干个舞蹈演员在舞台上排成一排跳舞，面对观众作队形排列变化，其变化规律是：
一个舞蹈演员A1跳舞，面对观众作队形排列变化的种数是A1为1种；
二个舞蹈演员A1、A2跳舞，面对观众作队形排列变化的种数是A1A2 ；A2A1为2种即1×2种；
三个舞蹈演员A1、A2、A3跳舞，面对观众作队形排列变化的种数是A1A2A3 ，A1 A3A2 ；A2A1A3 ，A2 A3 A1；A3A1A2 ，A3 A2A1为6种即1×2×3种；
请你推测：
(1) 四个舞蹈演员A1、A2、A3、A4跳舞，面对观众作队形排列变化的种数是__ 种；
(2)六个舞蹈演员跳舞，按上述方法作队形排列变化的种数为（用科学记数法表示）_____ 种；
22、条河的两岸有一段是平行的．在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆．在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽．
 |
五、(每小题8分，共16分)
23、根据卫生部2003年对5月21日至5月26日我国内地非典型肺炎疫情的通报，整理列表如下：（单位：人）
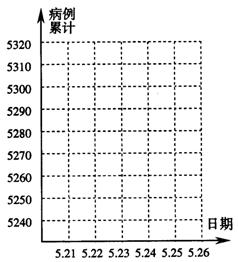
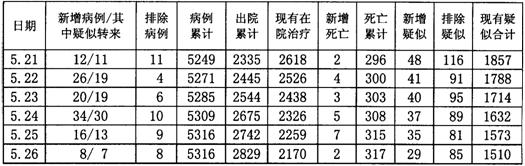
阅读图表，根据要求回答下列问题：
（1）出院累计人数和现有在院治疗人数这两组数据说明了什么问题？
（2）请把表中每天的病例累计人数在下图中用点描出并用折线顺次连结，从中你得到什么结论？
（3）从表中可以看出：今日病例累计＝昨日病例累计＋今日新增病例－今日排除病例．请仿照归纳今日现有疑似合计分别与表中哪几项有关？并用公式的形式写出，然后加以验证．
24、烟台大樱桃闻名全国，今年又喜获丰收，某大型超市从大樱桃生产基地购进一批大樱桃，运输过程中质量损失5％．（超市不负责其它费用）
（1） 如果超市把售价在进价的基础上提高5％，超市是否亏本？通过计算说明．
（2）如果超市要获得至少20％的利润，那么大樱桃售价最低应提高百分之几？（结果精确到0.1%）