河北课改区初中毕业生学业考试数学试卷-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷试题下载

2004年河北省课程改革实验区初中毕业生学业考试

数学试卷

本试卷分卷Ⅰ和卷Ⅱ两部分；卷Ⅰ为选择题，卷Ⅱ为非选择题.

本试卷满分为110分，考试时间为120分钟.

卷Ⅰ（选择题，共20分）

请注意：1. 答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上，考试结束，监考人员将试卷和答题卡一并收回.

　　　　2. 每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.

一、选择题（本大题共10个小题；每小题2分，共20分.在每小题给出的四个选项中，只

有一项是符合题目要求的）

1.　的值是

A．　　　　　　　 B．　　　　　　　 C．　　　　　　　 D．

2.　　　图1中几何体的主视图是

3.　下列计算中，正确的是

A．2a+3b=5ab　　　　　　　　　B．aa³=a³　　　　　　

C．a⁶÷a²=a³　　　　　　　　　 D．(-ab)²=a²b²

4. 第五次全国人口普查结果显示，我国的总人口已达到1 300 000 000人，用科学记数法表

示这个数，结果正确的是

A．1.3×10⁸　　　　　 B．1.3×10⁹　　　　 C．0.13×10¹⁰　　　　 D．13×10⁹

5.　　　如图2，天平右盘中的每个砝码的质量都是1g，则物体A

的质量m(g)的取值范围，在数轴上可表示为

6.　图3是一个经过改造的台球桌面的示意图，图中四个角上的阴影

部分分别表示四个入球孔.如果一个球按图中所示的方向被击出

（球可以经过多反射），那么该球最后将落入的球袋是

A．1 号袋　　　　　　　 B．2 号袋　　　　　

C．3 号袋　　　　　　　 D．4 号袋

7. 小明把自己一周的支出情况，用图4所示的统计图来表示，下面说法正确的是

A．从图中可以直接看出具体消费数额

B．从图中可以直接看出总消费数额　　　　　

C．从图中可以直接看出各项消费数额占总消费额的百分比

D．从图中可以直接看出各项消费数额在一周中的具体变化情况

8.　　　把一个小球以20m/s的速度竖直向上弹出，它在空中的高度h(m)

与时间t(s)满足关系：h=20t-5t².当h=20时，小球的运动时间为

A．20s　　　　　　　　　 B．2s　　　　　　

C．　　　　　 D．

9.　　　如图5，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA=4，

OA=3，则cos∠APO的值为

A．　　　　　　　 B．　　　　　　

C．　　　　　　　 D．

10.　在同一直角坐标系中，函数y=kx-k与(k≠0)的图像大致是

2004年河北省课程改革实验区初中毕业生学业考试

数学试卷

卷Ⅱ（非选择题，共90分）

注意事项：1. 答卷Ⅱ前，将密封线左侧的项目填写清楚.

　　　　 2. 答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.

题号	二	三
题号	二	16	17	18	19	20	21	22	23	24	25
得分

二、填空题（本大题共5个小题；每小题2分，共10分.把答案写在题中横线上）

11.　(-3)²-1=　　　　 .

12. 函数的自变量x的取值范围是　　　　 .

13.　　　图6是根据某市1999年至2003年工业生产总值绘

制的折线统计图.观察统计图可得：增长幅度最大的

年份是　　　　年，比它的前一年增加　　　　亿元.

14.　　　图7是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽

的纸的面积为　　　　 cm²(π取3.14).

15. 扑克牌游戏

小明背对小亮，让小亮按下列四个步骤操作：

第一步分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌现有的张数相同；

第二步从左边一堆拿出两张，放入中间一堆；

第三步从右边一堆拿出一张，放入中间一堆；

第四步左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.

这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是　　　　 .

三、解答题（本大题共10个小题；共80分）

试试基本功

16. （本小题满分6分）

当时，求的值.

17. （本小题满分6分）

已知，如图8，AB和DE是直立在地面上的两根立柱.AB=5m，某一时刻AB在阳光下的投影BC=3m.

（1）请你在图8中画出此时DE在阳光下的投影；

（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长.

归纳与猜想

18. （本小题满分6分）

观察下面的点阵图和相应的等式，探究其中的规律：

（1）在④和⑤后面的横线上分别写出相应的等式；

（2）通过猜想写出与第n个点阵相对应的等式.

19.　（本小题满分8分）

图9是某汽车行驶的路程S(km)与时间t(min)

的函数关系图.观察图中所提供的信息，解答下列问题：

（1）汽车在前9分钟内的平均速度是多少？

（2）汽车在中途停了多长时间？

（3）当16≤t≤30时，求S与t的函数关系式.

判断与决策

20.　（本小题满分8分）

依据闯关游戏规则，请你探究“闯关游戏”的奥秘：

（1）用列表的方法表示有可能的闯关情况；

（2）求出闯关成功的概率.

21.　（本小题满分8分）

在某旅游景区上山的一条小路上，有一些断断续续的台

阶.图11是其中的甲、乙段台阶路的示意图.

请你用所学过的有关统计知识（平均数、中位数、方差

和极差）回答下列问题：

（1）两段台阶路有哪些相同点和不同点？

（2）哪段台阶路走起来更舒服？为什么？

（3）为方便游客行走，需要重新整修上山的小路.对于

　　这两段台阶路，在台阶数不娈的情况下，请你提出

　　合理的整修建议.

操作与探究

22.　（本小题满分8分）

　探索下列问题：

（1）在图12—1给出的四个正方形中，各画出一

　　条直线（依次是：水平方向的直线、竖直方

向的直线、与水平方向成45°角的直线和

　　　　任意的直线），将每个正方形都分割成面积

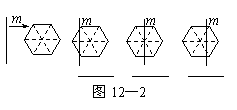　相等的两部分；

（2）一条竖直方向的直线m以及任意的直线n，

在由左向右平移的过程中，将正六边形分成

左右两部分，其面积分别记为S₁和S₂.

①请你在图12—2中相应图形下方的横线上

分别填写S₁与S₂的数量关系式（用“<”，

“=”，“>”连接）；

②请你在图12—3中分别画出反映S₁与S₂

三种大小关系的直线n，并在相应图形下

方的横线上分别填写S₁与S₂的数量关系

式（用“<”，“=”，“>”连接）.

（3）是否存在一条直线，将一个任意的平面图

形（如图12—4）分割成面积相等的两部

分，请简略说出理由.

实验与推理

23.　（本小题满分8分）

用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合，使三角尺的60°角的顶点与点A重合，两边分别与AB，AC重合.将三角尺绕点A按逆时针方向旋转.

（1）当三角尺的两边分别与菱形的两边BC，CD相交于点E，F时，（如图13—1），通过观察或测量BE，CF的长度，你能得出什么结论？并证明你的结论；

（2）当三角尺的两边分别与菱形的两边BC，CD的延长线相交于点E，F时（如图13—2），你在（1）中得到的结论还成立吗？简要说明理由.

综合与应用

24.　（本小题满分10分）

如图14—1是某段河床横断面的示意图.查阅该

河段的水文资料，得到下表中的数据：

x/m	5	10	20	30	40	50
y/m	0.125	0.5	2	4.5	8	12.5

　（1）请你以上表中的各对数据（x，y）作为点的坐标，

　　　　尝试在图14—2所示的坐标系中画出y关于x的

　　　　函数图像；

（2）①填写下表：

x	5	10	20	30	40	50

　　　　 ②根据所填表中数据呈现的规律，猜想出用x表示y

的二次函数的表达式：　　　　　　 .

　　（3）当水面宽度为36米时，一艘吃水深度（船底部到水面的距离）为1.8米的货船能

否在这个河段安全通过？为什么？

25.　（本小题满分12分）

如图15—1和15—2，在20×20的等距网格（每格的宽和高均是1个单位长）中，

Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速

度先向下平移，当BC边与网的底部重合时，继续同样的速度向右

平移，当点C与点P重合时，Rt△ABC停止移动.设运动时间

为x秒，△QAC的面积为y.

（1）如图15—1，当Rt△ABC向下平移到Rt△A₁B₁C₁的位置时，

请你在网格中画出Rt△A₁B₁C₁关于直线QN成轴对称的图形；

（2）如图15—2，在Rt△ABC向下平移的过程中，请你求出y与

x的函数关系式，并说明当x分别取何值时，y取得最大值和

最小值？最大值和最小值分别是多少？

（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，y

取得最大值和最小值？最大值和最值分别是多少？为什么？

（说明：在（3）中，将视你解答方法的创新程度，给予1~4分的加分）

2004年河北省课程改革实验区初中毕业生学业考试

数学试题参考答案及评分标准

说明：

1.　各地阅卷过程中,如考生还有其它正确解法,可参照评分标准步骤酌情给分.

2. 坚持每题评阅到底的原则，当考生的解答在某一步出现错误,影响了后继部分时，如果该

　 步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的给分，但不

　超过后继部分给分数的一半；如果这一步后面的解答有较严重的错误,就不给分.

3. 解答右端所注分数,表示正确做到这一步应得的累加分数.只给整数分数.

4. 对于25（3）题加分的说明：（1）按评分标准给予相应的加分；（2）加分后不超过110

　分的按照“原得分+加分=总分”计算考生的总分.加分后超过110分的，按照110分登

　记总分.

一、选择题（每小题2分，共10分）

题号	1	2	3	4	5	6	7	8	9	10
答案	C	D	D	B	A	B	C	B	C	D

二、填空题（每小题2分，共20分）

11. 8；12. ；13. 2003，40； 14. 942；15. 5.

三、解答题（本大题10个小题，共80分）

16. 解：原式　　 ………………4分

原式=　　　 ………………………4分

17. 解：（1）

　　　　　　　　　　　　　　　　　　　　　　　……………………………………2分

（连接AC，过点D作DE//AC，交直线BC于点F，线段EF即为DE的投影）

（2）∵AC//DF，∴∠ACB=∠DFE.

∵∠ABC=∠DEF=90°∴△ABC∽△DEF.　　　　…………………………4分

∴DE=10（m）.　　　　　 ……………………………………………………6分

　　　说明：画图时，不要求学生做文字说明，只要画出两条平行线AC和DF，再连结EF即可.

18. 答：（1）④1+3+5+7=4²；⑤1+3+5+7+9=5².　　　……………………………………4分

　　　（2）1+3+5+…+(2n-1)=n²　　　　　………………………………………………6分

19. 解：（1）由图像可知：当t=9时，S=12，

　　　　∴汽车在9分钟内的平均速度；……2分

　　　（2）汽车在中途停了7分钟；　……………………………………………………4分

　　　（3）当16≤t≤30时，设S与t的函数关系式为S=kt+b.

　　　　　由图像可知：直线S=kt+b经过点（16，12）和点（30，40），

　　　　　　解得　 …………………………………………7分

　　　　∴S与t的函数关系式为S=2t-20.阶段 ……………………………………………8分

20. 解：（1）所有可能的闯关情况列表表示如下：

	1	2
1	（1，1）	（1，2）
2	（2，1）	（2，2）

…………………………4分
（2）设两个1号按钮各控制一个灯泡，

　　 P（闯关成功）=　　　　　　　　　　 …………………………………………6分

21. （1）

　　　　∴相同点：两段台阶路高度的平均数相同.　……………………………………2分

　　　　不同点：两段台阶路高度的中位数、方差和极差均不相同.　………………4分

（2）甲路段走起来更舒服一些，因为它的台阶高度的方差小. ……………………6分

（3）每个台阶高度均为15cm（原平均数），使得方差为0.　 ……………………8分

22. （1）

（2）①　　　　　　　　　　　　 ……………………………………………………2分

　　　　 ②

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ………………………………………………………6分

（3）存在.

对于任意一条直线l ,在直线l从平面图形的一侧向另一侧平移的过程中，当图形被直线l分割后，设直线l两侧图形的面积分别为S₁，S₂.两侧图形的面积由S₁<S₂（或S₁>S₂）的情形，逐渐变为S₁>S₂（或S₁<S₂）的情形，在这个平移过程中，一定会存在S₁=S₂的时刻.因此，一定存在一条直线，将一个任意平面图形分割成面积相等的两部分.　　 ……………………………………………………………………8分