初中升学数学样卷
一.填空题:(每小题3分,共30分)
1.计算:![]() ;
;
2.2003年5月19日,国家邮政局特别发行“万众一心,抗击‘非典’”邮票,收入全部捐赠给卫生部门,用以支持抗击“非典”斗争,其邮票发行量为枚,用科学记数法表示正确的是 ;
3.分解因式:![]() ;
;
4.函数![]() 的自变量
的自变量![]() 的取值范围是
;
的取值范围是
;
5.用一张圆形的纸片剪一个边长为4cm的正六边形,则这个圆形纸片的半径最小应为
cm;
6.为了调查某一路口某时段的汽车流量,记录了15天同一时段通过该路口的汽车辆数,其中有2天是142辆,2天是145辆,6天是156辆,5天是157辆.那么这15天在该时段通过该路口的汽车平均辆数为 ;
 7.扇形的圆心角为600,弧长为10
7.扇形的圆心角为600,弧长为10![]() ,则这个扇形的面积为 ;
,则这个扇形的面积为 ;
8.已知抛物线![]() 与
与![]() 轴交点的横坐标是-1,则
轴交点的横坐标是-1,则
![]() = _________;
= _________;
9.如图,在△ABC中,∠C=90°,AB=10,AC=8,以AC为
直径作圆与斜边交于点P,则BP的长为 .
10、为了增强公民的节水意识,某制定了如下用水收费标准:每户每月的用水超过10吨时,水价为每吨1.2元,超过10吨时,超过的部分按每吨1.8元收费,该市某户居民5月份用水![]() 吨(
吨(![]() >10),应交水费
>10),应交水费![]() 元,则
元,则![]() 关于
关于![]() 的函数关系式是__________;
的函数关系式是__________;
二.选择题:(每小题4分,共24分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
11。下列各式中,正确的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.已知两圆的半径分别为2、5,而圆心距是一元二次方程![]() 的根,则两圆公切线的条数为
的根,则两圆公切线的条数为
(A) 一条 (B) 三条 (C) 四条 (D) 一条或三条
13.某商店有两个进价不同的计算器都都卖了64 元,其中一个盈利60 %,另一个亏本20 %,在这次买卖中,这家商店
A 不赔不赚 B 赚了8元 C 赔了8元 D 赚了32元
 14.如图:矩形花园ABCD中,
14.如图:矩形花园ABCD中,![]() ,
,![]() ,花园
,花园
中建有一条矩形道路LMPQ 及一条平行四边形道路RSTK。
若![]() ,则花园中可绿化部分的面积为
,则花园中可绿化部分的面积为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
 15.图是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系?
15.图是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度h和时间t之间的关系?
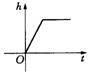

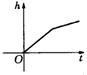

(A)
(B) (C)
(D)
 16.如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内
16.如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内
分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面
上的两数互为相反数,则填在A、B、C内的三个数依次是
(A)0,-2,1(B)0,1,-2(C)1,0,-2(D)-2,0,1
三.解答题:
17.(7分)计算:![]()
18.(8分)先化简,后求值:已知![]() ,其中
,其中![]() ;
;
19.(8分)某机械化养鸡场有一批同时开始饲养的良种鸡1000只,任取10只,称得其质量情况表如下:
![]()
求:(1)这10只鸡的平均质量为多少kg?
(2)考虑到经济效益,该养鸡场规定质量在2.2kg以上(包括2.2kg)的鸡才可以出售,请估计这批鸡中有多少只可以出售?
20.(9分)2003年我国政府工作报告指出:为解决农民负担过重问题,在近两年的税费改革中,我国政府采取了一系列政策措施。2001年中央财政用于支持这项改革试点的资金约为180亿元,预计2003年将达到304.2亿元。求2001年到2003年中央财政每年投人支持这项改革资金的平均增长率。(参考数据:![]() =1.2,
=1.2,![]() =1.3)
=1.3)
21.(10分)已知:如图,四边形ABCD是平行四边形,对角线BD的垂直平分线分别交两边AD,BC于点E、F。
(1)在下图中,根据题意把图形画完整,并标上字母;(2)求证:四边BFDE是菱形。

22.(12分)如图,在直角坐标系中,直线![]() 与双曲线
与双曲线![]() 在第一象限交于点A,与
在第一象限交于点A,与![]() 轴交于点C,AB⊥
轴交于点C,AB⊥![]() 轴,垂足为B,且
轴,垂足为B,且![]() ;(1)求
;(1)求![]() 的值;(2)求⊿ABC的面积;
的值;(2)求⊿ABC的面积;

23. (9分)台湾“华航”客机失事后,祖国大陆海上搜救中心立即通知位于A、B两处的上海救捞人局所属专业救助轮“华意”轮、“沪救12”轮前往出事地点协助搜索。接到通知后,“华意”轮测得出事地点C在A的南偏东60°、“沪救12”轮测得出事地点C在B的南偏东30°。已知B在A的正东方向,且相距100浬,分别求出两艘船到达出事地点C的距离。
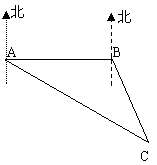 |
24.(12分)如图,⊙O1与⊙O2相交于点A、B,O1 O2分别交⊙O1、⊙O2于点Q、P,过点A的直线EF分别交⊙O1、⊙O2于点E、F,C、D分别是弦AE、AF的中点,M是O1 O2的中点,MA⊥EF,O1A⊥O2A,且O1C、O2D的长是关于![]() 的方程
的方程![]() 的两个根。
的两个根。
⑴求证:AE=AF;
⑵求EF的长;
⑶当![]() 时,求
时,求![]() 的值。
的值。

25.(12分)华联商场以每件30元购进一种商品,试销中发现每天的销售量![]() (件)与每件的销售价
(件)与每件的销售价![]() (元)满足一次函数
(元)满足一次函数![]() ;
;
(1)写出商场每天的销售利润![]() (元)与每件的销售价
(元)与每件的销售价![]() (元)的函数关系式;
(元)的函数关系式;
(2)如果商场要想获得最大利润,每件商品的销售价定为多少为最合适?最大销售利润为多少?
26.(9分)已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE切⊙O于点D,交BC于点E。
(1) 求证:DE⊥BC
(2) 如果CD=4,CE=3,求⊙O的半径。
(3)
求![]() 的值;
的值;
 |
