初三数学总复习教案（六）
三角形（一）
一、知识要点
1、
三角形
ⅰ)三角形的角平分线、中线、高线为三种重要线段，理解
①三角形有关概念及性质 其性质并会画出内心、外心、垂心、重心
ⅱ)三角形三边关系：任意两边之和大于第三边，两边之差小于第三边
a、内角和180˚
ⅲ)三角形中角的关系 b、外角等于与它不相邻两内角和
c、外角大于任一不相邻内角
iv)面积公式
按边分 不等边三角形
等腰三角形 只有两边相等
三边都相等(等边三角形)
②三角形的分类 掌握其判定、性质
锐角三角形
斜角三角形
按角分 钝角三角形
直角三角形 a、合30˚角直角三角形性质
b、直角三角形斜边上中线性质
c、勾股(逆)定理
③全等三角形
ⅰ)了解全等有关概念、性质 以 定义
ⅱ)熟练掌握全等三角形的判定方法 SAS
ASA
AAS （AAS）
SSS
HL(只用于Rt∆)
ⅲ)熟练掌握全等三角形的性质：对应角等，对应线段(边、角平分线、中线、高)相等
ⅳ)命题、定理、逆命题、逆定理有关概念
2、 基本作图(尺规作图)
二、 例题分析
例1、 在∆ABC中，BC=2 AC=7 周长为奇数，求AB的长。
分析：由三角形任意两边之和大于第三边，两边之差小于第三边，可求出AB的范围，再求周长为奇数可确定AB的值。
解：∵BC=2 AC=7
∴7-2＜AB＜7+2 即5＜AB＜9 ∴AB=6、7、8
又∵周长为奇数
∴AB+ BC+ AC= AB+2+7= AB+9为奇数
∴AB=6或8
题后反思：利用三角形三边关系可以解决的问题①任意给出的三条线段能否构成三角形；②利用勾股逆定理，判定是否为Rt∆；③已知两边，可求出第三边的取值范围，再利用其它条件，可确定第三边的取值。
例2、在∆ABC 中，∠A=50˚
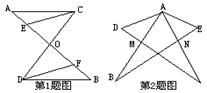
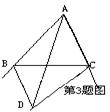
(1) 如图(1) ∆ABC的两条高BD、CE交于O点，求∠BOC的度数
(2) 如图(2) ∆ABC的两条角平分线BM、CN交于P，求∠BPC的度数
A
A
E
N M
D P
O 1 2
B 1 2 C B C
(1) (2)
分析：(1)题中，由高可知有直角，由直角三角形两锐角互余及三角形内角和定理可求得
∠BOC，亦可用四边形内角和去求。
(2)题中，由角平分线定义及三角形内角和定理可求得∠BPC
解：(1)法一：∵BD为∆ABC的高
∴∠BDC=90˚
∴∠1=90˚-∠BCA 同理∠2=90˚-∠ABC
∵∠ABC+AC=180˚-50˚=130˚
∴∠BOC=180˚-(∠1+∠2)
=180˚-(90˚-∠ABC+90˚-∠ACB)
=180˚-180˚+∠ABC+∠ACB=130˚
方法二 ∵BD︰CE为△ABC的高
∴∠BDA=∠CEA=90˚
∵∠A=50˚
∴在四边形AEOD中∠DOE＝360˚－（90˚+90˚+50˚）＝130˚
∴∠BOC＝∠DOE＝130
（2）∵BM CN分别为△ABC的角平分线
∴∠1＝
∠ABC ∠2=∠ACB
∵∠A=50˚
∴∠ABC+∠ACB=180˚-50˚=130˚
∴∠BPC=180˚-(∠1+∠2)
=180˚-(∠ABC+∠ACB)
=180˚-(∠ABC+∠ACB)
=180˚-×130˚
=115˚
题后反思：凡是求角度的题，一般都离不开三角形（多边形）内角和定理及，设法利用这些去推出等量关系。题中应设及到高线，别忘了两锐角互余，遇到角平分线要合理利用其倍分关系。
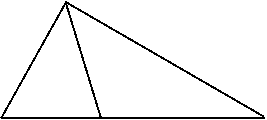
例3、如图△ABC中，AD平分∠BAC，AB+BD＝AC求∠B︰∠C的值
A
B D C
分析：欲求∠B︰∠C的值，直接支求显然不易，我们可以从AB+BD＝AC的突，破点线段的和问题，往往用截长法，或补短法解决通过截长或补短可得到等量线段，再利用等边对等角去处理此问题。
解法一：（截长法）：在AC上截取AE＝AB连接DE
∵AD平分∠BAC
∴∠1＝∠2
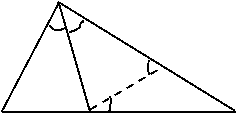在△ABD和△AED中
A
AB＝AE
∠1＝∠2 1 2
AD＝AD 4
∴△ABD≌△AED（SAS）
∴BD＝DE ∠4＝∠B B 3 C
∵AC＝AB+BD 且AE＝AB D
∴EC＝BD
∴DE＝EC
∴∠3＝∠C
∴∠4＝∠3＋∠C＝2∠C
∴∠B＝2∠C
∴∠B︰∠C＝2︰1
解法二：（补短法）延长AB经E，使BE＝BD，连接DE
∴∠E＝∠3
∵AC＝AB+BD
∵AC＝AB＋BE＝AE
A
∵AC平分∠BAC
∵∠1＝∠2 1 2
在△ADE和△ADC中
AE＝AC
B
C
∠1＝∠2 3 D
AD＝AD
∴△ADE≌△ADC（SAS）
∴∠E＝∠C
∵∠ABC＝∠E＋∠3＝2∠E E
∵∠ABC＝2∠E
∴∠B︰∠C＝2︰1
题后反思：此题实际上代表一类题，在利用（或证明）诸如一条线段a等于两线段b、c和对（或a-b=c可能a为a=b+c）通常采用上述两种方法：所增截长法，就是在线段a上截取一段等于b（或c）然后证明余下的一段等于c(或b)；所谓补短法，就是延长线段b（或c使延长部分等于c（或b），再证明它们的和等于a。此题应改为‘在△ABC中，AD平分∠BAC且∠B︰∠C＝2︰1。求证AB+BD＝AC。’证明基本相似，同学们不妨试一试。
课堂练习：
1.已知：如图，AB、CD相交于点O，AC∥DB，OC=OD，E、F为AB上两点，且AE=BF，求证：CE=DF
2.已知：如图，AB=AC，AD=AE，AB、DC相交于点M，AC、BE相交于点N，∠DAB=∠EAC 求证：AM=AN
3.如图，在△ABC中，两外角的平分线BD、CD相交于D，求证：AD平分∠BAC。
