2004年上海市民办中学“八校联考” 2004.3.18　 8:00~10:00

数学试卷（满分120分）

一、填空题：（本大题共14题，每小题2分，满分28分）

1、计算：x¹⁰÷x⁵=　　　　　

2、4³的平方根是　　　　　 

3、上海市现有人口约一千六百三十万左右，用科学记数法表示是　　　　　　　

4、函数的定义域是　　　　　　　

5、方程的解是　　　　　　　 

6、抛物线y=-4x²+3x+2 的对称轴是　　　　　 

7、已知x为实数，且满足(2x²+3x)²+2(2x²+3x)-15=0,则2x²+3x的值为_________

8、小王将5000元存入银行，已知银行一年期利率为x%，一年后，小王将所得的本利和又续存了一年，这样，小王共可得本利和（用含x的代数式表示）

　 　　　　　　　　　　　　　　　

9、已知x₁,x₂,…,x_n的方差为2，则3x₁+5,3x₂+5,…,3x_n+5的标准差为　　　　

10、已知△ABC∽△DEF，且相似比为3∶4，S_△ABC=2cm²,则S_△DEF=　　　　　 cm²。

11、如图，Rt△ABC中，∠C=90°，CD⊥AB于D，BC=，

　　AC=3，则BD=　　　

12、某人沿一斜坡走了5米，升高了2.5米，则此斜坡的坡度为　　　　 

13、平面直角坐标系内，O为坐标原点，A（3，0），B（0，4），将△AOB绕A点逆

时针旋转90°后，将点B转至B′，则点B′的坐标为　　　　　　　　 

14、请设计一个二元二次方程组，使得这个二元二次方程组的解是和 试写出符合要求的方程组　　　　　　　　　　　　 

二、多项选择题：（本大题共4题，每题3分，满分12分）

（每题列出的答案中，至少有一个是正确的，错选或不选得0分，否则

 每漏选1个扣1分，直至扣完为止。）

15、已知，若设，则原方程可化成整式方程_______

　　（A）（B）（C）（D）

16、对二次三项式4x²-6xy-3y²分解因式不正确的是　　　　 

　（A）（B）

　（C）（D）

17、正方形ABCD中，AB=1，分别以A、C为圆心作两个半径为R、r（R>r）的

圆，当R、r满足条件　　　　　　　　　　 时，⊙A与⊙C有2个交点。

　（A）R+r> （B）R-r<< R+r （C）R-r>　（D）0<R-r<

18、以下说法正确的是　　　　

（A）　 每个内角都是120°的六边形一定是正六边形

（B）正n边形有n条对称轴

（C）正n边形的每一个外角度数等于它的中心角度数

（D）正多边形一定既是轴对称图形，又是中心对称图形

三、（本大题共4题，每题7分，满分28分）

19、计算：

20、解方程：3x²+15x+2=2

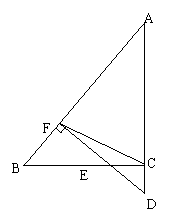
21、如图，△ABC中，∠C=90°，∠A=45°，∠EBC=∠DEC=30°，

若AE=6cm，求DC的长。

22、为了调查上海市中学生的身体状况，在甲、乙两所学校中各随意抽取了

　　100名学生，测试引体向上，结果如下表所示：

　　　　  学校甲　　　　　　　　  　　　　　　 　　 学校乙

人数	6	15	44	20	9	6		人数	6	11	51	18	8	6
次数	3	5	8	11	15	20		次数	3	5	8	11	15	20

　（1）甲乙两校被测学生引体向上的平均数分别是：甲校　　　　　 个，

乙校　　　 个。

　（2）若5个以下（含5个）为不合格，则甲乙两校的合格率分别为

　　　 甲校　　　　  乙校　　　　　

　（3）若15个以上（含15个）为优秀，则甲乙两校中优秀率　　　　　

　　　 校较高（填“甲”或“乙”）

　（4）用你所学的统计知识对两所学校学生的身体状况作一个比较。

　　　 你的结论是　　　　　　　　　　　　　　　　　　　　 

四、（本大题共4题，每题10分，满分40分）

23、反比例函数y= 的图象在第一象限的分支上有一点A（3，4），P为

　　x轴正半轴上的一个动点，

　（1）求反比例函数解析式。

　（2）当P在什么位置时，△OPA为直角三角形，求出此时P点的坐标。

24、某公司要改制成股份公司，原来准备每人平均投资入股，正式统计时有

　 10人表示不参加，因此其余每人要多分担1万元，到实际付款时，又有

　 15人决定退出，这样最后余下的每人要再增加2万元，求统计入股之前

　 有多少人准备入股？统计入股前每人应交多少万元？

25、如图，在△ABC中，∠C=90°，sinB=，F是AB上一点，过点F作

DF⊥AB于F，交BC城E，交AC延长线于D，连CF，若S_△BEF=4S_△CDE,

CE=5，　（1）求AC的长　（2）求S_△CEF

26、已知抛物线y=8x²+10x+1

（1）试判断抛物线与x轴交点情况

（2）求此抛物线上一点A（-1，-1）关于对称轴的对称点B的坐标

（3）是否存在一次函数与抛物线只交于B点？若存在，求出符合条件的一

次函数的解析式；若不存在，请说明理由。

五、（本大题只有1题，满分12分。（1）4分 （2）5分 （3）3分）

27、如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，

当CD 转动时，OA固定不动，0°≤∠DOA≤90°，且总有BC∥OA，AB∥CD，

若OA=4，BC与⊙O交于E，连AD，设CE为x，四边形ABCD的面积为y。

　（1）求y关于x的函数解析式，并指出x的取值范围；

（2）当x=2时，求四边形ABCD在圆内的面积与四边形ABCD的面积

　之比；

（3）当x取何值时，四边形ABCD为直角梯形？连EF，此时OCEF变成什

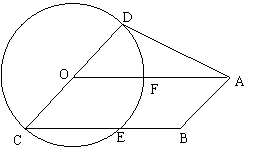　么图形？（只需说明结论，不必证明）。

上海市2004年民办中学初三“八校联考”

数　学　试　卷

（满分120分，考试时间 120分钟）

题号	一	二	三	四	五	总分
得分

一、填空题：（本题共14分，每小题2分，满分28分）

1．计算________。

2．分解因式________。

3．方程的根式是________________。

4．函数的定义域是____________。

5．纳米是长度单位，1纳米等于0.米，用科学记数法表示：

21纳米=_____________米。

6．已知，那么的值是____________。

7．抛物线不过第三象限，则c的取值范围是_________。

8．某学生在一次考试中，语文、数学、英语三门学科的平均成绩是80分，物理、化学两门学科的平均成绩为85分，则该学生这五门学科的平均成绩是_____分。

9．已知点A（a，-2）与点B关于x轴对称，则a+b=________。

10．已知等腰三角形的腰长为4，一腰上的高为2，则其底角的正切值为________________________。

11．如图，正方形木框ABCD，边长为1，四个角用铰链接着，一边BC固定在桌面上，沿AD方向用力推。

正方形变成四边形A′BCD′，

设A′D′交DC于点E，当E

是DC的中点时，两四边形ABCD、A′BCD′重叠部分的面积是__________。

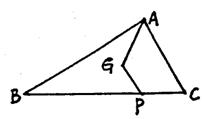
12．如图，G是△ABC的重心，

AG=8，GP∥AC，梯形AGPC的面积

为40，则点C到AG的距离是_________。

13．如图，AD是△ABC的中线，

∠ADC=45°，把△ADB沿AD对折，

点B落在B′的位置，则的值是

__________。

14．观察一组式子，，，，

 ……，请你根据以上规律，写出第6组式子_____________。

二、选择题：（本题共4分，每小题3分，满分12分）

〖在下列各小题中，均给出四个答案，其中至少有一个答案正确，请将正确答案的字母代号填入括号内〗

15．下列各式中与是同类二次根式的是…………………（　　）

（A）　（B）　（C）　（D）

16．△ABC中，AB=AC，一条直线恰好将△ABC分成两个等腰三角形，那么∠BAC度数可能为…………………………………………（　　）

（A）36°　　（B）90°　　（C）108°　　（D）

17．如果两个半径不相等的圆有公共点，那么这两个圆的分切线可能有………………………………………………………………………（　　）

（A）1条　　（B）2条　　（C）3条　　（D）4条

18．下列方程无实根的是…………………………………………（　　）

（A）　　  （B）

（C）　　　　 （D）

三、简答题：（本题共4小题，每小题7分，满分28分）

19．化简，，并求时的值。

20．已知方程　（k﹥0）

（1）求证：方程有两个不相等的实数根。

（2）如果方程的两个根为x₁，x₂，且，求k的值。

　　

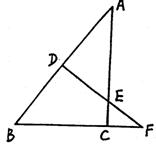21．如图，Rt△ABC中，∠C=90°，DE是AB的垂直平分线，DE分别交AB、AC及BC的延长线于D、E、F，，CE=3。求：的值。

22．从全区6000名考生中抽取100名中学生的数学成绩作为样本，评估毕业生统考数学考试的情况，得到

频率分布直方图，回答下列问题：（每

组可含最低值，不含最高值，60分或

60分以上为及格）

（1）在这100名学生中，人数最

多的一组频率是__________，该组的人

数是_______________；

（2）根据样本估计全区考生数学成绩的及格率为____________；

（3）全区约有______考生的成绩在80分以上。

四、解答题：（本题共有4小题，每小题10分，满分40分）

23．二次函数的图象与x轴交于A、B两点，点A在y轴左侧，点B在y轴右侧，又与y轴交于点C，且AC²+BC²=28。

（1）求函数解析式；

（2）求此抛物线顶点M的坐标及直线MC与x轴的交点N的坐标；

（3）设P为直线AC上的点，且∠CPN=60°。求P点的坐标。

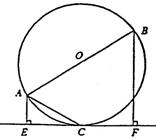24．如图，AB是⊙O的直径，直线EF与⊙O相切于点C，AE⊥EF于E，BF⊥EF于F，连续AC。

（1）求证：AC平分∠BAE；

（2）求证：

25．某厂购进由甲、乙两种原料配成的两种材料，已知材料按甲：乙=5：4配料，每吨50元；另一种材料按甲：乙=3：2配料，每吨48.6元，那么甲、乙两种原料的价格各是多少？

26．如图，一次函数的图象经过第一、三、四象限，且与反比例函数的图象交于点A、B，与X轴、Y轴分别交于点C和点D，且点A的纵坐标值与横坐标值之比为1：5，，△AOD的面积为。求：

（1）反比例函数的解析式；

（2）一次函数的解析式；

（3）在x轴正半轴上是否存

在点E，使△DCE与△ODB相似？

若存在，试求出E点的坐标；若不

存在，请说明理由。

五、（本题12分）

27．已知正方形ABCD的边长为6，以D为圆心，DA为半径在正方形内作AC，E是AB边上动点，（与点A、B不重合）过E作AC切线，交BC于点F，G为切点，⊙O是△EBF的内切圆，切EB、BF、FE于P、J、H。

（1）求证：△ADE∽△PEO；

（2）设AE=x，⊙O 的半径为y。求y关于x的函数关系式，并写出定义域；

（3）当⊙O的半径为1时，求CF的长；

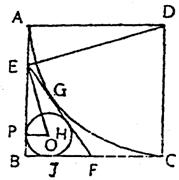（4）当点E在移动时，图中哪些线段与线段EP绐终保持相等长？请说明理由。