绝密 ★ 启用前 试卷类型：A
淄博市中等学校招生考试
数 学 试 题
注意事项：
1.答题前请考生务必在答题卡及试卷的规定位置将自己的姓名、考试号、考试科目、座号等内容填写（涂）准确.
2.本试题分第I卷和第II卷两部分.第I卷（1-4页）为选择题，42分；第II卷（5-12页）为非选择题，78分；共120分.考试时间为120分钟.考生可以使用计算器.
3.第I卷每小题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号（A B C D）涂黑.如需改动，须先用橡皮擦干净，再改涂其它答案.第II卷须用蓝黑钢笔或圆珠笔直接答在试卷上.
4.考试结束后，由监考教师把第I卷和第II卷及答题卡一并收回.
第I卷（选择题 共42分）
一、选择题：本题共12小题，在每小题所给出的四个选项中，只有一个是正确的，请把正确的选项涂在答题卡的相应位置上.第1-6小题每题3分，第7-12小题每题4分.错选、不选或选出的答案超过一个，均记零分.
1.“世界银行全球扶贫大会”于2004年5月26日在上海开幕.从会上获知，我国国民生产总值达到11.69万亿元，人民生活总体上达到小康水平，其中11.69万亿用科学记数法表示应为
（A）11.69×
（B）
（C）
（D）
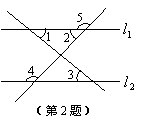2．如图，下列条件中，能判断直线
//
的是
（A）∠2=∠3
（B）∠1=∠3
（C）∠4+∠5=180°
（D）∠2=∠4
３.某项科学研究，以45分钟为1个时间单位，并记每天上午10时为0，10时以前记为负，10时以后记为正，例如9：15记为-1，10：45记为1等等，依此类推，上午7：45应记为
（A）3 （B）-3
（C）-2.15 （D）-7.45
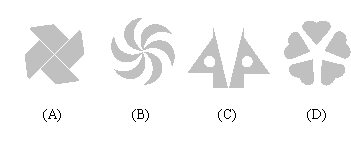４.在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转.下列图案中，不能由一个圆形通过旋转而构成的是
5.用一把带有刻度的直角尺，
①可以画出两条平行的直线
与
，如图（1）；
②可以画出∠AOB的平分线OP，如图（2）；
③可以检验工件的凹面是否成半圆，如图（3）；
④可以量出一个圆的半径，如图（4）.
 |
上述四个方法中，正确的个数是
（A）1个 （B）2个
（C）3个 （D）4个
６.若关于x的一元二次方程
有实数根，则k的取值范围是
（Ａ）k＞－1 （Ｂ）k≥－1
（Ｃ）k＞－1且k≠0 （Ｄ）k≥－1且k≠0
7．化简二次根式
的结果是
（A）
(B)
(C)
(D)
8. 方程
=1的根是
（A）
（B）
（C）
（D）
9. 观察下列数表：
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
4
5
6
7 … 第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为
（Ａ）
（Ｂ）
（Ｃ）
（Ｄ）
10. 如图，∠1＝∠2＝∠3，则图中相似三角形共有
（A）1对 （B）2对
（C）3对 （D）4对
11. 已知函数
经过点
如果
那么
（Ａ）
（Ｂ）
（Ｃ）
（Ｄ）
12. 如图是一块长、宽、高分别是6cm,4cm和3cm的长方体木块.一只蚂蚁要从长方体木块的一个顶点
处，沿着长方体的表面到长方体上和相对的顶点
处吃食物，那么它需要爬行的最短路径的长是
(A) （
）
(B) 
(C) 
(D) 
绝密 ★ 启用前 试卷类型：A
淄博市2004年中等学校招生考试
数 学 试 题
第II卷（非选择题 共78分）
| 得分 | 评卷人 |
二、填空题：本题共5小题，满分20分.只要求填写最后结果，每小题填对得4分.
13. 2004年5月16日是世界第十四个助残日，这天某校教师为本区的特殊教育中心捐款的情况如下表：
| 捐款人数 | 32 | 11 | 9 | 21 | 8 | 4 |
| 捐款金额（元／人） | 20 | 30 | 40 | 50 | 100 | 200 |
该校教师平均每人捐款约 元（精确到１元）.
14．写出一个含有字母
的分式（要求：不论取任何实数，该分式都有意义，且分式的值为负）
．
15. 用一条宽相等的足够长的纸条，打一个结，如图（１）所示，然后轻轻拉紧、压平就可以得到如图（２）所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝ 度.
 | |||
 | |||
16．根据指令[s,A]（s≥0, 0°≤A<360°）机器人在平面上能完成如下动作：先在原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s. 现在机器人在平面直角坐标系的原点，且面对y轴的负方向，为使其移动到点（-3，3），应下的指令是 .
17．过边长为1的正方形的中心O引两条相互垂直的射线，分别与正方形的边交于A，B两点，则线段AB长的取值范围是 .
三、解答题：本题共7小题，共58分.解答应写出文字说明、证明过程或演算步骤 .
| 得分 | 评卷人 |
18.（本题满分5分）
计算：
| 题号 | 得分 | |
| 二 | ||
| 三 | 18 | |
| 19 | ||
| 20 | ||
| 21 | ||
| 22 | ||
| 23 | ||
| 24 | ||
| 总分 | ||
| 座号 |
| 得分 | 评卷人 |
19.（本题满分7分）
根据对全国31个省（区、市）68000个农户的抽样调查，一季度，农民人均现金收入（包括工资性收入、出售农产品收入、生产经营收入和财产性、转移性现金收入）比上年同期有明显增长. 其中三项现金收入人均增长数额占一季度人均现金收入增长数额的百分数如图所示，而出售农产品收入增加最多，达44元.
（数据来源：国家统计局2004-04-27）
请根据以上信息回答下列问题：
（1）一季度农民人均现金收入增加了多少元（精确到1元）？
（2）农民人均生产经营收入增加了多少元（精确到1元）？请在图中相应的位置画出示意图，并标注所占的百分数.
| 得分 | 评卷人 |
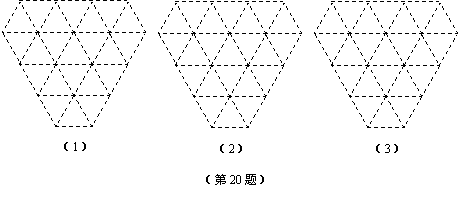
20.（本题满分８分）
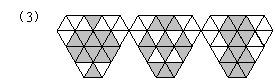
请你在下面3个网格（两相邻格点的距离均为1个单位长度）内，分别设计1个图案，要求:在(1)中所设计的图案是面积等于
的轴对称图形；在（2）中所设计的图案是面积等于2的中心对称图形；在（3）中所设计的图案既是轴对称图形又是中心对称图形，并且面积等于3．将你设计的图案用铅笔涂黑．
 |
| 得分 | 评卷人 |
21.（本题满分8分）
我市一山区学校为部分家远的学生安排住宿，将部分教室改造成若干间住房. 如果每间住5人，那么有12人安排不下；如果每间住8人，那么有一间房还余一些床位，问该校可能有几间住房可以安排学生住宿？住宿的学生可能有多少人？
| 得分 | 评卷人 |
22.（本题满分10分）
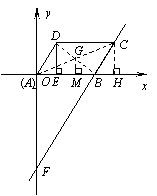
四边形ABCD是平行四边形，AB=3，
,高DE=2. 建立如图所示的平面直角坐标系，其中点A与坐标原点O重合.
（1）求BC边所在直线的解析式；
（2）设点F为直线BC与y轴的交点，求经过点B，D，F的抛物线解析式；
（3）判断□ABCD的对角线的交点G是否在（2）中的抛物线上，并说明理由.
| 得分 | 评卷人 |
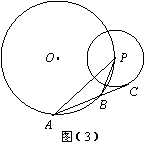
23.（本题满分10分）
已知⊙
的半径为Ｒ，⊙P的半径为r（r<R），
且⊙P的圆心Ｐ在⊙上. 设Ｃ是⊙Ｐ上一点，过
点C与⊙P相切的直线交⊙O于A、B两点.
（1）若点C在线段OP上，（如图1）.
|
求证：PA·PB=2Rr；
（2）若点C不在线段OP上，但在⊙O内部
如图（2）. 此时，（１）中的结论是否成立？若成
|
|
立，请给予证明；若不成立，说明理由；
|
|
求给予证明或说明理由.
 |
|
| 得分 | 评卷人 |
24.（本题满分10分）
在日常生活中，我们经常看到一些窗户上安装着遮阳蓬，如图（1）.现在要为一个面向正南的窗户设计安装一个遮阳蓬，已知该地区冬天正午太阳最低时，光线与水平线的夹角为34°；夏天正午太阳最高时，光线与水平线的夹角为76°.
把图（1）画成图（2），其中AB表示窗户的高，BCD表示直角形遮阳蓬.
（1）遮阳蓬BCD怎样设计，才能正好在冬天正午太阳最低时光线最大限度地射入室内而夏天正午太阳最高时光线刚好不射入室内？请在图（3）中画图表示；
（2）已知AB=150cm，在（1）的条件下，求出BC，CD的长度（精确到1cm）.
   |
试卷类型：A
淄博市2004年中等学校招生考试
数学试题（A卷）参考答案及评分标准
第Ⅰ卷（选择题 共42分）
一、选择题：（第1—6题每题选对得3分，第7—12题每题选对得4分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | B | C | D | D | B | C | A | D | A | C |
第Ⅱ卷（非选择题 共78分）
二、填空题：（只要求填写最后结果，每小题填对得4分）
13. 47; 14. 
(或
,答案不唯一，只要符合要求，均给相应的分数);
15.
36°; 16. 
； 17. 
≤AB≤1.
三、解答题：（本大题共7小题，共58分，解答要写出必要的文字说明、证明过程或演算步骤）
18．(本题满分5分)
解：原式
…………………………………4分
=.…………………………………………………………… 5分
19．(本题满分7分)
解：(1)设一季度农民人均现金收入增加了x元.
由题意，得45.4％·x=44.
………………………1分
解得 x≈97(元).
答：一季度农民人均现金收入增加了97元. ……3分
（2）设农民人均生产经营收入增加了x元，
由题意，得
.
解得 x≈7(元).
答：农民人均生产经营收入增加了7元；…………………… 5分
示意图及所占百分数，如图. ……………………… 7分
20．(本题满分8分)
 |
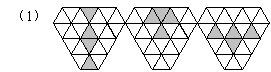…………………………2分
 |
……………………………5分
 |
…………………………8分
说明：以上每题只给出了三种涂法，其它涂法只要符合要求，可给相应的分数.
21．(本题满分8分)
解：设有x间住房，有y名学生住宿.
根据题意，得
……………………3分
把①代入②，得
0
8x-5x-128
解得
. ……………………………………………………… 5分
因为x为整数，所以x可取5，6, …………………………………………6分
把x的值代入①，得y的值为37，42. ………………………………… 7分
| |
22．(本题满分10分)
解：（1）过点C作CH⊥x轴于H. 在Rt△BCH中，BC=AD=
，CH=DE=2.
∴
BH=
又∵ AB=3，∴ AH=AB+BH=4. ∴ B（3，0），C（4，2）。…………… 1分
设BC所在直线的解析式为y=kx+b.
将B（3，0），C（4，2）代入得
解得 k=2, b= －6.
∴ BC边所在直线的解析式为y=2x－6. …………… 3分
(2) 在Rt△ADE中，AE=, ∴D(1,2).
设点F（0，b），代入y=2x-6，得b=－6.
∴ F（0，－6）.……………………………………… 4分
设经过点B，D，F的抛物线为
，
由题意，得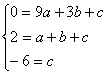
……………………………………………… 5分
解得
.
∴ 抛物线的解析式为
.…………………………………… 6分
(3)□ABCD对角线的交点G不在（2）中的抛物线上.……………………… 7分
连结AC、BD相交于G，过G作GM⊥x轴于M，则GM∥CH∥DE.
∵
AG=GC， ∴ 
，
.
∴点G（2，1）.……………………………………………………………… 8分
把x=2，代入,得
∴点G（2，1）不满足，
即（2）中的抛物线不经过□ABCD的对角线的交点.………………… 10分
23．(本题满分10分)
解： （1）证明：延长PO交⊙O于点Q，
连结AQ，如图（1）.……………………… 1分
∵AB与⊙P相切于点C，且PC是⊙P的半径，
∴AB⊥PC，即∠PCB=90°.
又∵PQ是⊙O的直径，
∴∠PAQ=90°.………………………… 2分
∵∠PQA=∠PBC，
∴Rt△PAQ∽Rt△PCB,
∴
即 PA·PB=PQ·PC.
又∵PQ=2R，PC=r,
∴PA·PB=2Rr.…………………………… 4分
（2）（1）中的结论成立.………………… 5分
证明：连结PO并延长交⊙O于点Q，
连结AQ，PC，如图（2）.……………… 6分
由已知条件，得
∠PAQ=∠PCB=90°.…………………… 7分
又∠PQA=∠PBC，
∴Rt△PAQ∽Rt△PCB，
∴，
即PA·PB=PQ·PC=2Rr.……………… 8分
（3）答：PA·PB=2Rr.……………… 10分
24．(本题满分10分)
解：（1）如图.………………………………………………3分
（2）如图，设BC=x，CD=y.
在Rt△ADC和Rt△DBC中，
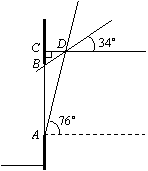
由题意，得 
………7分
把②代入①，得
，
(cm)，
(cm).
答：BC、CD的长度分别约为30cm、45cm。……………10分