初三模拟试卷
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | |||
| 19 | 20 | 21 | 22 | 23 | |||||
| 得分 | |||||||||
一、选择题（每题4分，共48分）
1、
的倒数是（ ）
（A）
（B）
（C）2 （D）-2
2、下列计算正确的是（ ）
（A）
（B）
（C）（-a3 ）2 =a5 （D）a12÷a6=a6
3、据测算，我国每天因土地沙漠化造成的经济损失为1.5亿元，若一年按365天计算，用科学记数法（保留3个有效数字）表示我国一年因土地沙漠化造成的经济损失为（ ）元
（A）5.475×1010 （B）5.48×1010 （C）0.5475×1011 （D）548×108
4、如图，D在AB上，E在AC上，且∠B=∠C，那么补充
下列条件后仍无法判定△ABE≌△ACD的是（ ）
（A）AD=AE （B）∠AEB=∠ADC
（C）BE=CD （D）AB=AC
5、右边是一个可以自由转动的转盘，转动这个转盘，
指针落在蓝色区域的概率是（ ）
（A）
（B）
（C）
（D）
6、底面半径为3㎝，高为4㎝的圆锥的侧面积为（ ）
（A）7.5π㎝2 （B）12π㎝2
（C）13π㎝2 （D）24π㎝2
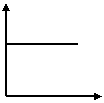
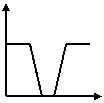
7、一辆公共汽车从车站开出，加速行驶一段后开始匀速行驶。过了一段时间，汽车到达下一个车站。乘客上下车后汽车开始加速，一段时间后又开始匀速行驶。
下面的哪一幅图可以近似地刻画出汽车在这段时间内的速度变化情况？（ ）
速度
速度
速度
速度
时间 时间 时间 时间
（A） （B） （C） （D）
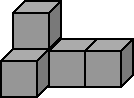8、从不同方向观察同一物体时，可能看到不同的图形。
其中，从正面看到的图叫做主视图，从左面看到的图
叫做左视图，从上面看到的图叫做俯视图。请问，下
面哪一幅图是右面这个几何体的左视图？（ ）
 | |||||||
 |  |  | |||||
（A） （B） （C） （D）
9、在平面直角坐标系中，半径为1和6的两个圆的圆心坐标
分别是（－3，0）和（0，4），则两圆的位置关系是（ ）
（A）相交 （B）内切 （C）外切 （D）外离
10、如图，⊙O中，弦AB与半径OC相交于点M，且
OM=MC，若AM=1.5，BM=4，则OC的长度为（ ）
（A）
（B）
（C）
（D）
11、若一个正多边形的边心距与边长之比为
，则此正多边形是（ ）
（A）正十二边形 （B）正三角形 （C）正六边形 （D）正方形
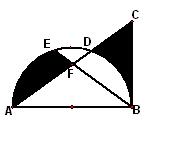12、如图，AB为半圆直径，BC为切线，BE为弦，AC交
半圆于点D，交BE于F点，已知AF=FC，BC=AC=1，
则图中阴影部分的面积为（ ）
（A）
（B） （C）
（D）
二、填空题（每题5分，共30分）
13、因式分解：a2-4b2+4b-1=
14、不等式组
的正整数解是
15、关于x的一元二次方程（k-1）x2-2x+3=0有两个不相等的实数根，则k的取值范围是
16、如图，矩形ABCD中，AB=12，AD=10，将此矩形折叠，
使点B落在AD边的中点处，则折痕FG的长为
17、从甲、乙、丙三人中选取2人去参加运动会有甲和乙、甲和丙、乙和丙3种不同的选法。抽象成数学模型即：从3个元素中选取2个元素的组合，记作 
；一般地，从m个元素中选取n个元素（n≤m）的组合，记作
。根据以上分析从8人中选取5人去参加运动会的不同选法有
种。
18、一堆有红、白两种颜色的球各若干个，已知白球的个数比红球少，但白球个数的2倍比红球多。若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为60，则白球最多有 个
三、解答题（每题8分，共24分）
19、计算：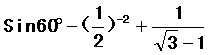
20、解方程组：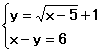
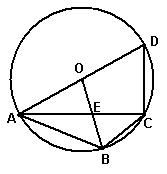21、如图，四边形ABCD内接于⊙O，已知直径AD=2，
∠ABC=120°，∠ACB=45°，连OB交AC于点E。
（1） 求AC的长；
（2） 求CE︰AE的值；
（3） 在CB的延长线上取一点P，使PB=2BC，试判断
直线PA和⊙O的位置关系，并证明你的结论。
四、解答题（共22分）
22、（本题10分）某企业有员工300人，生产A种产品，平均每人每年可创造利润m万元（m为大于零的常数）。为减员增效，决定从中调配x人去生产新开发的B种产品。根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54m万元。
（1）调配后，企业生产A种产品的年利润为 万元，企业生产B种产品的年利润为 万元（用含x和m的代数式表示）。若设调配后企业全年总利润为y万元，则y关于x的函数解析式为 。
（2）若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的
，生产B种产品的年利润大于调配前企业年利润的，应有哪几种调配方案？请设计出来，并指出其中哪种方案全年总利润最大（必要时，运算过程可保留3个有效数字）。
（3）企业决定将“（2）”中的年最大总利润（设m=2）继续投资开发新产品。现有6种产品可供选择（不得重复投资同一种产品），各产品所需资金及所获利润如下表：
| 产 品 | C | D | E | F | G | H |
| 所需资金（万元） | 200 | 348 | 240 | 288 | 240 | 500 |
| 年利润（万元） | 50 | 80 | 20 | 60 | 40 | 85 |
如果你是企业决策者，为使此项投资所获年利润不少于145万元，你可以投资开发哪些产品？请写出两种投资方案。（不写解题过程）
23、（本题12分）如图，直线l与x轴交于点P（1，0），与x轴所夹的
锐角为θ，且tanθ=
，直线l与抛物线
（a＞0）相交于
B（m，－3），D（3，n）
（1） 求B、D两点的坐标，并用含a的代数式表示b和c；
（2） ①若关于x的方程
有实数根，
求此时抛物线的解析式；
②若抛物线（a＞0）与x轴交于A、C两点，顺次连接A、B、C、D得凸四边形ABCD，问四边形ABCD的面积有无最大值或最小值？若有，求出面积的最大值或最小值；若无，请说明理由。
五、画图题（本题12分）
24、为了美化环境，我校在教学前楼的正方形空地上分别种植四种不同的花草，现将这块空地按下列要求分成四块：①分割后的整个图形必须是对称图形；②四块图形形状相同；③四块图形面积相等。现已有两种不同的分法：
（1） 分别作两条对角线（图1）；
（2） 过一条边的四等分点作这边的垂线段（图2）；（图2中两个图形的分割看作同一方法）
请你按照上述三个要求，分别在下面三个正方形中给出另外三种不同的分割方法（只要求正确画图，不写画法）
图1 图2
 | |||
 | |||
方法1 方法2
（轴对称图形） （中心对称图形）
|
方法3
（既是中心对称又是轴对称）
六、解答题（本题14分）
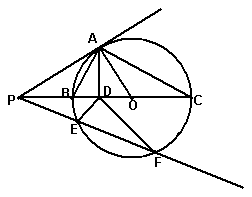
25、 如图，△ABC内接于⊙O，BC是⊙O的直径，
AD⊥BC，D为垂足，BD＜DC，过点A的切
线交直径CB的延长线于点P，过点P任作
⊙O的割线PEF交⊙O于点E、F，已知AB=2，
（1） 求sin∠AOD的值；
（2） 设DE=x，PF=y，求y关于x的函数关系式及自变量x的取值范围。
（3） 试探索是否存在这样的割线PEF，使得DE=EF，如果存在，
求出cos∠OPF的值；如果不存在，请说明理由。