初三数学（上）期末考试试卷

 

班级　　　姓名　　　　 学号　　　成绩　　　　.

 

一、填空题：（每空3分，共42分）

1.　　　 抛物线的对称轴是　　　 ；顶点的坐标是　　　　 ；

2.　　　 已知正比例函数y＝kx与反比例函数的图象都过A（m，1），则m＝　　　 ，正比例函数的解析式是　　　　　 ；

3.　　　 一个植树小组共有6名同学，其中有2人各植树20棵，有3人各植树16棵，有1人植树14棵，平均每人植树　　　　　　　　  ；

4.　　　 一条弦把圆分为2∶3的两部分，那么这条弦所对的圆周角度数为　　　　　  ；

（第8题）　　　　 （第9题）　　　　　　　 （第11题）

			第12题

5.　　　 如果两圆的半径分别为1和2，圆心距为，那么一条外公切线的长是　　　　　 ；

6.　　　 若正多边形的一个内角等于140°，则它是正　　　　　　  边形；

7.　　　 如果半径为5的一条弧的长为，那么这条弧所对的圆心角为　　　　　　  ；

8.　　　 如图，三个半径为r的等圆两两外切，且与△ABC的三边分别相切，则△ABC的边长是　　　　　　　　  ；

9.　　　 某人清晨在公路上跑步，他距某标志牌的距离S（千米）是跑步时间t（小时）的一次函数如图。若该函数的图像是图中的线段BA，该一次函数的解析式是　　　　　　 ；

10.　 与半径为R的定圆O外切，且半径为r的圆的圆心的轨迹是　　　 　　　　　　　　　　　　　　　　　　　 ；

11.　 如图，有两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD经过点P，且CD＝13，PD＝4，两圆组成的圆环的面积是　　　　　　  ；

12.　 统计某校初三年级期中考试数学成绩的频率分布直方图如图所示，从该图可以看出这次考试数学成绩的及格率等于　　　　  。（学生分数都取整数，60分以下为不及格）。

二、选择题：（每题2分，共22分）

13.　 若圆锥的母线长为4cm，底面半径为3cm，则圆锥的侧面展开图的面积是（　　　）
（A）；　　 （B）；　　 （C）；　　 （D）；

14.　 一个正方形的内切圆半径，外接圆半径与这个正方形边长的比为（　　 ）
（A）1∶2∶；　　 （B）1∶∶2；　（C）1∶∶4；　（D）∶2∶4；

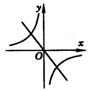
15.　 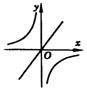函数y＝kx和的图象是（　　  ）




　 （A）　　　　　  （B）　　　　　 （C）　　　　　  （D）

16.　 某部队一位新兵进行射击训练，连续射靶5次，命中的环数分别是0，2，5，2，7。这组数据的中位数与众数分别是（　　　 ）
（A）2，2；　　　 （B）5，2；　　　　  （C）5，7；　　　　　　 （D）2，7；

17.　 若二次函数的图象如图所示，则点（a＋b，ac）在（　　  ）
（A）第一象限；　　 （B）第二象限；　　  （C）第三象限；　　（D）第四象限；

18.　 一个圆锥的底面半径为10，母线长30，则它的侧面展开图（扇形）的圆心角是（　　 ）
（A）60° ；　　 （B）90°；　　 （C）120°；　　　（D）150°；

19.　 如图，⊙O中，弦AD∥BC，DA＝DC，∠AOC＝160°，则∠BCO等于（　　 ）
（A）20°；　 （B）30°；　 （C）40°；　 （D）50°；

（第17题）　　　 （第19题）　　　　（第20题）　　　 （第23题）

20.　 如图，正比例函数与反比例函数的图象相交于A、C两点，过A作x轴的垂线交x轴于B，连结BC，若△ABC面积为S，则（　　 ）
（A）S＝1；　（B）S＝2；　（C）S＝3；　（D）S＝；

21.　 在面积相等的两块田里种植了甲、乙两种水稻，并记录到这两块田在连续10年中的年产量。现在要比较这两种水稻产量的稳定性，为此应（　　　 ）
（A）比较它们的平均产量；（B）比较它们的方差；（C）比较它们的最高产量；（D）比较它们的最低产量；

22.　 同圆的内接正十边形和外切正十边形的周长之比等于（　　 ）
（A）sin18° ；（B）cos18°；（C）sin36°；（D）cos36°；

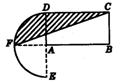
23.　 设计一个商标图案：先作矩形ABCD，使AB＝2BC，AB＝8，再以点A为圆心、AD的长为半径作半圆，交BA的延长线于F，连FC。图中阴影部分就是商标图案，该商标图案的面积等于（　　 ）
（A）4π＋8；（B）4π＋16；（C）3π＋8；（D）3π＋16；

24.　 如图，正比例函数与反比例函数的图象相交于A、C两点，过A作x轴的垂线交x轴于B，连结BC，若△ABC面积为S，则（　　 ）
（A）S＝1；　（B）S＝2；　（C）S＝3；　（D）S＝；

25.　 在面积相等的两块田里种植了甲、乙两种水稻，并记录到这两块田在连续10年中的年产量。现在要比较这两种水稻产量的稳定性，为此应（　　　 ）
（A）比较它们的平均产量；（B）比较它们的方差；（C）比较它们的最高产量；（D）比较它们的最低产量；

26.　 同圆的内接正十边形和外切正十边形的周长之比等于（　　 ）
（A）sin18° ；（B）cos18°；（C）sin36°；（D）cos36°；

27.　 设计一个商标图案：先作矩形ABCD，使AB＝2BC，AB＝8，再以点A为圆心、AD的长为半径作半圆，交BA的延长线于F，连FC。图中阴影部分就是商标图案，该商标图案的面积等于（　 　）
（A）4π＋8；（B）4π＋16；（C）3π＋8；（D）3π＋16；

三、计算题或证明题：

28.　 （本题9分）已知：直线、分别与x轴交于点A、C，且都经过y轴上一点B，又的解析式是y＝－x－3，与x轴正半轴的夹角是60°。
求：⑴直线的函数表达式；　　⑵△ABC的面积；

29.　 （本题9分）已知：如图，⊙O和⊙A相交于C、D，圆心A在⊙O上，过A的直线与CD、⊙A、⊙O分别交于F、E、B。
求证：⑴△AFC∽△ACB； ⑵；

四、综合题：

30.　 （本题9分）已知：如图，在Rt△ABC中，斜边AB＝5厘米，BC＝a厘米，AC＝b厘米，a＞b，且a、b是方程的两根，
⑴求a和b的值；
⑵若△A′B＇C＇与△ABC开始时完全重合，然后让△ABC固定不动，将△A＇B＇C＇’以1厘米/秒的速度沿BC所在的直线向左移动。
　ⅰ)设x秒后△A’B’C’与△ABC 的重叠部分的面积为y平方厘米，求y与x之间的函数关系式,，并写出x的取值范围；

　　ⅱ)几秒后重叠部分的面积等于平方厘米？

31.　 （本题9分）已知抛物线与x轴相交于不同的两点A（,0）,B（，0），（B在A的右边）又抛物线与y轴相交于C点，且满足，
⑴求证：；

⑵问是否存在一个⊙O’，使它经过A、B两点且与y轴相切于C点，若存在，试确定此时抛物线的解析式及圆心O’的坐标，若不存在，请说明理由。