初三数学 解直角三角形的应用
一、选择题：
1．已知等腰三角形底边上的高等于腰的
，则项角为
（ ）
（A） 300 （B） 450 （C） 600 （D） 900
2．菱形ABCD的对角线AC=10，BD=6，则 tan
=
（ ）
（A） 
（B）
（C） 
（D）以上都不对
3．在高出海平面100米的山岩上一点A，看到一艘船B的俯角为300，则船与山脚的水平距离为 （ ）
（A） 50米 （B）200米 （C）100
米 （D）
米
4．正方形的对角线长为，则正方形的面积为
（ ）
（A） 9 （B）
（C）
（D）
5．如果三角形的斜边长为4，一条直角边长为2，那么斜边的高为 （ ）
（A） 2
（B）
（C）
（D）2
6．Rt△ABC中，∠C=900，斜边AB的坡度为1：2，若BCAC，则BC：AC：BA等于 （ ）
（A） 1：2：
（B）1：：2 （C） 1：
（D）1：2：5
7．若从山项A望地面C、D两点的俯角分别为450、300，C、D与山脚B共线，若CD=100米，那么山高AB为 （ ）
（A）
100米
（B） 50米 （C） 50
米 （D）
50（
）米
8．已知△ABC中，AD是高，AD=2，DB=2，CD=2，则∠BAC=
（ ）
(A) 1050 (B) 150 (C) 1050或150 (D) 600
9．已知△ABC中，∠ABC=900，∠ACB=450，D在BC的延长线上，且CD=CA，则cot
的值为
（ ）
（A） 
（B）
（C）
（D）
10．已知：△ABC中，∠BCA=900，CD⊥AB于D，若AD=1，AB=3，那么∠B的余弦值为（ ）
（A） 
（B） 
（C） 
（D）
二、填空题：
1．若地面上的甲看到高山上乙的仰角为200，则乙看到甲的俯角为 度。
2．已知一斜坡的坡度为1：，则斜坡的坡度为
。
3．已知一斜坡的坡度为1：4，水平距离为20米，则该斜坡的垂直高度为 。
4．在山坡上种树，要求株距为5.5米，测得斜坡的倾斜角为300，则斜坡上的相邻两株间的坡面距离是 米。
5.已知直角梯形ABCD中，AB∥CD，∠D=900，AC⊥BC，若AC=3，BC=3，则AB= 。
6．已知锐角△ABC中，AD⊥BC于D，∠B=450，DC=1，且
=3，则AB=
。
7．已知菱形的两条对角线分别是8和8，则菱形的周长为
。
8．已知如图，将两根宽度为2cm的纸带交叉叠放，若∠α为已知，
则阴影部分面积为 。
9．如图所示，某建筑物BC直立于水平地面，AC=9米，要建造阶梯
AB，使每阶高不超过20厘米，则阶梯至少要建 阶。
（最后一阶的高不足20厘米时，按一阶计算；取1.732）
三、解答题：
1． 已知如图，Rt△ABC中，∠ACB=900，D是AB的中点，
sinα=
,AC=
,求 。
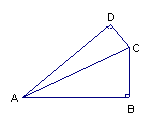2.已知如图：四边形ABCD中，∠B=∠D=900，∠BAD=600，且BC=11，CD=2，求AC的长。
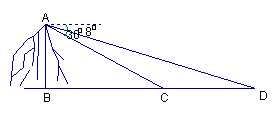
3．我人民解放军在进行“解放一号”军事演习时，于海拔高度为600米的某海岛顶端A处设立了一个观察点（如图）上午九时，观察员发现“红方C舰”和“蓝方D舰”
与该岛恰好在一条直线上，并测得“红方C舰”的俯角为300，测得“蓝方D舰”的俯角为80，请求出这时两舰之间的距离。
（参考数据：
）
4．如图所示，一勘测人员从B出发，沿坡度为150的坡面以5千米/时的速度行至D点，用了12分钟，然后沿坡度为200的坡面以3千米/时行至山顶A处，用了10分钟，求山高（即AC的长度）及A、B两点的水平距离。（即BC的长度）（精确到0.01千米）
(sin150=0.2588
, cos150=0.9659 , sin200=0.3420 , cos200=0.9397)
5．在生活中需要测量一些球（如足球、篮球……）的直径，某校研究学习小组，通过实验发现下面的测量方法：如图所示，将球放在水平的桌面上，在阳光的斜射下，得到球的影子AB，设光线DA、CB分别与球相切于点E、F，则EF即为球的直径，若测得AB的长为41.5cm，∠ABC=370，请你计算出球的直径（精确到1cm）。
 |
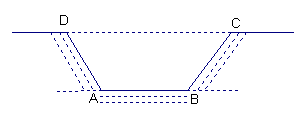6．某村计划开挖一条长1500米的水渠，渠道的断面为等腰梯形，渠道深0.8米，下底宽1.2米，坡角为450（如图所示）。实际开发渠道时，每天比原计划多挖20立方米，结果比原计划提前4天完成，求原计划每天挖土多少立方米。
7．在半径为27m的圆形广场中央点O上空安装了一个照明光源S，S射向地面的光束呈圆锥形，其轴截面SAB的顶角为1200（如图所示），求光源离地面的垂直高度SO（精确到0.1m）。（
，以上数据供参考）