初三上学期数学期中统一考试

（试卷满分：120分，考试时间：120分钟）

一、　　　  填空题：（满分32分，其中1—8题各3分、9—10题各4分）

1、方程x²=3x的解是　　　　　　　　　　　 ；

2、在函数y=中，自变量x的取值范围是　　　　　　  ；

3、如图1，在Rt△ABC中，∠C=90^o,

AB=3, AC= ，则tanA=　　　　　  ；

4、在实数范围内分解因式：x²+2x－1=　　　　　　　　  ；

5、若直线y=kx+b经过第一、二、三象限，则a·b　　 0（填上“>”或“<”或“=”）；

6、已知：－1是方程kx²+x－3=0的一个根，则方程的另一个根是　　　　　  ；

7、圆的一条弦长是12 cm，其弦心距为8cm，则圆的半径是　　 ；

8、如图2，B、C是河岸边的两点，

A是对岸边上的一点，测得∠ABC

=∠ACB=45^o, BC=60米，则点A

到对岸边BC的距离是　　　　  米。

9、如图3，已知AB是⊙O的直径，

BD=OB, ∠CAB=30^o, 请根据条件和

所给图形写出两个正确的结论（除AO=BO=BD外）：（1）　　　　　  、（2）　　　　　　  ；

10、在直径为10cm的圆中有两条长分别为6cm和8cm的平行弦，则这两条弦之间的距离为　　　　　　　　  。

二、　　　  选择题：（满分24分）

11、点P(-2，3)关于x轴对称的点的坐标（　  ）

（A）（-2，3） （B）（2，3） （C）（2，-3） （D）（-2，-3）

12、在△ABC中，∠C=90^o, ∠B=2∠A，则cosA等于（　　　）

　（A）　　 （B）　　 （C）　　  （D）

13、方程x²－x＋2=0根的情况是（　　　　  ）

（A）只有一个实数根　　　　 （B）有两个相等的实数根

（C）有两个不相等的实数根　 （D）没有实数根

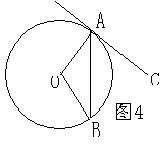14、如图4，CA是⊙O的切线，切点

为A点，点B在⊙O上，若∠BAC=55^o，

则∠AOB等于（　　）

（A）55^o　　　　　 （B）90^o　　

（C）110^o　　　　  （D）120^o

15、以和为两根的一元二次方程是（　　　 ）

（A）x²＋2x－1=0　　　　 （B）x²＋2x＋1=0

（C）x²－2x＋1=0　　　　 （D）x²－2x－1=0

16、如图5，PA切⊙O于点A，PO交⊙O于

点B，若PA=6, PB=4，则⊙O的半径为（　　　）

（A）1.25　　（B）2.5　 （C）2　　（D）5

17、小明同学骑自行车上学，开始以正常速度匀速行驶，后因途中自行车出故障，为能按时到校上课，故修好车后加快了骑车速度继续匀速行使。下面是行使路线S（米）与所用时间t（分钟）的函数图像，那么符合该同学行驶情况的图像大致是（　　　 ）

18、若圆的一条弦把圆分成1：3两条弧，则劣弧所对的圆周角的度数是（　　　 ）

　（A）45^o　　（B）90^o　　（C）135^o　　 （D）45^o或135^o

三、解答题：（满分共64分）

19、（6分）计算：

(2cos45^o－sin90^o)＋(tan60^o－)⁰＋(cot30^o－1)^－1＋tan44^otan46^o

20、（6分）已知直线y=kx＋b经过点（2，3）、（－1，－3）

（1）求k、b的值；（2）当x取何值时，y<0？

21、（7分）用换元法解方程：

22、（7分）已知：方程x²－x－1=0的两根为x₁、x₂，试求下列代数式的值。（1）（x₁＋1）（x₂＋1）　　　　 （2）x₁²＋x₂²

23、（7分）如图6，在Rt△ABC中，∠C=90^o, AC=3cm, BC=4cm, 以C为圆心，CA为半径的圆分别交AB、BC于D、E。求AB、AD的长。

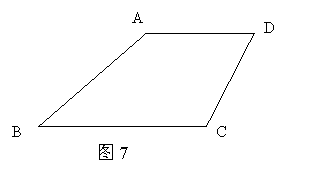24、（7分）如图7，已知：在梯形ABCD中，AD∥BC, ∠B=45^o,

∠C=120^o, AB=6cm。求CD的长。

25、（8分）某同学在测量体温时意识到体温计的读书与水银柱的长度之间可能存在着某种函数关系，就此他与同学们选择了一种类型的体温计，经历了收集数据、分析数据，得出结论的探索过程。他们收据到的数据如下：

体温计的读数t(oC)	35	36	37	38	39	40	41	42
水银柱的长度h(mm)	56.5	62.5	68.5	74.5	80.5	86.5	92.5	98.5

请你根据上述数据分析判断：水银柱的长度h(mm)与体温计的读数t（^oC）（35^o≤t≤42^o）之间存在什么样的函数关系？并根据你所学的知识求出函数解析式，画出函数图像。

26、（8分）如图8，在长300米、宽200米的长方形场地上修了三条不同形状的小路，剩余部分作为绿化区种植花草。已知三条小路的宽a、b、c都相等，且各条小路的两边分别平行。（1）请你通过观察和分析、判断1号路与2号路的面积有否相等？并简要说明理由； （2）若使绿化面积为53200米²，试求路的宽度。

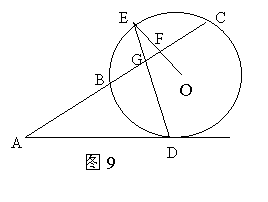
27、如图9，割线ABC与⊙O相交于B、C两点，D为⊙O

上一点，E为弧BC的中点，OE交BC于F点，DE交AC

于G点，∠ADG=∠AGD。（1）求证：AD是⊙O的切线；

（2）若AB=2, AD=4, EG=2, 求⊙O的半径。