初三数学总复习教案（五）
函数及其图象相关定理
1. 一一对应：
① 数轴上的点与实数一一对应。
② 坐标平面上的与有序实数对一一对应。
2．特殊位置的点的坐标特征：
① 横坐标上的点
纵坐标为零。
② 纵坐标上的点横坐标为零。
③ 平行于x轴的直线上的点纵坐标相等。
④ 平行于y轴的直线上的点横坐标相等。
⑤ 第一、三象限角平分线上的点横、纵坐标相等[设A点的坐标为（x,y）有x=y].
⑥ 第二、四象限角平分线上的点横、纵坐标互为相反数[设A点的坐标为（x,y）有x= - y].
2. 每一象限内点的坐标特征：设A（x,y）有
① 第一象限内的点x＞0,y＞0.
② 第二象限内的点x＜0,y＞0.
③ 第三象限内的点x＜0, y＜0.
④ 第四象限内的点x＞0, y＜0.
3. 设平面上点A（x
,y）,点B（x
,y）：
① AB在x轴上或平行于x轴AB=｜x- x｜。
② AB在y轴上或平行于y轴AB=｜y- y｜。
③ 点A到原点的距离OA=
。
④ 平面上任意两点AB的距离AB=
。
4. 对称的点的坐标特征：
① 点P（a,b）关于x轴的对称点的坐标P
（a,-b）。即：点P、P关于x轴对称横坐标相同、纵坐标互为相反数。
② 点P（a,b）关于y轴的对称点的坐标P
（-a,b）。即：点P、P关于x轴对称纵坐标相同、横坐标互为相反数。
③ 点P（a,b）关于原点对称的点的坐标P
（-a,-b）。即：点P、P
关于原点对称横、纵坐标均互为相反数。
5. 函数：设在一个变化过程中有两个变量x、y，对于x 的每一个值，y都有唯一的值与它相对应，则y叫做x的函数。其中x是自变量。
6. 函数的表示方法：解析法、图像法、列表法。
7. 一次函数一条直线y=kx+b(k,b是常数，k≠0)。
8. 正比例函数直线过原点y=kx(k是常数，k≠0)。
9. 反比例函数双曲线y=
(k是常数，k≠0) y=kx
(k是常数，k≠0) xy=k(k是常数，k≠0)
10. 二次函数抛物线y=ax
+bx+c(a、b、c是常数，且a≠0)。
11. 一次函数y=kx+b(k,b是常数，k≠0)的性质：
① 一次函数与y轴的交点为（0，b）,与x轴的交点为（-
,0）。
② k＞0时y随x的增大而增大，减小而减小。从左到右在上坡。
③ k＜0时y随x的增大而减小，减小而增大。从左到右在下坡。
④ b＞0时直线与y轴的交点在原点的上方。
⑤ b＜0时直线与y轴的交点在原点的下方。
⑥ b=0时直线经过原点。
⑦ 直线m∥nk
=k
⑧ 直线m、n交于x轴上同一点（
,0）
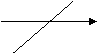
12. 一次函数y=kx+b(k,b是常数，k≠0)的图像：
① y ② y
 | |||
 | |||
x x
k＞0, b＞0图像过一、二、三象限。 k＞0, b=0图像过一、三象限。
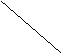
③ y ④ y
x
x
k＞0, b＜0图像过一、三、四象限。
k＜0, b＞0图像过一、二、四象限。
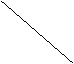⑤ y
⑥ y
x x
k＜0, b=0图像过二、四象限。
k＜0, b＜0图像过二、三、四象限。
13. 自变量的取值范围：
① 自变量所在的式子为整式时，自变量取全体实数。
② 自变量所在的式子含有分式时，则要求分母不为零。
③ 自变量所在的式子含有二根式（偶次方根）时，则要求二次根式（偶次方根）的被开方数为非负数。
④ 自变量所在的式子含有奇次方根时，则奇次方根的被开方数自变量取全体实数。
14. 反比例函数的性质：
① k＞0图象在第一、三象限内，在每一个象限内，y随x的增大而减小。
② k＜0图象在第二、四象限内，在每一个象限内，y随x的增大而增大。
③ 反比例函数图像的两个分支关于原点成中心对称。
15. 二次函数y=ax+bx+c(a、b、c是常数，且a≠0)的性质，设抛物线与x轴的交点为A（x,0）、B（x,0）;与y轴的交点C（0,c）有：
① a＞0抛物线的开口方向向上。
② a＜0抛物线的开口方向向下。
③ ｜a｜越大抛物线的开口越小; ｜a｜越小抛物线的开口越大。
④ c＞0抛物线与y轴的交点在原点的上方。
⑤ c＜0抛物线与y轴的交点在原点的下方。
⑥ c=0抛物线过原点。
⑦ a、b共同确定对称轴的位置的情况：（1）a、b同号，对称轴在y轴的左边；（2）a、b异号，对称轴在y轴的右边。简记：同号左，异号右。
⑧ △＞0抛物线与x轴有两个交点。
⑨ △=0抛物线与x轴有一个交点。
⑩ △＜0抛物线与x轴没有交点。
⑪ 二次函数y=ax+bx+c=a（x+
+
的顶点坐标为（
,）,对称轴为x=。
⑫ a＞0有：x＞y随x的增大而增大; x＜y随x的增大而减小。y≥有最小值。
⑬ a＜0有：x＞y随x的增大而减小; x＜y随x的增大而增大。Y≤有最大值。
⑭ AB=｜x－x｜=
。
⑮ 对称轴过最低点或最高点的直线过顶点的直线（平行于y轴）。
⑯ 顶点横坐标对称轴所在的直线最值顶点纵坐标。
16. 二次函数的三种表示方法：
① y=ax+bx+c(a、b、c是常数，且a≠0)。
② y=a(x－h)+k(a、h、k是常数，且a≠0)。
③ y=a(x — x)(x －x)(a是常数，且a≠0)。
17. 二次函数y=ax+bx+c(a、b、c是常数，且a≠0)的图象,设抛物线与x轴的交点为A（x,0）、B（x,0）,并设x＜x有：
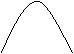
① y ② y ③ y
A B x
A(B) x x
④ y ⑤ ⑥ y
y A(B)
A B x x x
①△＞0,a＞0,b＜0,c＜0。y=ax+bx+c＞0x＜x或x＞x; y=ax+bx+c＜0 x＜x＜x.
④△＞0,a＜0,b＞0,c＞0。y=ax+bx+c＞0x＜x＜x; y=ax+bx+c＜0 x＜x或x＞x.
②△=0, a＞0,b＜0,c＞0。y=ax+bx+c＞0x≠的实数;y=ax+bx+c＜0无实数解。
⑤△=0, a＜0,b＞0,c＜0。y=ax+bx+c＞0无实数解;y=ax+bx+c＜0x≠的实数。
③△＜0，a＞0,b＜0,c＞0。y=ax+bx+c＞0全体实数; y=ax+bx+c＜0无实数解。
⑥△＜0，a＜0,b＞0,c＜0。y=ax+bx+c＞0无实数解;y=ax+bx+c＜0全体实数。
18. 设f（x）= ax+bx+c,一元二次方程ax+bx+c=0.的根的分布（a＞0）：
① 一根为零过原点c=0。
② 有一个正根和一个负根f（0）＜0。
③ 有一根大于a,一根小于af（a）＜0。
④ 有两个正根△≥0，＞0, f（0）＞0。
⑤ 有两个负根△≥0，＜0, f（0）＞0。
⑥ 有一个正根和一个负根,并且正根的绝对值大于负根的绝对值△≥0，＞0, f（0）＜0。
⑦ 有一个正根和一个负根,并且正根的绝对值小于负根的绝对值△≥0，＜0, f（0）＜0。
⑧ 两根都大于ｍ△≥0，＞m, f（ｍ）＞0。
⑨ 两根都小于ｍ△≥0，＜m, f（ｍ）＞0。
⑩ 一根在a、b之间，另一根在c、d之间（a<b<c<d）f (a) ＞0,f (b) ＜0,f (c) ＜0,f (d) ＞0.
⑪ 两根互为相反数对称轴为x=0b=0。
19. 绝对值不等式的解法：
①｜x｜＞a（a>0）x<－a或x > a，若a<0则x取全体实数。
②｜x｜< a（a>0）－a<x<a,若a<0则x无解。
20.练习：
① 抛物线通过（1,1）,（－1,3）,（2,
）三点，求解析式。
② 抛物线的顶点是（1,3）,且抛物线通过点（2,1）,求解析式。
③ 抛物线通过（－2,0）与（3,0）两点，并且与y轴的交点的纵坐标为－2，求解析式。
④ 一个一次函数的图象与一个反比例函数的图象相交于点A（1,2）,此一次函数的图象还经过点B（3,2）。求这两个函数的解析式。
⑤ 已知ｙ＋5与ｘ＋3成正比例，且当ｘ＝1时，y=3。（1）求ｙ与ｘ的函数关系式；（2）作出此函数的图象。
⑥ 已知抛物线y=ax+bx+c与ｙ轴交于点C，与ｘ轴交于点A（x，0）,B（x,0）（x＜x,顶点M的纵坐标为－4，若x，x是方程x－2（m－1）x+m－7的两根，且x+x=10. （1）求A、B两点的坐标; （2）求抛物线的解析式及点C的坐标;（3）在抛物线上是否存在点P，使三角形PAB的面积等于四边形ACMB的面积的2倍？若存在，求出符合条件的点的坐标若不存在，说明理由。
⑦ 已知抛物线y=－x+2x+3与x轴的交点为A,B,与y轴的交点为C，顶点为P。
（1） 求经过P，C的直线与x轴交点Q的坐标；
（2） 求tan∠PQB的值。
⑧ 已知抛物线y= x+5x+k与x轴两个交点间的距离等于3，与y轴交点为点C。直线y=kx+10与抛物线交A,B两点。求三角形ABC的面积。
⑨ 已知二次函数y=（m+2）x－（2m－1）x+m－3.
（1） 求证：无论m取任何实数，此二次函数的图象与x轴都有两个交点。
（2） 当m取何值时，二次函数的图象与x轴两个交点之间的距离等于2。
（3） 当m取何值时，二次函数的图象与x轴两个交点分布在y轴两侧。
⑩ 已知抛物线y= x－（m+8）x+2 m+12,
（1） 这个抛物线与x轴有几个交点？如果没有交点，请说明理由；如果有交点，能否判断交点的位置。
（2） 由（1）中若能得出抛物线与x轴有两个交点A,B且与y轴交于点C,如果△ABC的面积=80，能否求出m的值？
（3） 抛物线顶点为点P，是否存在实数m使△APB为等腰直角三角形？如果不存在，请说明理由。如果存在，请求出。