2004年上海市中等学校高中阶段招生文化考试

数学试卷

(满分120分，考试时间120分钟)

一、　　　　　 填空题：（本大题共14题，每题2分，共28分）

1．计算：．

2．不等式组的整数解是______________．

3．函数的定义域是__________________．

4．方程的根是________________．

5．用换元法解，可设，则原方程可化为关于的方程是______________．

6．一个射箭运动员连续射靶5次，所得的环数分别是8，6，10，7，9，则这个运动员所得环数的标准差为__________．

7．已知，则点A在第________象限．

8．正六边形是轴对称图形，它有_______条对称轴．

9．在△ABC中，点D、E分别在边AB、AC上，DE∥BC，AD=1，BD＝2，则=__________．

10．在△ABC中，∠A＝90°，设∠B＝，AC＝，则AB＝________(用和的三角比表示)．

11．某山路坡面坡度,沿此山路向上前进200米,升高了__________米．

12．在△ABC中，点G是重心，若BC边上的高为6，则点G到BC的距离为______________．

13．直角三角形的两条边长分别为6和8，那么这个三角形的外接圆的半径等于_______________．

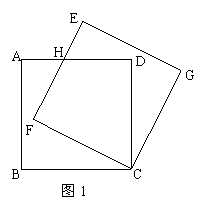
14．如图1，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到的正方形EFCG，EF交AD与点H，那么DH的长为___________．

二、　　　　　 多项选择题：(本大题共4题，每题3分，共12分)

【每题列出的四个答案中，至少有一个是正确的，把所有正确答案的代号填入括号内，错选或不选得0分，否则每漏选一个扣一分，直至扣完为止】

15．下列运算，计算结果正确的是……………………………………………（　　　　）

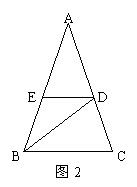（A） ；　（B） ；　（C） ；　（D） ．

16．如图2，在△ABC中，AB=AC，∠A＝36°，BD平分∠ABC，DE∥BC，

那么在下列三角形中，与相似的三角形是……………………（　　　　　  ）

（A） △DBE；　（B） △ADE；　（C） △ABD；　（D） △BDC．

17．下列命题中，正确的是…………………………（　　　　　  ）

（A）一个点到圆心的距离大于这个圆的半径，这个点在圆外；

（B）一条直线垂直于圆的半径，这条直线一定是圆的切线；

（C）两个圆的圆心距等于它们的半径之和，这两个圆有三条公切线；

（D）圆心到一条直线的距离小于这个圆的半径，这条直线与圆有两个交点．

18．在函数的图像上有三点、、，已知，则下列各式中，正确的是…………………………（　　　　 ）

（A） ；　　　　　　　　　　  （B） ；

（C） ；　　　　　　　　　　 （D） ．

三、（本大题共4题，每题7分，共28分）

19．化简：．

20．关于的一元二次方程，其根的判别式的值为1，求的值及该方程的根．

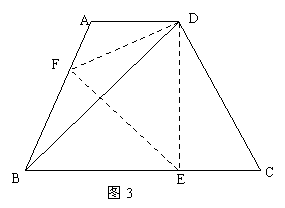
21．如图3，等腰梯形ABCD中，AD∥BC，∠DBC＝45°，翻折梯形ABCD，使点B重合于点D，折痕分别交AB、BC于点F、E．若AD=2，BC＝8，

求：（1）BE的长；　（2）∠CDE的正切值．

22．某区从参加数学质量检测的8000名学生中，随机抽取了部分学生的成绩作为样本，为了节省时间，先将样本分成甲、乙两组，分别进行分析，得表一；随后汇总成样本数据，得到部分结果，如表二．

　　　　表一　　　　　　　　　　　　　　　　　　 表二　　　　　　　　　　　　　　 

	甲 组	乙 组		分数段
				频数	3	6	36		50	13
人数（人）	100	80		频率			20％	40％
平均分（分）	94	90		等第	C		B		A

请根据表一、表二所示的信息回答下列问题：

（1）样本中，学生的数学成绩的平均分数约为_________分（结果精确到0.1分）；

（2）样本中,数学成绩在分数段的频数________，等第为A的人数占抽样学生总数的百分比为_________，中位数所在的分数段为______________；

（3）估计这8000名学生成绩的平均分数约为__________分（结果精确到0.1分）．

四、（本大题共4题，每题10分，共40分）

23．在平面直角坐标系中，点O是坐标原点，二次函数的图像交轴于A、B，且．

（1）求二次函数的解析式；

（2）将上述二次函数的图像沿轴向右平移2个单位，设平移后的图像与轴的交点为C，顶点为P，求△POC的面积．

24．如图４，在△ABC中，∠BAC＝90°，延长BA到点D，使AD＝AB，点E、F分别为边BC、AC的中点．

（1）求证：DF=BE；

（2）过点A作AG∥BC，交DF于点G，求证：AG=DG．

25．为加强防汛工作，市工程队准备对苏州河一段长为2240米的河堤进行加固．由于采用新的加固模式，现在计划每天加固的长度比原计划增加了20米，因而完成此段加固工程所需天数将比原计划缩短2天．为进一步缩短该段加固工程的时间，如果要求每天加固224米，那么在现在计划的基础上，每天加固的长度还要再增加多少米？

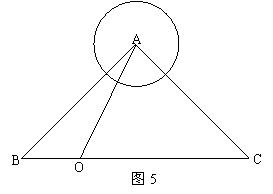
26．在△ABC中，∠BAC＝90°，AB=AC=，⊙A的半径为1，如图5所示．若点O在BC上运动（与点B、C不重合），设BO＝，△AOC的面积为

（1）求关于的函数解析式，并写出函数的定义域；

（2）以点O为圆心，BO长为半径作⊙O，求当⊙O与⊙A相切时，△AOC的面积．

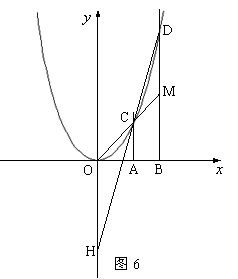
五、（本大题只有1题，满分12分，（1）小题满分6分，（2）（3）小题满分均为3分）27．数学课上，老师出示图6和下面框中的条件．

同学发现两个结论：①　　②数值相等关系：

（1）请你验证结论①和结论②成立；

（2）请你研究：如果上述框中的条件“A的坐标(1，0)”改为“A的坐标(t，0) (t>0)”，其他条件不变，结论①是否仍成立？（请说明理由）

（3）进一步研究：如果上述框中的条件“A的坐标(1，0)”改为“A的坐标(t，0) (t>0)”，又将条件“”改为“”， 其他条件不变，那么、与有怎样的数值关系？写出结果并说明由）[1]

---