二00二年福州市初中毕业会考、高级中等学校招生考试
![]() 数 学 试 卷 座位号
数 学 试 卷 座位号
(满分:150分:考试时间:120分钟)
| 题 号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总 分 |
| 得 分 |
|
| 评 卷 人 | |||
 1.-5的相反数是 .
1.-5的相反数是 .
2.分解因式:a3-ab2= .
3.在函数y =![]() 中,自变量x的取值范围是
.
中,自变量x的取值范围是
.
4.计算:![]() =
.
=
.
5.六边形的内角和等于 度.
6.如图:某地的等高线示意图,图中a、b、c为等高线,海拔
最低的一条为60米,等高距为10米,结合地理知识写出
等高线a为 米,b为 米,c为 米.
7.已知:线段a=4cm,b=9cm,则线段a、b的比例中项c为________cm.
8.用换元法解分式方程:x![]() + x +
+ x +![]() =3, 设y =x
=3, 设y =x![]() +x,那么原方程化
+x,那么原方程化
为y的一元二次方程的一般形式为____________________________.
9.如图:在⊙O中,直径AB=4cm,弦CD⊥AB于E,OE=![]() ,则弦CD的长为 cm.
,则弦CD的长为 cm.
10.若圆锥的底面直径为6cm,母线长为5cm,则它的侧面积为 cm2(结果保留π).
 11. 已知:x
11. 已知:x![]() - x-1=0,则-
- x-1=0,则- ![]() x
x![]() +2 x2+2002的值为
。
+2 x2+2002的值为
。
12.如图:四边形ABCD是正方形,曲线DA1B1C1D1…叫做“正方形的
渐开线” ,其中![]() DA1、A1B1、B1C1、C1D1、…的圆心依次按A、
DA1、A1B1、B1C1、C1D1、…的圆心依次按A、
B、C、D 循环,它们依次连接,取AB=1,则曲线DA1B1…C2D2
的长是 (结果保留π)。
| 得 分 |
| |||
13.下列运算不正确的是 ( )
(A)(a5)2 = a10 (B)2a2·(-3a3)=-6a5 (C)b·b3=b4 (D)b5·b5=b25
14. 如果反比例函数y=![]() 的图象经过点(-2,-1),那么k的值为
( )
的图象经过点(-2,-1),那么k的值为
( )
(A)![]() (B)-
(B)-![]() (C)2 (D)-2
(C)2 (D)-2
15.下列二次根式中,属于最简二次根式的是 ( )
A、![]() B、
B、![]() C、
C、 ![]() D、
D、 ![]()
16.等腰三角形的两边长分别为2和7,则它的周长是 ( )
 A、9 B、11
C、16 D、11或16
A、9 B、11
C、16 D、11或16
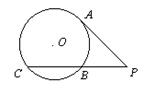
17.如图:PA切⊙O于点A,PBC是⊙O的一条割线,
且PA=3![]() ,PB=BC,那么BC的长是
( )
,PB=BC,那么BC的长是
( )
A、3 B、3![]() C、
C、![]() D、2
D、2![]()
18.下列四个命题中错误的是 ( )
A、两条对角线互相平分的四边形是平行四边形
B、两条对角线相等的四边形是矩形
C、两条对角线互相垂直的矩形是正方形
D、两条对角线相等的菱形是正方形
19.某市在“旧城改造”中计划在市内一块如图所示的三角形空地上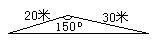 种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要
( )
种植某种草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要
( )
A、450a元 B、225a元 C、 150a元 D、 300a元
20.已知:二次函数y=x2+bx+c与x轴相交于A(x1,0)、B(x2,0)两点, 其顶点坐标为
P(-![]() ,
,![]() ), AB=
), AB=![]() ,若S△APB=1,则b与c的关系式是
( )
,若S△APB=1,则b与c的关系式是
( )
A、b2-4c+1=0 B、b2-4c-1=0 C、b2-4c+4=0 D、b2-4c-4=0
|
| 评 卷 人 | |||
21、解不等式组:![]()
![]() 并把它的解集在数轴上表示出来;
并把它的解集在数轴上表示出来;
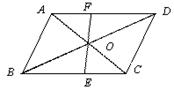
22.如图:已知,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O,且与BC、AD分别相交于点E、F.
求证:OE=OF;
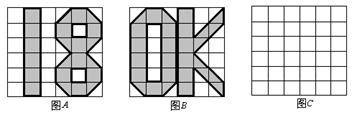
23.已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为SA、SB(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题.
1). 填空:SA:SB的值是 .
2). 请在图C的网格上画出一个面积为8个平方单位的中心对称图形;
24.随机抽取某城市一年(365天)中的30天的日平均气温状况统计如下:
| 温度(x0C) | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
| 天数t | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
请根据上述数据填空:
1)该组数据的中位数是 0C;
2)该城市一年中日平均气温为260C的约有 天;
3)若日平均气温在170C-230C为市民“满意温度”,则该城市一年中达到市民“满意温度”的约有 天.
| 得 分 |
| |||
25. 为落实“珍惜和合理利用每一寸土地”的基本国策。某地区计划经过若干年开发“改造后可利用土地”360平方千米,实际施工中,每年比原计划多开发2平方千米,按此进度预计可提前6年完成开发任务,问实际每年可开发多少平方千米?
|
| 得 分 | 评 卷 人 | |
26.已知:二次函数y=x2+bx+c(b、c为常数).
(1)若二次函数的图象经过A(-2,-3)和B(2,5)两点,求此二次函数的解析式;
(2)若(1)中的二次函数的图象过点P(m+1,n2+4n),且m≠n,求m+n的值.
|
| 评 卷 人 | |||
27.已知:半径不等的⊙O1与⊙O2相切于点P,直线AB、CD都经过切点P,并且AB分别交⊙O1、⊙O2于A、B两点,CD分别交⊙O1、⊙O2于C、D两点(点A、B、C、D、P互不重合),连结AC和BD.
1) 请根据题意画出图形;
2) 根据你所画的图形,写出一个与题设有关的正确结论,并证明这个结论(结论中不能出现题设以外的其他字母).
|
| 评 卷 人 | |||
D在AB边上移动(不与A、B重合),DE‖BC,交AC于E,连结CD,设S△ABC=S,S△DEC=S1 。
(1) 当D为AB中点时,求S1:S的值。
(2) 若AD=![]() ,
, ![]() =
=![]() ,求
,求![]() 关于
关于![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围。
的取值范围。
(3) 是否存在点D,使得S1>![]() S成立?
S成立?
若存在,求出D点位置;若不存在在,请
说明理由。
|
| 评 卷 人 | |||
29. 已知:矩形ABCD在平面直角坐标系中,顶点A、B、D的坐标分别为A(0,0),
B(m,0),D(0,4),其中m≠0。
(1) 写出顶点C的坐标和矩形ABCD的中心P点的坐标。(用含m的代数式表示);
(2) 若一次函数y=kx -1的图象l把矩形ABCD分成面积相等的两部分,求此一次函数的解析式(用含m的代数式表示);
(3) 在(2)的前提下,l又与半径为1的⊙M相切,且点M(0,1),求此时矩形ABCD的中心P点的坐标。
二00二年福州市初中毕业会考、高级中等学校招生考试
数学试卷评分标准及参考答案
说明:1.考生的解法与“参考答案”不同时,可参照“答案”的评分标准进行评分。
2.以下解答各行右端所注分数表示正确做完该步应得的分数。
3.评分最小单位是1分,得分或扣分都不出现小数。
一、(每小题3分,共36分)
(1)5 (2)a (a+b) (a-b) (3)![]() (4)
(4)![]() (5)720 (6)60,70,80 (7)6
(5)720 (6)60,70,80 (7)6
(8)![]() y2-3y+1=0
(9)2 (10)15
y2-3y+1=0
(9)2 (10)15![]() (11)2003 (12)18
(11)2003 (12)18![]()
二、(每小题4分,共28分)
(13)D (14)C (15)D (16)C (17)A (18)B (19)C (20)D
三、(每小题7分,共28分)
21.解不等式(1)得:![]() (3分)
(3分)
解不等式(2)得:![]() (5分)
(5分)
![]() 原不等式组的解集是:-2
原不等式组的解集是:-2![]() (6分)
(6分)
原不等式组解集在数轴上表示如下:
![]()
22.证法一:![]() 平行四边形
平行四边形![]() ABCD
(7分)
ABCD
(7分)
![]() ∴AD∥BC OA=OC
(2分)
∴AD∥BC OA=OC
(2分)
且∠CAD=∠ACB(或∠AFO=∠CEO)
又∵∠AOF=∠COE (写出满足全等的条件得4分)
∴△AOF≌△COE (6分)
∴OE=OF (7分)
证法二:∵ 平行四边形 ABCD
∴AD∥BC OA=OC (2分)
∴![]()
![]() (6分)
(6分)
∴OE=OF (7分)
23.①SA:SB=![]() (3分)
(3分)
②画出图形具有中心对称得2分,面积为8个平方单位得2分(参考答案见第4页)
24.(1)22 (3分)
(2)73 (2分)
(3)146 (2分)
四、(本题10分)
25.解:设实际每年可开发![]() 平方千米
(1分)
平方千米
(1分)
则依题意得:
![]() (6分)
(6分)
整理得![]() (7分)
(7分)
解得:∴ ![]()
![]() (9分)
(9分)
经检验: ![]()
![]() 都是原方程的解, 但
都是原方程的解, 但![]() 不合题意舍去,
不合题意舍去,
所以只取![]()
答:实际每年可开发12平方千米。 (10分)
注:检验与答案缺一个或二个都只扣1分。
五、(本题第(1)小题6分,第(2)小题4分,共10分)
26.解:①依题意得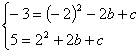 (2分)
(2分)
解得:![]()
![]() (5分)
(5分)
∴所求二次函数的解析式是:![]() (6分)
(6分)
解:②∵二次函数图象过点![]()
![]()
∴![]() (7分)
(7分)
![]() (8分)
(8分)
![]() (9分)
(9分)
∵![]() ∴
∴![]()
即![]() (10分)
(10分)
六、(本题第(1)小题4分,第(2)小题6分,共10分)
27.(1)正确画出每个图形各得2分。
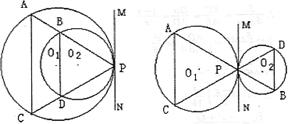
(2)解答:(以两圆外切为例,内切评分标准与外切对应得分)
第一种结论:AC∥BD (6分)
证明:过P作两圆的公切线MN (7分)
∴∠MPA=∠C ∠NPB=∠D (8分)
∵∠APM=∠NPB ∴∠C=∠D (9分)
∴AC∥BD (10分)
第二种结论:△APC∽△BPD (6分)
证明:过P作两圆公切线MN (7分)
∴∠MPA=∠C,∠NPB=∠D (8分)
∵∠APM=∠NPB ∴ ∠C=∠D (9分)
又∵∠APC=∠BPD
∴△APC∽△BPC (10分)
第三种结论:O1、P、O2三点共线(或连心线O1O2必过切点P), (6分)
证明:∵①圆是轴对称圆形
②相切的两圆也组成一个轴对称圆形
③连心线O1O2是两圆的对称轴
∴O1、P、O2三点共线(或连心线O1O2必过切点P) (10分)
注:(每写一点各得1分)
七、(本题第(1)小题3分,第(2)小题4分,第(3)小题5分,共12分)
28.解(1)∵DE∥BC,D为AB的中点
∴△ADE∽△ABC,![]() (1分)
(1分)
∴![]() (2分)
(2分)
∵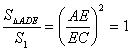
∴![]() (3分)
(3分)
解(2)∵![]()
∴![]() (4分)
(4分)
又∵![]()
∴![]()
∴![]() (5分)
(5分)
∴![]()
即![]() (6分)
(6分)
自变量![]() 的取值范围是:
的取值范围是:![]() (7分)
(7分)
解(3):不存在点D,使得![]() 成立
(8分)
成立
(8分)
理由:假设存在点D,使得![]() 成立
成立
那么![]() 即
即 ![]()
∴![]()
![]() (10分)
(10分)
∵![]()
∴![]() 不存在
不存在
即不存在点D,使得![]() 成立
(12分)
成立
(12分)
 29.(本题第(1)小题3分,第(2)小题4分,第(3)小题5分,共12分)
29.(本题第(1)小题3分,第(2)小题4分,第(3)小题5分,共12分)
(23题第(2)小题参考答案)
解:(1)C点坐标为(m,4) (1分)
P点坐标为![]() (3分)
(3分)
(2)∵直线![]() 把矩形ABCD分成面积相等两部分:
把矩形ABCD分成面积相等两部分:
∴![]() 必过中心点
必过中心点![]() (4分)
(4分)
∴![]() (5分)
(5分)
∵![]() , ∴
, ∴![]() (6分)
(6分)
∴![]() (7分)
(7分)
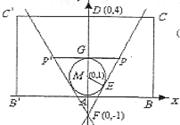
(3)设直线![]() 与
与![]() 轴相交于点F
轴相交于点F
∴F点坐标为(0,-1)
∵⊙M的半径为1,
∴![]()
∴![]() (8分)
(8分)
过P作PG⊥![]() 轴于G
轴于G
∴![]()
∴![]()
∴![]()
![]() (10分)
(10分)
∴P点坐标为![]()
或![]() (12分)
(12分)
![]()