北京市丰台区2005年初中毕业会考
第I卷 (选择题 共48分)
一. 选择题:每题均有四个选项,其中只有一个是符合题意的。(本题共48分,每小题3分)
1. 7的相反数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2. 4的平方根是
A. 8 B.
2 C.
![]() D.
D.
![]()
3. 用科学记数法表示0.0032为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
4. 如果两圆相交,那么两圆的公切线共有
A. 4条 B. 3条 C. 2条 D. 1条
5. 在函数![]() 中,自变量x的取值范围是
中,自变量x的取值范围是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6. 下列运算中,错误的是
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
7. 如图,A、B、C三点在⊙O上,且![]() ,则
,则![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()

8. 七边形的内角和是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
9. 下列各式中与![]() 是同类二次根式的是
是同类二次根式的是
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
10. 若反比例函数![]() 的图象经过点A(2,m),则m的值是
的图象经过点A(2,m),则m的值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
11. 计算![]() 的结果是
的结果是
A. ![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
12. 下列多边形中,既是轴对称图形又是中心对称图形的是
A. 平行四边形 B. 正方形 C. 等腰梯形 D. 等边三角形
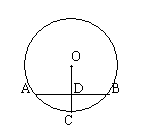
13. 如图,AB是⊙O的弦,半径![]() 于点D,且AB=8cm,
于点D,且AB=8cm,![]() ,则OD的长是
,则OD的长是
A. ![]() B.
B.
![]() C.
C. ![]() D.
1cm
D.
1cm
14. 圆柱的高为6cm,它的底面半径为4cm,则这个圆柱的侧面积是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
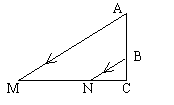
15. 如图是一束平行的光线从教室窗户射入教室的平面示意图,测得光线与地面所成的角![]() ,窗户的高在教室地面上的影长MN=
,窗户的高在教室地面上的影长MN=![]() 米,窗户的下檐到教室地面的距离BG=1米(点M、N、C在同一直线上),则窗户的高AB为
米,窗户的下檐到教室地面的距离BG=1米(点M、N、C在同一直线上),则窗户的高AB为
A. ![]() 米 B.
米 B. ![]() 米 C.
2米 D.
1.5米
米 C.
2米 D.
1.5米
16. 已知二次函数![]() 的图象如图所示,下列结论:
的图象如图所示,下列结论:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (4)
(4)![]() 。其中正确的结论有:
。其中正确的结论有:
A. 4个 B. 3个 C. 2个 D. 1个

第II卷 (非选择题 共52分)
二. 填空题:(本题共12分,每小题3分)
17. 等腰三角形的两边长分别为5cm和2cm,则它的周长是________cm。
18. 为了调查某一路口某时段的汽车流量,交警记录了一个星期同一时段通过该路口的汽车辆数,记录的情况如下表:
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 汽车辆数 | 100 | 98 | 90 | 82 | 100 | 80 | 80 |
那么这一个星期在该时段通过该路口的汽车平均每天为_______辆。
19. 若无理数a满足不等式![]() ,请写出两个符合条件的无理数_______、_______。
,请写出两个符合条件的无理数_______、_______。
20. 观察下列数表:
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
4 5 6 7 … 第四行
![]()
![]()
![]()
![]()
第 第 第 第
一 二 三 四
列 列 列 列
根据表中所反映的规律,猜想第6行与第6列的交叉点上的数应为______,第n行(n为正整数)与第n列的交叉点上的数应为_________。
三. (本题共10分,每小题5分)
21. 计算:![]()
解:
22. 分解因式:![]()
解:
四. (本题6分)
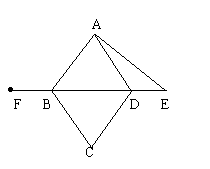
23. 已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF。请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)。
(1)连结____________;
(2)猜想:______=______;
(3)证明:
五. (本题共12分,每小题6分)
24. 用换元法解方程:![]()
解:
25. 列方程或方程组解应用题:
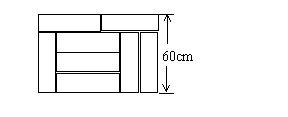
用8块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示,求每块地砖的长与宽。
解:
六. (本题6分)
26. 如图,已知平面直角坐标系中三点A(2,0),B(0,2),P(x,0)![]() ,连结BP,过P点作
,连结BP,过P点作![]() 交过点A的直线a于点C(2,y)
交过点A的直线a于点C(2,y)
(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标。
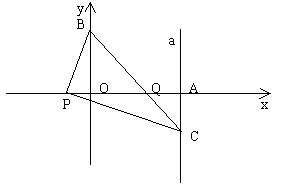
解:
七. (本题6分)
27. 在直角坐标系中,⊙![]() 经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
(1)如图,过点A作⊙![]() 的切线与y轴交于点C,点O到直线AB的距离为
的切线与y轴交于点C,点O到直线AB的距离为![]() ,求直线AC的解析式;
,求直线AC的解析式;
(2)若⊙![]() 经过点M(2,2),设
经过点M(2,2),设![]() 的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
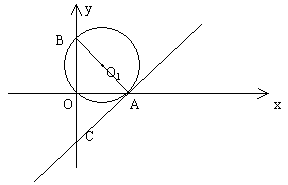
解:
试题参考答案及评分标准
第I卷(选择题 共48分)
一. 选择题:每题均有四个选项,其中只有一个是符合题意的。(本题共48分,每小题3分)
1. A 2. C 3. B 4. C 5. D 6. B 7. D 8. C
9. D 10. C 11. D 12. B 13. A 14. A 15. C 16. B
第II卷 (非选择题 共52分)
二. 填空题(本题共12分,每小题3分)
17. 12; 18.
90 19.
略 20.
11,![]()
说明:19小题只写出一个符合题意的无理数给1分;20小题第1个空1分,第2个空2分。
三. (本题共10分,每小题5分)
21. 计算:![]()
解:![]()
![]() 4分
4分
![]()
![]() 5分
5分
说明:其中![]() ,
,![]() 各给2分
各给2分
22. 分解因式:![]()
解:![]()
![]() 1分
1分
![]() 3分
3分
![]() 5分
5分
四. (本题6分)
23. 已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF。请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)。
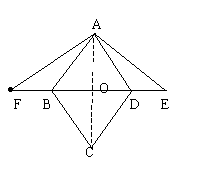
(1)连结____________;
(2)猜想:______=______;
(3)证明:
说明:(1)连结线段正确给1分(连结的线段画成虚线或实线均给分);(2)猜想正确给1分;(3)证明过程正确给4分。
(3)证法一:(连结AF,猜想AF=AE)
连结AC,交BD于O
![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() 于O,DO=BO 2分
于O,DO=BO 2分
![]() 3分
3分
![]() 垂直平分EF
垂直平分EF
![]() 4分
4分
说明:![]() 于O,DO=BO各给1分
于O,DO=BO各给1分
证法二:![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() , 1分
, 1分
![]() ,
,
![]() 2分
2分
在![]() 中
中
![]() 3分
3分
![]() 4分
4分
五. (本题共12分,每小题6分)
24. 用换元法解方程:![]()
解:设![]() , 1分
, 1分
那么![]() ,
,
于是原方程变形为 ![]() 2分
2分
方程的两边都乘以y,约去分母,并整理,得![]()
解这个方程,得![]() ,
,![]() 3分
3分
当![]() 时,
时,![]() ,即
,即![]()
解这个方程,得![]() 4分
4分
当![]() 时,
时,![]() ,即
,即![]()
因为![]() ,所以,这个方程没有实数根 5分
,所以,这个方程没有实数根 5分
经检验,![]() 都是原方程的根。 6分
都是原方程的根。 6分
![]() 原方程的根是
原方程的根是![]()
25. 列方程或方程组解应用题:
用8块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示,求每块地砖的长与宽。

解:设每块地砖的长为xcm,宽为ycm 1分
根据题意,得
![]() 3分
3分
解这个方程组,得 ![]() 5分
5分
答:每块地砖的长为45cm,宽为15cm 6分
六. (本题6分)
26. 如图,已知平面直角坐标系中三点A(2,0),B(0,2),P(x,0)![]() ,连结BP,过P点作
,连结BP,过P点作![]() 交过点A的直线a于点C(2,y)
交过点A的直线a于点C(2,y)
(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标。

解:(1)![]()
![]()
![]() A(2,0),C(2,y)在直线a上
A(2,0),C(2,y)在直线a上
![]()
![]() 2分
2分
![]() ,
,![]() ,
,
![]()
![]() 4分
4分
(2)![]() ,
,![]() 的最大整数值为
的最大整数值为![]()
当![]() 时,
时,![]() ,
,![]()
![]()
设Q点坐标为![]() ,则
,则![]()
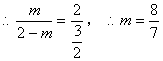
![]() 点坐标为
点坐标为![]() 6分
6分
七. (本题6分)
27. 在直角坐标系中,⊙![]() 经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B。
(1)如图,过点A作⊙![]() 的切线与y轴交于点C,点O到直线AB的距离为
的切线与y轴交于点C,点O到直线AB的距离为![]() ,求直线AC的解析式;
,求直线AC的解析式;
(2)若⊙![]() 经过点M(2,2),设
经过点M(2,2),设![]() 的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
的内切圆的直径为d,试判断d+AB的值是否会发生变化,如果不变,求出其值,如果变化,求其变化的范围。
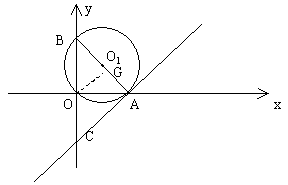
图1
解:(1)如图1,过O作![]() 于G,则
于G,则![]()
设![]()
![]()
![]()
![]()
![]()
![]() (3,0) 1分
(3,0) 1分
![]() AB是⊙
AB是⊙![]() 的直径
的直径
![]() 切⊙
切⊙![]() 于A,
于A,![]()
在![]() 中
中
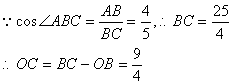
![]() 2分
2分
设直线AC的解析式为![]() ,则
,则
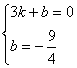
![]()
![]() 直线AC的解析式为
直线AC的解析式为![]() 4分
4分
(2)结论:![]() 的值不会发生变化 5分
的值不会发生变化 5分
设![]() 的内切圆分别切OA、OB、AB于点P、Q、T,如图2所示
的内切圆分别切OA、OB、AB于点P、Q、T,如图2所示
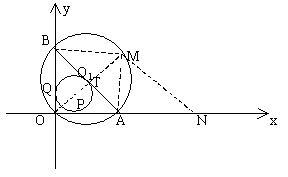
图2
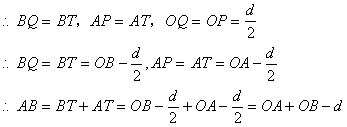
则![]()
在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN
![]() 平分
平分![]()
![]()
![]()
![]()
![]() 6分
6分
![]() 的值不会发生变化,其值为4。
的值不会发生变化,其值为4。