第一章 代数式初步知识
1. 代数式是用 (包括 )把 、 连接而成的式子.注意 ①单独的一个数或一个字母也是代数式;②在代数式中出现的乘号,通常 或 ,如将4×a通常写成 ( 应写在字母前),但 与 相乘一般仍用“×”;③在代数式中出现除法运算时,一般按照 的写法来写;④若代数式是多项式的形式且后面有单位,则代数式需加 .
2. 两个数相加,交换加数的位置, .用式子表示为 ,这是 律.
3. 三个数相加,先把 相加,或者先把 相加, 不变.用式子表示为 .这是加法 .
4. 两个数相乘, , .用式子表示为 ,这是 .
5. 三个数相乘,先把前两个数相乘,或者先把 , .用式子表示为 .这是 .
6. 一个数同两个数的和相乘,等于把这个数 ,再把 .用式子表示为 .
7. 平方和表示先 ,再 ;而和的平方表示先 ,再 .
8. 用 代替代数式里的字母,按照 , ,叫做代数式的值.
9. 叫做解方程.
10. 叫做方程.
11. 叫做方程的解.
12. 方程同解原理1指
.
13. 方程同解原理2指
.
第二章 有理数
1. ,叫做正数, 叫做负数,0 .
2. 统称整数, 统称分数.
3. 规定了 、 和 的直线叫做数轴。数轴上的点和 一一对应.
4. 在数轴上表示的两个数, 的数比 的数大.正数 ,负数 ;正数 一切负数.
5.
①只有
的两个数,其中一个是另一个的相反数.只有 的相反数是它本身。②a的相反数是 .③在数轴上的原点 ,离开原点的
的两个点所表示的两个数是互为相反数;④ (数学式子)![]() a、b互为相反数.
a、b互为相反数.
6.
①一个数a的绝对值就是数轴上表示数a的点
.数a的绝对值记作 .②一个正数的绝对值是 ;一个负数的绝对值是
;零的绝对值是 .用式子表示为: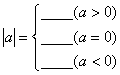 。
。
7. 两个负数,绝对值 .
8. 绝对值是它本身的数是 .
9. 有理数加法法则:①同号两数相加,取 的符号,并把 相加;②绝对值不相等的异号两数相加,取 的符号,并把 减去 .互为相反数的两个数相加得 ;③一个数同 相加,仍得这个数. 练习:用不等号填空.⑴如果a>0,b>0,那么a+b 0; ⑵如果a<0,b<0,那么a+b 0; ⑶如果a>0,b<0,a<b,那么a+b 0;⑷如果a<0,b>0,a>b,那么a+b 0.
10. 有理数减法法则:减去一个数,等于加上 . 练习:用不等号填空.⑴如果a>0,b<0,那么a-b 0; ⑵如果a<0,b>0,那么a-b 0; ⑶如果a<0,b<0,a<b,那么a-b 0;⑷如果a<0,b<0,那么a-(-b) 0.
11. 代数和是指 .
12. 有理数乘法法则:两数相乘, , ,并把 相乘;任何数同 相乘,都得0.
13. 几个 的数相乘,积的符号由 决定.当 时,积为负;当 时,积为正.几个数相乘,有一个因数为0,积就为 .
14. 有理数除法法则:除以一个数等于 .用式子表示为 a÷b= .注意 不能作除数.
15. 两数相除, , ,并把 相除;0除以 ,都得0.
16.
的运算,叫做乘方.乘方的结果叫做 .(读作 ).在a![]() 中,a叫做 ,n叫做 .a
中,a叫做 ,n叫做 .a![]() 读作 或
.
读作 或
.
17. 正数的 ;负数的 是负数,负数的 是正数.
18. 科学记数法是指任何数记成 的形式,其中用式子表示a的范围是 .练习:用科学记数法表示下列各数:①=
②-= ③0.009403=
④-0.= ⑤9= ⑥10000=
19. 有理数运算顺序:先算 ,再算 ,最后算 .如果有 ,就先算 .
20.
从
起,到
止, 的数字,都叫做这个数的有效数字.练习:用四舍五入法按要求取近似值:①0.85149(精确到千分位) ②547.5(精确到个位)
③1.59501(精确到0.01) ④604999(保留两个有效数字) ⑤3.04×10![]() (精确到千位)
(精确到千位)
填空:⑥由四舍五入得到的近似数3.010×10![]() 精确到 位,有 个有效数字.
精确到 位,有 个有效数字.
第三章 整式的加减
1. 的代数式叫做单项式.单项式中的 叫做这个单项式的系数.一个单项式中, 叫做这个单项式的次数.
2. 叫做多项式.在多项式中,每个 叫做多项式的项.其中, 的项叫做常数项.多项式里, ,就是这个多项式的次数.
3. 把一个多项式按 的顺序排列起来,叫做把多项式按这个字母降幂排列.把一个多项式按 的顺序排列起来,叫做把多项式按这个字母升幂排列.
4. 和 统称整式.
5. 相同, 也相同的项叫做同类项.几个常数项 同类项.
6. 合并同类项的法则:同类项的 相加,所得的结果作为 , 不变.
7. 去括号法则:括号前面是“+”号,把括号和 去掉,括号里 ;括号前面是“—”号,把括号和 去掉,括号里 .
8. 添括号法则:添括号后,括号前面是“+”号,括到括号里的 .添括号后,括号前面是“—”号,括到括号里的 .
第四章 一元一次方程
1. 等式性质1:
.
2. 等式性质2:
.
3. 叫做方程的根.
4. 移项要 .
5. 只含有 ,并且 ,系数 的方程叫做一元一次方程.它的最简形式为 .一元一次方程的标准形式为 .
6. 解一元一次方程的一般步骤是:
①
②
③
④
⑤
7. 原方程的小数化为整数,是根据 . 而去分母是根据 .
8. 列出一元一次方程解应用题的方法:
① 审:
② 找:
③ 列:
④ 解:
⑤ 写:
第五章 二元一次方程
1. 含有 未知数,并且 的方程叫做二元一次方程.
2. 由几个(一般是两个) 组成并含有 相同未知数的方程组是二元一次方程组.
3. 一般地,使二元一次方程组的每个方程
叫做二元一次方程组的解.
4. 解方程组的基本思想是: ;基本方法是: 和 .
第六章 一元一次不等式和 一元一次不等式组
1. ,叫做不等式.
2. 不等式基本性质1:
.
3. 不等式基本性质2:
.
4. 不等式基本性质3:
.
5. 一个 组成这个不等式的解集合,简称这个不等式的解集.
6. ,叫做解不等式.
7. 一元一次不等式是指: ,它的标准形式是 或 .
8. 不等式同解原理1:
.
9. 不等式同解原理2:
.
10. 不等式同解原理3:
.
11. 几个一元一次不等式的 ,叫做由它们所组成的一元一次不等式组的解集.
12. ,叫做解不等式组.
13. 解一元一次不等式组可以分为以下两个步骤:
⑴
⑵
14. 等式与不等式的性质和解法比较此处略,详见《代数》第一册下P76-P77.
第七章 整式的乘除
1. 同底数幂相乘, , .用式子表示为 .
2. 幂的乘方, , .用式子表示为 .
3. 积的乘方, ,再把 .用式子表示为 .
4. 单项式相乘,把它们的 、 分别相乘,对于 ,则连同 作为积的一个因式.
5. 单项式和多项式相乘,就是用 去乘 ,再把 .
6. 多项式与多项式相乘,先用 乘以 ,再把 .
7. 平方差公式:
.用式子表示为 .
8. 完全平方公式:
.用式子表示为 .
9. 立方和与立方差公式:
.用式子表示为 .
10.
(a+b+c)![]() = .
= .
11.
(a±b)![]() =
.
=
.
12. 同底数幂相除, , .用式子表示为 .
13. 任何 的数0次幂都等于 .用式子表示为 .
14. 任何 的数的 – P次幂( ),等于这个数的 .用式子表示为 .
15. 单项式相除,把 、 分别相除,作为 ,对于只在 ,则连同 作为 .
16. 多项式除以单项式,先把 除以 ,再把 .
第八章 因式分解
1. 叫做把这个多项式因式分解.常用的方法有: 、
、 、 和 .
2. 如果多项式的 有公因式,可以把 提到括号外面,将公因式写成 的形式,这种分解因式的方法叫做提公因式法.
3.
![]() .
.
4.
把![]() 分解因式时:
分解因式时:
1) 如果常数项q是正数,那么它分解成两个 ,它们的符号与 的符号相同;
2) 如果常数项q是负数,那么它分解成两个 ,其中 与 的符号相同.
3) 对于分解的两个因数,还要看 是不是等于 .
5. 把一个多项式分解因式,一般可按如下步骤进行:
1) ;
2) ;
3) ;
4) .
口诀:一 二 三 四 五 六 .
6. 整式乘法是 ;而因式分解是 .
7. 分组分解法的关键是 ,先使因式分解能 进行,再使因式分解能在 进行,并且 .
第九章 分 式
1.
用A、B表示两个 ,A÷B可以表示成的![]() 形式.如果B中含有 ,式子
形式.如果B中含有 ,式子![]() 就叫做分式.A叫做 ,B叫做 .
就叫做分式.A叫做 ,B叫做 .
2. 和 统称有理式.
3. 在分式中,分母的值 .分式中的分母如果是 ,则分式没有意义.当 而
时,分式的值是零.
4. 分式的基本的性质:分式的分子与分母都
同一个 的整式,分式的值 .用式子表示是:
,
( ).
5. 分式的 、 与 的符号,改变其中 ,分式的值不变.
据此,分子或分母的系数是 时,一般先把 提到 的前边.
6. 分式约分:把分式的 与 分解因式,然后约去 .
7. 一个分式的 与 没有 时,叫做最简分式.
8. 分式乘以分式,用 ,
;
分式除以分式,把除式的 后与 相乘.
用式子表示为: , .
9. 根据 ,把几个异分母的分式分别化成与 的 的分式,叫做分式的通分.
10. 通分的最简公分母是指各分母 .
11. 同分母的分式相加减, , .
用式子表示是: .
12. 异分母的分式相加减,先 ,变为 ,然后再 .用式子表示是:
= = .
13. 叫做分式方程.
14. 在方程变形时,可能产生 的根,这种叫做原方程的 .故此分式方程必须 .
15. 解分式方程的一般步骤:
I. 在方程的两边都乘以 , ,化成 ;
II. 解这个 ;
III. 把 代入 ,看结果 ,使 的根是增根,必须 .
第十章 数的开方
1. 如果 ,这个数叫做a的平方根.
2. 求 的运算叫做开平方.它与 为互逆运算.
3. 一个正数有 个平方根,它们 ;
0有 个平方根,它是 ;
负数 平方根.
4.
一个 的正的平方根,用符号“ ”表示,它也叫做
. 负的平方根,用符号“ ”表示, 的平方根用符号表示“ ”.![]() .
.
5. 如果 ,这个数叫做a的立方根(也叫做 ).数a的立方根用符号“ ”表示,读作“ ”
6. 求 的运算,叫做开立方.它与 为互逆运算.
7. 正数有 的立方根,负数有 的立方根,0的立方根是 .
8. 如果正数的小数点向右或者向左移动2位,它的算术平方根的小数点就相应地 移动 位.
9. 被开方数的小数点向右或者向左每移动 位,它的立方根的小数点就相应地 移动 位.
10. *如果一个数的 ( )等于a,这个数叫做a的n次方根.换句话说,如果 ,那么x叫做a的n次方根.求 的运算,叫做把a开n次方根.a叫做 ,n叫做 .
11.
叫做a的n次算术根.零的n次方根也叫做 .即![]() .
.
12. ,叫做开方.开n次方根与 互为逆运算.
13. ,叫做无理数.
14. 和 统称实数.
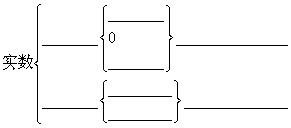
15. 和数轴上的点是一一对应关系.即
都可以用数轴上的一个点来表示,反过来,
.
16. 和 总可以进行开平方运算, 、 和 总可以进行开立方运算.
17. * 、 、 、 、
和 六种运算统称为代数运算.
第十一章 二次根式
1. 一般地,式子 ( ),叫做二次根式 .
2.
一般地,![]() 是一个 .
是一个 .
3.
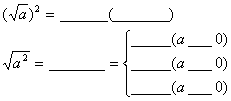
4. 积的算术平方根,等于 .用式子表示为: ( ) .
5.
二次根式的乘法用式子表示为:![]() .
.
6. 商的算术平方根等于 .用式子表示为 ( ) .
7. 二次根式的除法用式子表示为: .
8. ,叫做分母有理化.
9. 满足下列两个条件的二次根式,叫做二次最简根式:⑴ ;
⑵ .
10. 后,如果 相同,这几个二次根式叫做同类二次根式.
11. 两个含二次根式的代数相乘,如果它们的积 ,那么这两个代数式互为有理化因式.
12. *式子 满足下列条件时叫做根式.当n是奇数时,a可以是 ;当n是偶数时,a可以是 .
13. *根式基本性质:
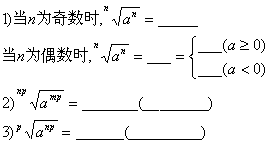
14. *根式的运算性质:
![]()
![]()
![]()
![]()
15. *如果一个根式适合下面三个条件:
⑴ ;
⑵ ;
⑶ . 这样的根式叫做最简根式.
16. *几个根式化为 后,如果 相同, 也相同,这几个根式叫做同类根式.
17. *根式的加减运算,就是先把根式化为 ,然后再 .
第十二章 一元二次方程
1. 方程的两边都是 的方程叫做整式方程.
2. 只含有 ,并且 的整式方程叫做一元二次方程.其一般形式为 .
3. 一元二次方程的基本解法有 、 、
和 .
4. 一元二次方程的求根公式: .
5. 把 叫做一元二次方程的根的判别式.
6. 一元二次方程 ,当Δ>0时, ;当Δ=0时, ;当Δ<0时 .反过来也 .
7.
如果方程![]() 的两个根是
的两个根是![]() ,那么
,那么![]() .
.
8.
如果方程![]() 的两个根是
的两个根是![]() ,那么
,那么![]() .
.
9.
以两个数![]() 为根的一元二次方程(二次项系数为1)是 .
为根的一元二次方程(二次项系数为1)是 .
10.
在分解二次三项式![]() 的因式时,可先求出方程
的因式时,可先求出方程![]() 的两个根
的两个根![]() ,然后写成 .
,然后写成 .
11. 的方程叫做无理方程.
12. 和 统称为有理方程.
13. *含有 个未知数,并且未知数的 的整式方程叫做高次方程.
14. 含有 ,并且 的整式方程是二元二次方程.
15. 解方程(组)的基本思想是:多元方程要“ ”,次数高的方程要“ ”,分式方程要“ ”和无理方程要“ ”,化为 方程.最后归结为解 方程 或 方程 .
16. 方程和 方程一定要检验.
第十三章 函数及其图象
1. 在平面内 ,组成平面直角坐标系.水平的数轴叫做 或 ,取 为正方向.铅直的数轴叫做 或 ,取 的为正方向,两轴交点O是 .这个平面叫做 .
2. 坐标平面内的点与 是一一对应.
3. 一般地,设在 过程中有 ,如果对于 , ,那么就说x是自变量,y是x的函数.
4. 函数的表示法: 、 、和 .
5. 用 (即 ) 表示函数的方法叫做解析法.
6. 一般地,对于一个函数,如果把自变量x与函数y的每对对应值分别作为 ,在坐标平面内 , 所组成的图形,就是这个函数的图象.画图象的步骤是① ,② ,③ .
7. 如果 ,那么y叫做x的一次函数.如果 ,那么y叫做x的正比例函数.
