一元二次方程练习题
班级 姓名
一、填空
1.一元二次方程![]() 化为一般形式为:
,二次项系数为: ,一次项系数为: ,常数项为: 。
化为一般形式为:
,二次项系数为: ,一次项系数为: ,常数项为: 。
2.关于x的方程![]() ,当
,当![]() 时为一元一次方程;当
时为一元一次方程;当![]() 时为一元二次方程。
时为一元二次方程。
3.已知直角三角形三边长为连续整数,则它的三边长是 。
4. ![]()
![]()
![]() ;
;![]()
![]()
![]() 。
。
5.直角三角形的两直角边是3︰4,而斜边的长是15㎝,那么这个三角形的面积是 。
6.若方程![]() 的两个根是
的两个根是![]() 和3,则
和3,则![]() 的值分别为
。
的值分别为
。
7.若代数式![]() 与
与![]() 的值互为相反数,则
的值互为相反数,则![]() 的值是 。
的值是 。
8.方程![]() 与
与![]() 的解相同,则
的解相同,则![]() = 。
= 。
9.当![]() 时,关于
时,关于![]() 的方程
的方程![]() 可用公式法求解。
可用公式法求解。
10.若实数![]() 满足
满足![]() ,则
,则![]() = 。
= 。
11.若![]() ,则
,则![]() = 。
= 。
12.已知![]() 的值是10,则代数式
的值是10,则代数式![]() 的值是 。
的值是 。
二、选择
1.要使分式![]() 的植为0,则
的植为0,则![]() 应该等于( )
应该等于( )
(A)4或1
(B)4
(C)1
(D)![]() 或
或![]()
2.若![]() 与
与![]() 互为倒数,则实数
互为倒数,则实数![]() 为( )
为( )
(A)±![]() (B)±1
(C)±
(B)±1
(C)±![]() (D)±
(D)±![]()
3.若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的根,且
的根,且![]() ≠0,则
≠0,则![]() 的值为( )
的值为( )
(A)![]() (B)1
(C)
(B)1
(C)![]() (D)
(D)![]()
4.关于![]() 的一元二次方程
的一元二次方程![]() 的两根中只有一个等于0,则下列条件正确的是( )
的两根中只有一个等于0,则下列条件正确的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.下列方程中,无论![]() 区和制,总是关于的一元二次方程的是( )
区和制,总是关于的一元二次方程的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6.某商品连续两次降价,每次都降20﹪后的价格为![]() 元,则原价是( )
元,则原价是( )
(A)![]() 元 (B)1.2
元 (B)1.2![]() 元 (C)
元 (C)![]() 元
(D)0.82
元
(D)0.82![]() 元
元
7.若方程![]()
![]() 中,
中,![]() 满足
满足![]() 和
和![]() ,则方程的根是( )
,则方程的根是( )
(A)1,0 (B)-1,0 (C)1,-1 (D)无法确定
8.方程![]() 的解的个数为( )
的解的个数为( )
(A)0 (B)1 (C)2 (D)1或2
9.关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则( )
有实数根,则( )
(A)![]() <0
(B)
<0
(B)![]() >0
(C)
>0
(C)![]() ≥0
(D)
≥0
(D)![]() ≤0
≤0
10.已知![]() 、
、![]() 是实数,若
是实数,若![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
(A)![]() 一定是0 (B)
一定是0 (B)![]() 一定是0 (C)
一定是0 (C)![]() 或
或![]() (D)
(D)![]() 且
且![]()
三、解方程
1. 选用合适的方法解下列方程
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
2.
解下列关于![]() 的方程
的方程
(1)![]() (2)
(2)![]()
四、解答
1. 如图,在正方形ABCD中,AB是4㎝,△BEC的面积是△DEF面积的4倍,则DE的长是多少?
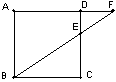
2.
已知等腰三角形底边长为8,腰长是方程![]() 的一个根,求这个三角形的面积。
的一个根,求这个三角形的面积。
3.
已知一元二次方程![]() 有一个根为零,求
有一个根为零,求![]() 的值。
的值。
4.
填写下表并探索一元二次方程![]() 的解的取值范围。
的解的取值范围。
|
| 8 | 6 | 4 | 2 | 0 | -2 |
|
|
从表中可以看出方程解应介于 和 之间。
5.
我们知道:对于任何实数![]() ,①∵
,①∵![]() ≥0,∴
≥0,∴![]() +1>0;②∵
+1>0;②∵![]() ≥0,∴
≥0,∴![]() +
+![]() >0.
>0.
模仿上述方法解答: 求证:(1)对于任何实数![]() ,均有:
,均有:![]() >0;(2)不论
>0;(2)不论![]() 为何实数,多项式
为何实数,多项式![]() 的值总大于
的值总大于![]() 的值。
的值。

6. 在△ABC中,AB=AC=8㎝,∠A=36°,BD平分∠ABC交AC于点D,求AD、CD的长。
五、列方程解应用题
1. 一个一元二次方程,其两根之和是5,两根之积是-14,求出这两个根。
2. 某工厂计划两年内把产量翻一番,如果每年比上一年提高的百分数相同,求这个百分数。
3. 用22长的铁丝,折成一个面积是30㎝2的矩形,求这个举行的长和宽。又问:能否折成面积是32㎝2的矩形呢?为什么?
4. 某科技公司研制成功一种产品,决定向银行贷款200万元资金用于生产这种产品,贷款的合同上约定两年到期时,一次性还本付息,利息为本金的8﹪。该产品投放市场后,由于产销对路,使公司在两年到期时除还清贷款的本息外,还盈余72万余。若该公司在生产期间每年比上一年资金增长的百分数相同,试求这个百分数。
5. 某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
某人购买了1000元债券,定期一年,到期兑换后他用去了440元,然后把剩下的钱又全部购买了这种债券,定期仍为一年,到期后他兑现得款624元。求这种债券的年利率。