安徽省2004年普通高中理科实验班招生考试
数 学 试 题
（满分150分，答题时间120分）
| 题 号 | 一 | 二 | 三 | 总 分 | |||
| 11 | 12 | 13 | 14 | ||||
| 得 分 | |||||||
| 得 分 | 评卷人 |
一、选择题（本题共5小题，每小题10分，满分50．每小
题均给出了代号为A、B、C、D的四个结论，其中只有一
个是正确的，请将正确答案的代号填在题后的括号内）
1．若
是方程
的根，则
的值为 ………【 】
A．0 B．1 C．－1 D．2
2．内角的度数为整数的正
边形的个数是 ………………………………【 】
A．24 B．22 C．20 D．18
3．某商场五一期间举行优惠销售活动，采取“满一百元送二十元，并且连环赠送”的
酬宾方式，即顾客每消费满100元（100元可以是现金，也可以是购物券，或二者
合计）就送20元购物券，满200元就送40元购物券，依次类推，现有一位顾客第
一次就用了16000元购物，并用所得购物券继续购物，那么他购回的商品大约相当
于它们原价的 ………………………………………………………………【 】
A．90% B．85% C．80% D．75%
4．设
为正整数，若
是完全平方数，则它前面的一个完全平方数是
【 】
A．
B．
C．
D．
5．横坐标、纵坐标都是整数的点叫做整点，函数
的图象上整点的个数
是 ……………………………………………………………………………【 】
A．3个 B．4个 C．6个 D．8个
| 得 分 | 评卷人 |
二、填空题（本题共5小题，每小题8分，共40分）
6．计算：1＋2－3＋4＋5－6＋7＋8－9＋…＋97＋98－99＋100＝ ．
7．已知实数满足
，则代数式
的值为
．
8．若方程组
的解为
且
＜3，则
的取值范围是
．
9．已知函数
的图象与轴有两个交点，且都在轴的负半
轴上，则
的取值范围是
．
10．如图，等腰梯形ABCD中，AB∥DC，∠A＝60°，AD＝DC＝10，点E，F分别
在AD，BC上，且AE＝4，BF＝，设四边形DEFC的面积为
，则关于的
函数关系式是 （不必写自变量的取值范围）．
 |
三、（本题共4小题，满分60分）
| 得 分 | 评卷人 |
11．（本题满分15分）
我们知道相交的两直线的交点个数是1，记两平行直线的交点个数是0；这样平面内的三条平行线它们的交点个数就是0，经过同一点的三直线它们的交点个数就是1；依次类推……
（1）请你画图说明同一平面内的五条直线最多有几个交点？
（2）平面内的五条直线可以有4个交点吗？如果有，请你画出符合条件的所有图形；如果没有，请说明理由．
（3）在平面内画出10条直线，使交点数恰好是31．
| 得 分 | 评卷人 |
12．（本题满分15分）
甲、乙两个粮库原来各存有整袋的粮食，如果从甲库调90袋到乙库，则乙库存粮是甲库的2倍；如果从乙库调若干袋到甲库，则甲库存粮是乙库的6倍．问甲库原来最少存粮多少袋？
| 得 分 | 评卷人 |
13．（本题满分15分）
⊙O1与⊙O2相交于点A、B，动点P在⊙O2上，且在⊙O1外，直线PA、PB分别
交⊙O1于点C、D．问：⊙O1的弦CD的长是否随点P的运动而发生变化？如果发生
变化，请你确定CD最长或最短时点P的位置；如果不发生变化，请给出你的证明．
 |
| 得 分 | 评卷人 |
14．（本题满分15分）
如图，函数
的图象交轴于M，交轴于N，点P是直线MN上任意一
点，PQ⊥轴，Q是垂足，设点Q的坐标为（
，0），△POQ的面积为S（当点P与M、N重合时，其面积记为0）．
（1）试求S与之间的函数关系式；
（2）在如图所示的直角坐标系内画出这个函数的图象，并利用图象求使得S＝
（＞0）的点P的个数．
 | |||
 | |||
安徽省2004年普通高中理科实验班招生考试
数学试题参考答案及评分标准
一、选择题（每小题10分，共50分）
1．C 2．B 3．C 4．D 5．B
二、填空题（每小题8分，共40分）
6．1684 7．7 8．－1＜＜5 9．＞－1且≠0
10．
三、解答题（每小题15分，共60分）
11．（本题满分15分）
解 （1）如图1，最多有10个交点； ……………………（4分）
 |  | ||
图1 图2
（2）可以有4个交点，有3种不同的情形，如图2． ……（10分）
（3）如图3所示． …………………（15分）
 |
图3
12．（本题满分15分）
解：设甲库原来存粮袋，乙库原来存粮
袋，依题意可得
． （1）
再设乙库调
袋到甲库，则甲库存粮是乙库的6倍，即
．
（2） ………………（5分）
由（1）式得
．
（3）
将（3）代入（2），并整理得
．
………………（10分）
由于
．
又、是正整数，从而有
≥1，即≥148；
并且7整除
，又因为4与7互质，所以7整除
．
经检验，可知的最小值为152．
答：甲库原来最少存粮153袋． …………………（15分）
13．当点P运动时，CD的长保持不变． …………………（4分）
证法一：A、B是⊙O1与⊙O2的交点，弦AB与点P的位置无关．……（6分）
连结AD，
∠ADP在⊙O1中所对的弦为AB，所以∠ADP为定值． ……………（10分）
∠P在⊙O2中所对的弦为AB，所以∠P为定值． ……………（12分）
因为∠CAD＝∠ADP＋∠P，
所以∠CAD为定值．
在⊙O1中∠CAD所对弦是CD，∴CD的长与点P的位置无关．………（15分）
证法二：在⊙O2上任取一点Q，使点Q在⊙O1外，设直线QA、QB分别交⊙O1
于C＇、D＇，连结C＇D＇．
∵ ∠1＝∠3，∠2＝∠3，∠1＝∠2，
|
|
∴ CC＇＝DD＇
∴ C＇mD＇＝CmD
∴ CD＝CD． …………………（15分）
 |
14．（本题满分15分）
解法1（1）① 当＜0时，OQ＝
，PQ＝
．
∴ S＝
；
② 当0＜＜4时，OQ＝，PQ＝．
∴ S＝
；
③ 当＞4时，OQ＝，PQ＝
．
∴ S＝
．
④ 当＝0或4时，S＝0．
于是，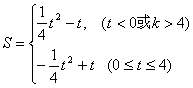
…………………………………………6分
（2）
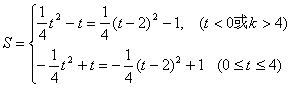
下图中的实线部分就是所画的函数图象． ……………………………………12分
 |
观察图象可知：
当0＜＜1时，符合条件的点P有四个；
当＝1时，符合条件的点P有三个；
当＞1时，符合条件的点P只有两个． ………………………………………15分
解法2：（1）∵ OQ＝
，PQ＝
，
∴ S＝
． ……………………………………4分
（2）
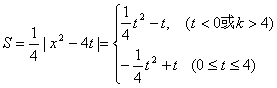………………………6分
以下同解法1．