初三数学第十二章过关试题
一、填空题
1、一元二次方程的一般形式为 当 时,它有两个实数根。
2、若x1、x2为一元二次方程ax2+bx+c=0(a≠0)的两个根,
则x1+x2= ,x1x2= ,![]() ,x12+x22=
,x12+x22=
3、以方程3x2-5x-11=0的两根的平方为根的整系数一元二次方程为
4、关于x的方程x2+(m2-2)x-3=0的一个根为1,则 m= 另一根等于
5、若关于x的方程x2-3x+m=0的两根差为5,则 m=
6、当x= 时,2x2-6x+4与x-1的值相等。
7、已知a、b是关于x的方程x2+(m+1)x+1=0(m<-1=的两个实数根,则
![]() =
,当m= 时,a=b.
=
,当m= 时,a=b.
8、关于x的方程x2-(m+7)x-6=0的根是2,则m=
9、已方程x2-3x+2=0的两根的倒数为根的整系数方程为
10、在实数范围内分解因式2x2-4x-3=
二、选择题:
1、关于x的方程(m+1)x2+2mx+m-1=0的根的情况是:( )
A、有不等的两个实数根 B、有相等的两个实数根 C、没有实数根
D、以上都不对
2、关于x的方程2x(mx-4)-x2+6=0没有实数根,则m的最小整数值是( )
A、-1 B、2 C、3 D、4
3、完成某项工作,甲需x天,乙需y天,甲、乙共同完成所需的天数是( )
A、x+y
B、![]() C、
C、![]() D、
D、![]()
4、方程(x+1)2=x+1的根是( )
A、0 B、-1 C、0或-1 D、2
5、方程(3-x)(x+7)=12 的根的情况( )
A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根
D、不能确定
6、已知方程组 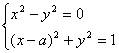 有两个相等的实数解,则
( )
有两个相等的实数解,则
( )
A、a=±1 B、a=±![]()
![]() C、a=
C、a=![]()
![]() D、a=-
D、a=-![]()
![]()
7、已知x 、y是实数,且(x2+y2)(x2-1+y2)=12,那么x2+y2的值是 ( )
A、4 B、-3或4 C、-3 D、3
8、已知一元二次方程 x2+Px+q=0的两个根分别为x1=3,x2=-4,则二次三项
x2-Px+q可分解为( )
A、 (x+3)(x-4) B、(x-3)(x+4) C、(x+3)(x+4) D、(x-3)(x-4)
三、解方程(组)
1、![]() 2、
2、
四、m取何值时,关于x的方程 2(m+1)x2+4mx+3m-2=0
(1)有两个相等的实数根?求出这两个根
(2)有一个根为零?求出另一个非零根
(3)两个实数根互为相反数?求出这两个根
选做题
一、填空:
1、已知关于x的方程(a2-1)x2-(a+1)x+1=0的两实数根互为倒数,则a=
2、当整数a= 时,(a-1)x2-(a2-2)x+a2+a=0的根都是整数。
二、选择:
1、已知关于x的方程2kx2+(8k+1)x=-8k有两个实数根,则k的取值范围( )
A、k>-![]() B、k≥-
B、k≥-![]() 且k≠0 C、k<-
且k≠0 C、k<-![]() D、k≤-
D、k≤-![]() 且k≠0
且k≠0
2、已知a、b、c是三角形ABC的三边且关于x的一元二次方程
(c-b)x2+2(b-a)x+(a-b)=0有两个相等实数根,则此三角形是( )
A、等要三角形 B、直角三角形 C、等边三角形 D、不等边三角形
三、关于x的一元二次方程x2-(m2+3)x+![]() (m2+2)=0
(m2+2)=0
1、试证无论m取何值实数方程总有两个正根。
2、设x1、x2为方程的两根且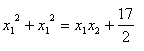 ,求m
,求m
四、x1、x2是关于x的方程x2-(2k+1)x+k2+1=0的两个实数根
1、若x1、x2都大于1,求实数k的取值范围
2、若![]()
![]() ,求k的值
,求k的值
答案:
一、填空题
1、ax2+bx+c=0(a≠0),b2-4ac≥0
2、-![]() ,
,![]() ,-
,-![]() ,
,![]()
3、9x2-9x+121=0
4、±2,-3
5、-4
6、1或5/2
7、![]() (m<-1), -3
(m<-1), -3
8、-8
9、2x2-3x+1=0
10、2(x-![]() )(x-
)(x-![]() )
)
二、选择题:
1、D 2、B 3、D 4、C 5、C 6、B 7、A 8、A
三、解方程
1、去分母两边都乘以2x2得
12-6x2=x(4-x)
整理得 5x2+4x-12=0
解得 x1=6/5,x2=-2
经检验:x1、x2都是方程的解
2、解:把![]() 看成是一元二次方程z2-7z+12=0的两根
看成是一元二次方程z2-7z+12=0的两根
解得:z1=3,z2=4
即:![]() 或
或![]()
解得;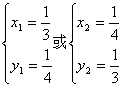
经检验得它们都是方程的解。
四、△=(4m)24×2(m+1)(3m-2)
=16m2-8(3m2+m-2)
=-8m2-8m+16
⑴要使方程有两个相等的实根须使△=0且2(m+1)≠0
即-8m2-8m+16=0且m≠-1
∴m2+m-2=0且m≠-1
解得:m1=-2,m2=1
当m1=-2时,方程变为x2+4x+4=0
解得x1=x2=-2
当m2=1时,方程变为4x2+4x+1=0
解得x3=x4=-1/2
⑵当一根为0时,3m-2=0
∴m=2/3
此时方程为10/3x2+8/3x=0解得x=-4/5
⑶当两实根互为相反数时有-![]()
∴m=0
此时方程为2x2-2=0
∴x1=1,x2=-1
选做题
一、填空:1、![]() 2、0或1
2、0或1
二、选择:1、B 2、A
三、1、证明:△=[-(m2+3)]2-4·![]() ·(m2+2)
·(m2+2)
=m4+6m2+9-2m2-4
=m4+4m2+5
=(m2+2)2+1
∵不论m为何值都有m2≥0而m2+2>0
∴(m2+2)2+1>0
∴△>0
又设两根为x1、x2,则x1+x2=m2+3>0 x1x2= (m2+2)>0
∴两根为正故无论为何实数方程总有两个正根
2、由韦达定理知x1+x2=m2+3 x1x2=![]() (m2+2)
(m2+2)
∴x12+x22-x1x2=(x1+x2)2-3x1x2
∴(m2+3)2-3·![]() ·(m2+2)=
·(m2+2)=![]()
∴ 2m4+9m2-5=0
∴m=±![]()
四、1、△=[-(2k+1)]2-4·(k2+1)=4k-3
∵方程有两个实数根
∴4k-3≥0 ∴k≥3/4
又x1+x2=2k+1 x1x2=k2+1
∴(x1-1)(x2-1)>0 ∴x1x2-(x1+x2)+1>0
∴(k2+1)-(2k+1)+1>0 即k2-2k+1>0
∴(k-1)2>0 当k≥3/4且k≠1时x1x2都大于1
2、当![]() 即x2=2x1时,有3x1=2k+1 ∴x1=
即x2=2x1时,有3x1=2k+1 ∴x1=![]()
又2x12=k2+1 ∴2·(![]() )2=k2+1
)2=k2+1
∴k2-8k+7=0
∴k=1,k=7