华中师大一附中2003年高一新生入学摸底测试
数 学 试 题
满分:150分 限时:120分钟 命题人:黄松生 2003.9.4
第I卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填在答题卡上.
1.在同一直角坐标系内,如果正比例函数y=mx与反比例函数y=![]() 的图象没有交点,那么m与p的关系一定是
的图象没有交点,那么m与p的关系一定是
A.m<0,p>0 B.m>0,p>0 C.mp<0 D.mp>0
2.在半径为5cm的圆中,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离是 A.7cm B.1cm C.5cm D.7cm或1cm
3.若点P(-1-2a,2a-4)关于原点对称的点在第一象限内,则a的整数解有
A.1个 B.2个 C.3个 D.4个
4.已知两圆半径分别为R和r(R>r),圆心距为d,且d2+R2-r2=2dR,那么两圆位置关系为
A.外切 B.内切 C.外离 D.外切或内切
5.已知x为实数,化简![]() 的结果为
的结果为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.已知关于x的方程2x2+x+m+![]() =0有两个不相等的负实根,则m的取值范围是
=0有两个不相等的负实根,则m的取值范围是
A.![]()
![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若α为直角三角形的一个锐角,则![]() 等于
等于
A.1–sinα–cosα B.1+sinα+cosα
C.0 D.sinα+cosα-1
![]() 8.已知点(-2,y1)、(-5
8.已知点(-2,y1)、(-5![]() ,y2)、(1
,y2)、(1![]() ,y3)在函数y=2x2+8x+7的图象上,则y1、y2、y3的大小关系是
,y3)在函数y=2x2+8x+7的图象上,则y1、y2、y3的大小关系是
A.y1>y2>y3 B.y2>y1>y3 C.y2>y3>y1 D.y3>y2>y1
9.已知sinα·cosα=![]() ,且0°<α<45°,则cosα-sinα的值为
,且0°<α<45°,则cosα-sinα的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在直角坐标系中,已知点A(-2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D、O、C为顶点的三角形与△AOB相似,这样的直线至多可以作
A.2条 B.3条 C.4条 D.6条
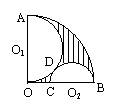 11.如图所示,已知扇形AOB的半径为12,OA⊥OB,C为OB上一点,
11.如图所示,已知扇形AOB的半径为12,OA⊥OB,C为OB上一点,
以OA为直径的半圆O1和以BC为直径的半圆O2相切于D,则图中阴影
部分的面积为
A.6π B.10π
C.12π D.20π
12.已知一元二次方程ax2+bx+c=0的两根之和为p,两根平方和为q,两根立方和为r,则ar+bq+cp的值是
A.-1 B.0 C.1 D.2
第I卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
 13.如图,AB为⊙O的直径,CD是⊙O的弦,
13.如图,AB为⊙O的直径,CD是⊙O的弦,
AB、CD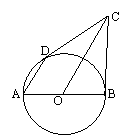 的延长线交于E点,已知AB=2DE,
的延长线交于E点,已知AB=2DE,
∠E=18°,则∠AOC的度数为__________.
14.如图,已知AB是⊙O的直径,BC是和⊙O相切于B
的切线,⊙O的弦AD平行于OC,若OA=2且AD+OC=6,
则CD=___________.
15.若规定两数a,b通过运算得4ab,即a*b=4ab,若x*x+2*x-2*4=0,则x=__________.
16.某县位于沙漠边缘地带,治理沙漠,绿化家乡是全县人民的共同愿望.到1998年底,全县沙漠的绿化率已达30%,此后,政府计划在近几年内,每年将当年年初未被绿化的沙漠面积的m%栽上树进行绿化,到2000年底,全县的沙漠绿化率已达到43.3%,则m的值等于_____________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)如图,已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,AD⊥PC于D,CE⊥AB于E,求证:
 (1)AD=AE
(1)AD=AE
(2)PC·CE=PA·BE
18.(本小题满分12分)已知![]() (a>b>0)是方程x2-5x+2=0的两个实根,求
(a>b>0)是方程x2-5x+2=0的两个实根,求![]() 的值.
的值.
19. (本小题满分12分)如图,△ABC中,AB=5,BC=6,BD=![]() BC,AD⊥BC于D,E为AB延长线上的一点,且EC交AD的延长线于F.
BC,AD⊥BC于D,E为AB延长线上的一点,且EC交AD的延长线于F.
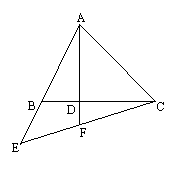 (1)设BE为x,DF为y,试用x的式子表示y.
(1)设BE为x,DF为y,试用x的式子表示y.
(2)当∠ACE=90°时,求此时x的值.
20. (本小题满分12分)通过电脑拨号上“因特网”的费用是由电话费和上网费两部分组成.以前我市通过“武汉热线”上“因特网”的费用为电话费0.18元/3分钟,上网费为7.2元/小时,后根据信息产业部调整“因特网”资费的要求,自1999年3月1日起,我市上”因特网“的费用调整为电话费0.22元/3分钟.上网费为每月不超过60小时,按4元/小时计算;超过60小时部分,按8元/小时计算.
(1)根据调整后的规定,将每月上“因特网”的费用y(元)表示为上网时间x(小时)的函数;
(2)资费调整前,网民聪聪在其家庭经济预算中,一直有一笔每月70小时的上网费用支出.“因特网”资费调整后,聪聪要想不超过其家庭经济预算中的上网费用支出,他现在每月至多可上网多少小时?
(3)从资费调整前后的角度分析,比较我市网民上网费用的支出情况.
21. (本小题满分12分)在直角坐标系xoy中,一次函数![]() 的图像与x轴、y轴分别交于点B和点A,点C的坐标是(0,1),点D在y轴上且满足∠BCD=∠ABD.求D点的坐标.
的图像与x轴、y轴分别交于点B和点A,点C的坐标是(0,1),点D在y轴上且满足∠BCD=∠ABD.求D点的坐标.
 |
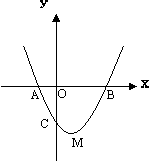
22. (本小题满分14分)如图,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等.直线y=3x-7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
(1)求这条抛物线的解析式;
(2)P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B、M重合),设OQ的长为t,四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围;
 (3)在线段BM上是否存在点N,使△NMC是等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由.
(3)在线段BM上是否存在点N,使△NMC是等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由.
数学试题参考答案
一、选择题
1.C 2.D 3.B 4.D 5.C 6.B 7.D 8.C 9.A
10.C 11.B 12.B
二、填空题
13.54° 14.![]() 15.2或-4 16.10
15.2或-4 16.10
三、解答题
17.证:(1)连AC、BC,∵PC是⊙O的切线,∴∠ABC=∠ACD,又∵AB为圆O的直径,
∴∠ACB=90°.又∵CE⊥AB.∴∠ABC=∠ACE,∴∠ACE=∠ACD,又AD⊥PC,AC公共边.
∴Rt△ACE≌Rt△ACD,∴CD=CE ,AD=AE.…………………………………………………(6分)
(2)在Rt△PCE和Rt△PAD中,∠CPE=∠APD,∴Rt△PCE∽Rt△PAD,∴![]() .又∵∠ABC=∠ACD,∴Rt△EBC∽Rt△DCA,∴
.又∵∠ABC=∠ACD,∴Rt△EBC∽Rt△DCA,∴![]() ,∴
,∴![]() .
.
∴![]() .…………………………………………………………………(12分)
.…………………………………………………………………(12分)
18.解:∵![]() 是方程
是方程![]() 的两实根,∴
的两实根,∴![]() .…………………………(4分)∴原式=
.…………………………(4分)∴原式=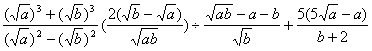 =
=
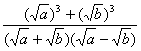
![]()
![]()
![]() ……………………………………………………………(12分)
……………………………………………………………(12分)
19.解:(1)过![]() 作
作![]() ∥
∥![]() 交
交![]() EC于
EC于![]() ,则△
,则△![]() ∽△
∽△![]() ,∴
,∴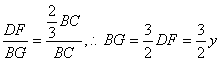 .…………………………………………………(3分)
.…………………………………………………(3分)![]() △
△![]() 中,可得
中,可得![]() ,又∵△
,又∵△![]() ∽△
∽△![]() ,∴
,∴ ………………………………………………………(6分)
………………………………………………………(6分)
(2)当∠![]() =90°时,则有∠
=90°时,则有∠![]() ∠
∠![]() ,∴
,∴![]() △
△![]() ∽
∽![]() △
△![]() ,
,
∴![]() ,∴
,∴![]() ,∴16=
,∴16=![]() .…………(10分)
.…………(10分)
代入![]() ,有
,有![]() ,解得
,解得![]() .………………………………………………………(12分)
.………………………………………………………(12分)
20.(1)![]()
![]() ………………………………………………(4分)
………………………………………………(4分)
(2)资费调整前,上网70小时所需费用为(3.6+7.2)×70=756元.资费调整后,若上网60小时,则所需费用为8.4×60=504(元).∵756>504,∴聪聪现在上网时间超过60小时.由![]() ,解得
,解得![]() .∴聪聪现在每月至多可上网约80.32小时.(7分)
.∴聪聪现在每月至多可上网约80.32小时.(7分)
(3)设调整前所需费用为![]() (元);调整后所需费用为
(元);调整后所需费用为![]() (元),则
(元),则![]()
当![]() 时,
时,![]() ,故
,故![]() .当
.当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() …………………………………………(11分)
…………………………………………(11分)
综上可得:当时,调整后所需费用少;
当![]() 时,调整前后所需费用相同;
时,调整前后所需费用相同;
当![]() 时,调整前所需费用少.………………………………………………(12分)
时,调整前所需费用少.………………………………………………(12分)
21.解:∵![]() 、
、![]() 是直线与
是直线与![]() 轴、
轴、![]() 轴的交点,令
轴的交点,令![]() ,解得
,解得![]() ,∴
,∴![]() ,令
,令![]() ,解得
,解得![]() .由勾股定理,
.由勾股定理,![]() .…………(2分)
.…………(2分)
(1)若![]() 点在
点在![]() 点上方时,则∠
点上方时,则∠![]() 为钝角,∵∠
为钝角,∵∠![]() ∠
∠![]() ,又∠
,又∠![]() =∠
=∠![]() ,∴△
,∴△![]() ∽△
∽△![]() ,∴
,∴![]() ,设
,设![]() ,则
,则![]() ,∵
,∵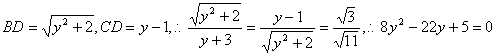 ,解得
,解得![]() 或
或![]() (舍去),∴点
(舍去),∴点![]() 的坐标为(0,
的坐标为(0,![]() )……………………………(6分)
)……………………………(6分)
(2)若![]() 点在
点在![]() 之间时,则∠
之间时,则∠![]() 为锐角,∵∠
为锐角,∵∠![]() =∠
=∠![]() ,又∠
,又∠![]() =∠
=∠![]() ,∴△
,∴△![]() ∽△
∽△![]() ,
,![]() ,设
,设![]() ,则-3<
,则-3<![]() <1,又
<1,又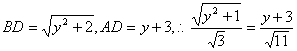 ,整理得
,整理得![]() ,解得
,解得![]() 或
或![]() (舍去),∴
(舍去),∴![]() 点坐标为(0,-
点坐标为(0,-![]() )…………………………(10分)
)…………………………(10分)
(3)若![]() 点在
点在![]() 点下方时,有∠
点下方时,有∠![]() ∠
∠![]() ∠
∠![]() >∠
>∠![]() ,又显然
,又显然
∠![]() <∠
<∠![]() ,∴
,∴![]() 点在
点在![]() 点下方是不可能的.…………………………………(11分)
点下方是不可能的.…………………………………(11分)
综上所述,![]() 点的坐标为(0,
点的坐标为(0,![]() )或(0,-
)或(0,-![]() )……………………………(12分)
)……………………………(12分)
22. (1)设这条抛物线的解析式为![]() 和
和![]() 时,
时,![]() 的值相等,∴
的值相等,∴![]() ,由抛物线的对称性,可知
,由抛物线的对称性,可知![]() 是这条抛物线的对称轴.又
是这条抛物线的对称轴.又![]() 与
与![]() 交于两点,且其中一点的横坐标为4,另一点是抛物线的顶点
交于两点,且其中一点的横坐标为4,另一点是抛物线的顶点![]() .∴点
.∴点![]() 的坐标为
的坐标为![]() ,直线与抛物线的另一交点为(4,5).∴
,直线与抛物线的另一交点为(4,5).∴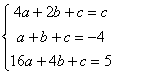
解得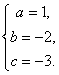 ∴这条抛物线的解析式为
∴这条抛物线的解析式为![]() …………………………(4分)
…………………………(4分)
(2)当![]() 时,即
时,即![]() 当
当![]() 时,
时,![]()
∴![]() 设直线
设直线![]() 的解析式为
的解析式为![]()
![]() ∴
∴![]() ,
,![]() ∴直线
∴直线![]() 的解析式为
的解析式为![]() ∵
∵![]() 轴于点
轴于点![]() ,又点
,又点![]() 在线段
在线段![]() 上,
上,![]() =6-2t
=6-2t
![]() △AOC+
△AOC+![]() =
=![]() (3+6-2
(3+6-2![]()
………………………………………………………………………………………………(8分)
(3)假设存在这样的点![]() ,使△
,使△![]() 为等腰三角形.∵点
为等腰三角形.∵点![]() 在
在![]() 上,不妨设
上,不妨设![]() 点坐标为
点坐标为![]() 则
则![]()
![]() △
△![]() 为等腰三角形,有以下三种可能:
为等腰三角形,有以下三种可能:
①若![]() ,则
,则![]() (舍去).
(舍去).![]()
∴![]()
![]() ②若
②若![]() 则
则![]()
∵![]() (舍去).∴
(舍去).∴![]()
③若![]() ,则
,则![]() 解得
解得![]()
∴![]() …………………………………………………………………………(13分)
…………………………………………………………………………(13分)
综上所述,存在这样的点![]() ,使△
,使△![]() 为等腰三角形.
为等腰三角形.
且点![]() 的坐标分别为
的坐标分别为![]() ……(14分)
……(14分)