九年级(上)单元测试卷
第一章 证明(二)
(时间90分钟 满分100分)
一、选择题(每小题3分，共30分)
1、△ABC中，AB=AC，BD平分ABC交AC边于点D，∠BDC=75°，则∠A的度数为（ ）
A、35° B、40° C、70° D、110°
2、如果一个三角形两边的垂直平分线的交点在第三边上，那么这个三角形是（ ）
A、锐角三角形 B、钝角三角形 C、直角三角形 D、以上都有可能
3、△ABC中，∠A∶∠B∶∠C=1∶2∶3，则BC∶AC∶AB=（ ）
A、1∶2∶3 B、 C、 D、
4、用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）正方形；（4）等腰三角形，一定可以拼成的图形是（ ）
A、（1）（2）（5） B、（2）（3）（5） C、（1）（4）（5） D、（1）（2）（3）
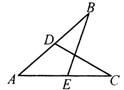
5、如图，D在AB上，E在AC上，且∠B＝∠C，那么补充下列一个条件后，仍无法判定△ABE≌△ACD的是（ ）．
A、AD＝AE B、∠AEB＝∠ADC C、BE＝CD D、AB＝AC
 | |||||
 | |||||
 | |||||
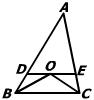
(第5题图) (第8题图) (第10题图)
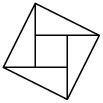
6、在△ABC中，AB=AC=3，BC=2，则S△ABC等于（ ）
A、3 B、2
C、2
D、3
7、若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的底角为（ ）
A、75°或15° B、30°或60° C、75° D、30°
8、如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD＝60°，BP＝1，CD＝
，则△ABC的边长为（ ）
A、3 B、4 C、5 D、6
9、两个顶角相等的等腰三角形框架，其中一个三角形框架的腰长为6，底边长为4，另一个三角形框架的底边长为2，则这个三角形框架的腰长为
A、6 B、4 C、3 D、2
10、某县政府准备为B、C两个村修建人畜饮水工程，取水点为A，已知AB=BC=AC，如图(1)、(2)、(3)的实线部分是三种不同的水管铺设线路设计方案，其中方案(3)的三段分别是∠BAC、∠ABC、∠BCA的平分线，设三种方案的水管长度分别是l1、l2、l3，则（ ）
A、l1>l2>l3 B、l2>l1>l3 C、l3>l2>l1 D、l1>l3>l2
二、填空题(每小题3分，共24分)
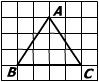
11、在方格纸上有一三角形ABC，它的顶点位置如图所示，则这个三角形是 三角形.
12、如图：△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件： ，使△AEH≌△CEB。
13、等腰直角三角形一条直角边的长为1cm，那么它斜边长上的高是 cm.
 |  |  | |||||
 | |||||||
(第11题图) (第12题图) (第17题图) (第18题图)
14、在△ABC和△ADC中，下列论断：①AB=AD；②∠BAC=∠DAC；③BC=DC，把其中两个论断作为条件，另一个论断作为结论，写出一个真命题：
15、补全“求作∠AOB的平分线”的作法：①在OA和OB上分别载取OD、OE，使OD=OE。②分别以D、E为圆心，以 为半径画弧，两弧在∠AOB内交于点C。③作射线OC即为∠AOB的平分线。
16、在△ABC中，边AB、BC、AC的垂直平分线相交于P，则PA、PB、PC的大小关系是
.
17、如图，△ABC中，AB=6cm，AC=5cm，BC=4cm，∠ABC与∠ACB的平分线相交于点O，过点O作DE∥BC交AB于点D，交AC于点E，则△ADE的周长等于 cm.
18、如图是2002年8月在北京召开的第24届国际数学家大会的会标，它是由4个相同的直角三角形拼和而成。若图中大小正方形的面积分别为52cm2和4cm2，则直角三角形的两条直角边的和是 cm.
三、(每小题6分，共12分)
19、如图所示，它是由6个面积为1的正方形组成的矩形，点A、B、C、D、E、F、G是小正方形的顶点，以这七个点中的任意三个为顶点，可组成多少个面积为1的三角形？请你写出所有这样的三角形.
20、已知：如图，△ABC中，AB=AC.
(1)按照下列要求画出图形：
①作∠BAC的平分线交BC于点D；
②过D作DE⊥AB，垂足为点E；
③过D作DF⊥AC，垂足为点F.
(2)根据上面所画的图形，求证：EB=FC.
四、(每小题6分，共18分)
21、已知：如图，△ABC是等边三角形，BD是AC边上的高，延长BC到E，使CE=BD.
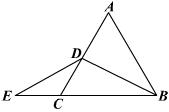求证：DB=DE
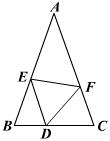22、如图，△ABC中，AB=AC，D、E、F分别在AB、BC、AC上，且BD=CE，∠DEF=∠B，图中是否存在和△BDE全等的三角形？并说明理由.
23、如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高.
求证：AD垂直平分EF.
五、(每小题8分，共16分)
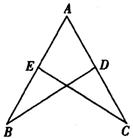24、此题有A、B、C三类题目，其中A类题4分，B类题6分，C类题8分．请你任选一类证明，多证明的题目不记分．
（A类）已知：如图，AB＝AC，AD＝AE．求证：∠B＝∠C．
（B类）已知：如图，CE⊥AB于点E，BD⊥AC于点D，BD、CE交于点O，且AO平分∠BAC．求证：OB＝OC．
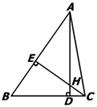
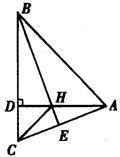（C类）如图9，△BDA、△HDC都是等腰直角三角形，且D在BC上，BH的延长线与 AC交于点E，请你在图中找出一对全等三角形，并写出证明过程．
25、已知：如图，△ABC（AB≠AC）中，D、E在BC上，且DE=EC，过D作DF//BA，交AE于点F，DF=AC.
求证：AE平分∠BAC.