优等生训练卷（9）

四、填空题（本大题有5小题，每小题4分，共20分）

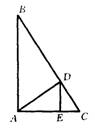27、如图，已知AD是Rt△ABC斜边BC上的高线，DE是Rt△ADC的斜边AC上的高线，如果DC：AD＝1：2，且S_△DCE=6，那么S_△ABC=_________

28、方程的解集是_________

29、在△ABC中，已知AB=AC，BD是∠ABC的角平分线，且BD=AD，那么∠A=_________

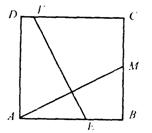30、如图，ABCD是正方形，M是BC的中点，将正方形折起，使点A与点M重合，设折痕为EF。若正方形的面积为64，那么△AEM的面积为_________

31、已知二次方程有且仅有一个根在–1与1之间，那么m的取值范围是_________

五、解答题（本大题有4小题，共40分）

32、（8分）一次函数的图像与二次函数的图像交于P，Q两点，如果以PQ为直径的圆恰好经过原点O，求m的值。

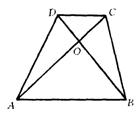33、（10分）如图，在梯形中，AB∥CD，对角线AC与BD相交于O，若，求的值。

34、（10分）如图，已知⊙O₂与⊙O₁相交于A，D两点，弦AC是⊙O₁的切线，弦AB是⊙O₂的切线。

（1）求证：AD是BD和DC的比例中项；

（2）延长BD交⊙O₂于E，延长CD交⊙O₁于F。求证：BE=CE；

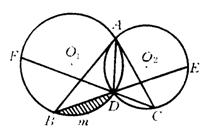（3）若⊙O₁的半径为10，∠C=45⁰，求弓形BmD的面积。

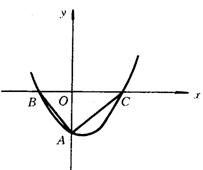
35、如图，已知函数的图象与y轴的交点为A，与x轴的交点为B，C（点C在点B的右侧）。

（1）求证：点B，C在y轴的两侧；

（2）求证：∠C为定值；

（3）当m为何值时，△ABC的面积最小，并求出此最小值。